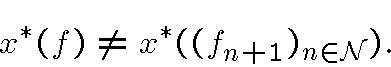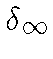 , значения которой равны
, значения которой равны 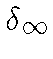 является чисто к.-а. мерой на
является чисто к.-а. мерой на 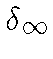 .
При этом
.
При этом
Следует отметить, что аналогичные конструкции можно построить на
семействе ![]() всех подмножеств натурального ряда
всех подмножеств натурального ряда ![]() . Именно,
рассмотрим полуалгебру
. Именно,
рассмотрим полуалгебру ![]() подмножеств
подмножеств ![]() , состоящую из
конечных и бесконечных промежутков
, состоящую из
конечных и бесконечных промежутков ![]() . Тогда функцию
. Тогда функцию
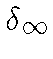 , значения которой равны
, значения которой равны ![]() на конечных и
на конечных и ![]() на бесконечных промежутках, можно, в некотором "аппроксимативном
смысле", трактовать как "равномерное" распределение на
на бесконечных промежутках, можно, в некотором "аппроксимативном
смысле", трактовать как "равномерное" распределение на ![]() .
Функция
.
Функция 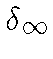 является чисто к.-а. мерой на
является чисто к.-а. мерой на ![]() и,
аналогично случаю отрезка
и,
аналогично случаю отрезка ![]() , можно указать чисто к.-а. меру
определенную на
, можно указать чисто к.-а. меру
определенную на ![]() и являющуюся продолжением
и являющуюся продолжением 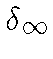 .
При этом
.
При этом
![\begin{displaymath}{\mathfrak B}\stackrel{\triangle}{=}\{\mu \in (add)_+[{\mathfrak N}] \mid (\mu \mid {\cal Z}) =
\delta_\infty\} =\end{displaymath}](img58.gif)
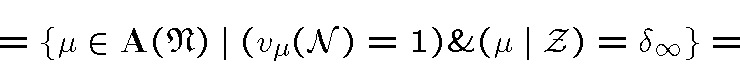
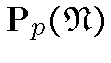 [множество всех чисто к.-а.
вероятностей на
[множество всех чисто к.-а.
вероятностей на 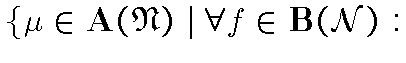
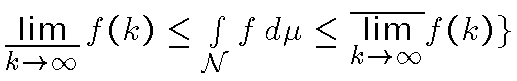
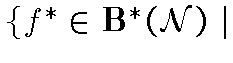
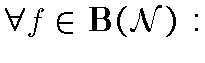
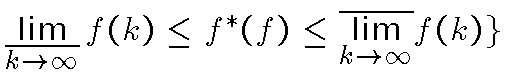 .
.
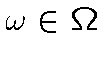 соответствует мера
соответствует мера
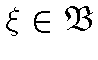 , такая, что
, такая, что
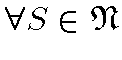 :
:
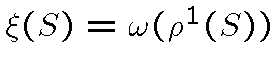 . Таким образом,
. Таким образом,
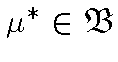 и
и
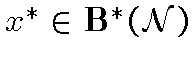 , причем
, причем
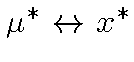 , то при
, то при
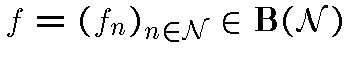 возможна ситуация
возможна ситуация