Построение
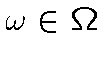 В дальнейших построениях будем использовать тот факт, что к.-а. меры
ограниченной вариации являются линейными непрерывными функционалами на (банаховом)
пространстве равномерных пределов ступенчатых функций.
Оснащая пространство всех
таких к.-а.
мер естественной сильной нормой (вариацией) пространства линейных непрерывных
функционалов на исходном банаховом пространстве, получаем пространство,
топологически сопряженное к исходному банаховому пространству. По теореме Алаоглу
всякое сильно
ограниченное и
В дальнейших построениях будем использовать тот факт, что к.-а. меры
ограниченной вариации являются линейными непрерывными функционалами на (банаховом)
пространстве равномерных пределов ступенчатых функций.
Оснащая пространство всех
таких к.-а.
мер естественной сильной нормой (вариацией) пространства линейных непрерывных
функционалов на исходном банаховом пространстве, получаем пространство,
топологически сопряженное к исходному банаховому пространству. По теореме Алаоглу
всякое сильно
ограниченное и 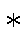 -слабо замкнутое множество в этом (сопряженном) пространстве
будет
-слабо замкнутое множество в этом (сопряженном) пространстве
будет 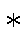 -слабо компактным. Возможность выделения из любой
направленности (и, в частности, из последовательности) в
компактном множестве сходящейся поднаправленности
является основой построения к.-а. вероятности, определенной на
семействе всех подмножеств промежутка
-слабо компактным. Возможность выделения из любой
направленности (и, в частности, из последовательности) в
компактном множестве сходящейся поднаправленности
является основой построения к.-а. вероятности, определенной на
семействе всех подмножеств промежутка 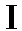 .
.
Пусть
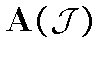 -- множество всех ограниченных
вещественнозначных (в/з) к.-а. мер на
-- множество всех ограниченных
вещественнозначных (в/з) к.-а. мер на 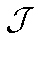 , а
, а
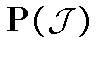 -- множество
всех к.-а. вероятностных мер на
-- множество
всех к.-а. вероятностных мер на 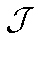 . Оснащаем
. Оснащаем
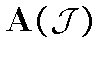
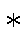 -слабой
топологией
-слабой
топологией
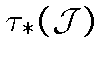 . В данном конкретном случае пространство
. В данном конкретном случае пространство
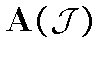 изометрически изоморфно пространству, топологически
сопряженному к пространству ограниченных в/з функций на
изометрически изоморфно пространству, топологически
сопряженному к пространству ограниченных в/з функций на
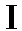 . Топологическое пространство
. Топологическое пространство
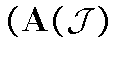 ,
,
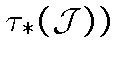 --
-- 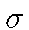 -компакт, а множество
-компакт, а множество
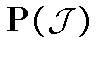 компактно в упомянутом ТП
(т.е.
компактно в упомянутом ТП
(т.е. 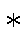 -слабо компактно) в силу теоремы Алаоглу. Это означает, в
частности, возможность изотонного "прореживания" произвольной
направленности в
-слабо компактно) в силу теоремы Алаоглу. Это означает, в
частности, возможность изотонного "прореживания" произвольной
направленности в
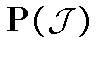 до сходящейся поднаправленности. В
качестве исходной направленности можно, в частности, использовать
последовательность.
до сходящейся поднаправленности. В
качестве исходной направленности можно, в частности, использовать
последовательность.
Если 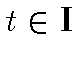 , обозначаем через
, обозначаем через 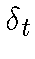 меру Дирака, сосредоточенную в точке
меру Дирака, сосредоточенную в точке 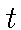 (и определенную
на
(и определенную
на 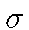 -алгебре
-алгебре 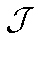 всех подмножеств
всех подмножеств 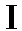 ). Кроме того,
полагаем
). Кроме того,
полагаем
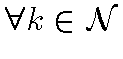 , где
, где
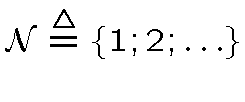 ,:
,:
Рассмотрим последовательность в компакте
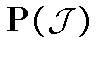 :
:
обладающую свойством:
где 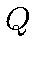 --
множество всех рациональных чисел из отрезка
--
множество всех рациональных чисел из отрезка ![$[0,1]$](img24.gif) .
В силу компактности
.
В силу компактности
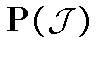 из данной последовательности можно
извлечь поднаправленность, сходящуюся к некоторой мере
из данной последовательности можно
извлечь поднаправленность, сходящуюся к некоторой мере
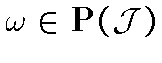 .
.
Устанавливается, что эта мера 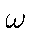 принадлежит множеству
принадлежит множеству 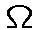 всех к.-а. вероятностей на
всех к.-а. вероятностей на 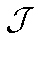 со свойствами
со свойствами
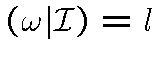 и
и 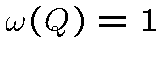 и является чисто к.-а. мерой в смысле разложения
Хьюитта-Иосида (то есть не имеет неотрицательных счетно-аддитивных
минорант, кроме тождественно равной нулю).
и является чисто к.-а. мерой в смысле разложения
Хьюитта-Иосида (то есть не имеет неотрицательных счетно-аддитивных
минорант, кроме тождественно равной нулю).


Next: Свойства множества
Up: НЕКОТОРЫЕ КОНЕЧНО-АДДИТИВНЫЕ ВЕРСИИ РАВНОМЕРНОГО
Previous: Постановка задачи
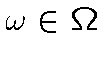 В дальнейших построениях будем использовать тот факт, что к.-а. меры
ограниченной вариации являются линейными непрерывными функционалами на (банаховом)
пространстве равномерных пределов ступенчатых функций.
Оснащая пространство всех
таких к.-а.
мер естественной сильной нормой (вариацией) пространства линейных непрерывных
функционалов на исходном банаховом пространстве, получаем пространство,
топологически сопряженное к исходному банаховому пространству. По теореме Алаоглу
всякое сильно
ограниченное и
В дальнейших построениях будем использовать тот факт, что к.-а. меры
ограниченной вариации являются линейными непрерывными функционалами на (банаховом)
пространстве равномерных пределов ступенчатых функций.
Оснащая пространство всех
таких к.-а.
мер естественной сильной нормой (вариацией) пространства линейных непрерывных
функционалов на исходном банаховом пространстве, получаем пространство,
топологически сопряженное к исходному банаховому пространству. По теореме Алаоглу
всякое сильно
ограниченное и 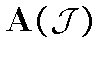 -- множество всех ограниченных
вещественнозначных (в/з) к.-а. мер на
-- множество всех ограниченных
вещественнозначных (в/з) к.-а. мер на 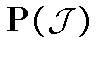 -- множество
всех к.-а. вероятностных мер на
-- множество
всех к.-а. вероятностных мер на 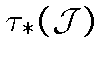 . В данном конкретном случае пространство
. В данном конкретном случае пространство
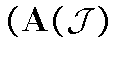 ,
,
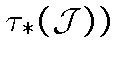 --
-- 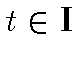 , обозначаем через
, обозначаем через 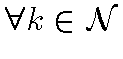 , где
, где
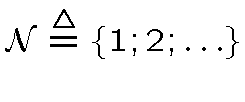 ,:
,:
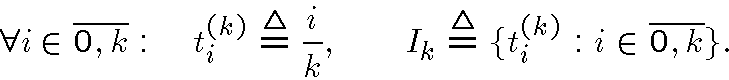
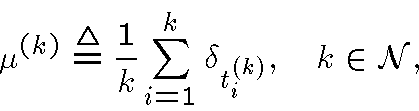
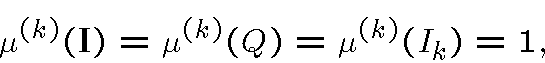
![$[0,1]$](img24.gif) .
В силу компактности
.
В силу компактности
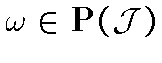 .
.
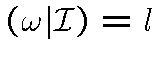 и
и 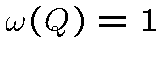 и является чисто к.-а. мерой в смысле разложения
Хьюитта-Иосида (то есть не имеет неотрицательных счетно-аддитивных
минорант, кроме тождественно равной нулю).
и является чисто к.-а. мерой в смысле разложения
Хьюитта-Иосида (то есть не имеет неотрицательных счетно-аддитивных
минорант, кроме тождественно равной нулю).