3. Набор математических формул

Вот теперь мы готовы! В этой главе мы встретимся с основной мощью TEX: математической версткой. Но имейте в виду, что эта глава дает только поверхностный обзор. Хотя для многих из вас изложенных здесь вещей будет достаточно, не отчаивайтесь, если вы не сможете найти решение, отвечающее нуждам верстки вашей математики. Весьма возможно, что ваша проблема решается в AMS-L^ATEX¹⁶ или в каком-нибудь ином пакете.

3.1 Общие сведения

L^ATEX включает в себя специальный режим для верстки математики.  . Математический текст внутри абзаца вводится между $\backslash$( и $\backslash$), между $ и $ или между \begin{math} или \end{math}. 

  Складывая $a$ в квадрате с 
  $b$ в квадрате, получаем 
  $c$ в квадрате. Или 
  излагая языком математики: 
  $c^{2}=a^{2}+b^{2}$

Складывая a в квадрате с b в квадрате, получаем c в квадрате. Или излагая языком математики: c²=a²+b²

  
  \TeX{} произносится как
  $\tau\epsilon\chi$.\\[6pt]
  100~м$^{3}$ воды.\\[6pt]
  Это исходит от моего 
  $\heartsuit$.

TEX произносится как $\tau\epsilon\chi$.

100 м³ воды.

Это исходит от моего $\heartsuit$.

Большие математические уравнения или формулы предпочтительнее <<выключать>>, то есть верстать их на отдельных строчках. Для этого заключайте их между $\backslash$[ и $\backslash$] или между \begin{displaymath} и \end{displaymath}. Это дает вам не нумерованные формулы. Если вы хотите, чтобы L^ATEX их нумеровал, пользуйтесь окружением equation.

  Складывая $a$ в квадрате с 
  $b$ в квадрате, получаем 
  $c$ в квадрате. Или 
  излагая языком математики: 
  \begin{displaymath}
    c^{2}=a^{2}+b^{2}
  \end{displaymath}
  И еще одна строчка

Складывая a в квадрате с b в квадрате, получаем c в квадрате. Или излагая языком математики:

c²=a²+b²

И еще одна строчка

При помощи $\backslash$label и $\backslash$ref вы можете в тексте ссылаться на уравнение.

  \begin{equation} 
    \label{eq:eps}
    \epsilon > 0
  \end{equation}
  Из (\ref{eq:eps}) 
  выводим \ldots

$$\epsilon > 0$$ (1)

Из (1) выводим ...

Заметьте, что выражения в выключных формулах верстаются в другом стиле:

  $\lim_{n \to \infty} 
  \sum_{k=1}^n \frac{1}{k^2} 
  = \frac{\pi^2}{6}$

$\lim_{n \to \infty} \sum_{k=1}^n \frac{1}{k^2} = \frac{\pi^2}{6}$

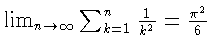
  \begin{displaymath}
    \lim_{n \to \infty} 
    \sum_{k=1}^n \frac{1}{k^2} 
    = \frac{\pi^2}{6}
  \end{displaymath}

$$\lim_{n \to \infty} \sum_{k=1}^n \frac{1}{k^2} = \frac{\pi^2}{6}$$

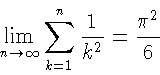
Математический режим отличается от текстового режима. Например, в математическом режиме:

1.

Большинство пробелов и возвратов каретки не принимаются во внимание, так как все пробелы либо выводятся из логики математических выражений, или должны в явном виде задаваться командами вроде $\backslash$,, $\backslash$quad или $\backslash$qquad.

2.

Пустые строчки недопустимы. Каждая формула занимает только один абзац.

3.

Каждая буква считается именем переменной, и верстается в этом качестве. Если вы хотите в формулу ввести нормальный текст (нормальный прямой шрифт с нормальными пробелами), то вам нужно вводить его командами \textrm{...}.

  \begin{equation}
    \forall x \in \mathbf{R}:
    \qquad x^{2} \geq 0
  \end{equation}

$$\forall x \in \mathbf{R}: \qquad x^{2} \geq 0$$ (2)

  

  \begin{equation}
    x^{2} \geq 0\qquad
    \textrm{для всех }x\in
    \mathbf{R}
  \end{equation}

$$x^{2} \geq 0\qquad \textrm{для всех }x\in \mathbf{R}$$ (3)

Математики бывают очень строги к используемым символам: здесь будет удобно использовать `ажурные полужирные символы' , которые получаются командой $\backslash$mathbb из пакетов amsfonts или amssymb. Последний пример теперь выглядит так:

  \begin{displaymath}
    x^{2} \geq 0\qquad
    \textrm{для всех }x\in
    \mathbb{R}
  \end{displaymath}

$$x^{2} \geq 0\qquad \textrm{для всех }x\in \mathbb{R}$$ (4)

3.2 Группировка в математическом режиме

Большинство команд математического режима действует только на следующий символ. Так что, если вы хотите, чтобы команда влияла на несколько символов, вам нужно сгруппировать их вместе при помощи фигурных скобок: {...}.

  \begin{equation}
    a^x+y \neq a^{x+y}
  \end{equation}

$$a^x+y \neq a^{x+y}$$ (5)

3.3 Составляющие математической формулы

В этом разделе будут описаны наиболее важные команды, используемые в математической верстке. Список всех доступных символов смотрите в разделе 3.9.

Строчные греческие буквы вводятся как \alpha, \beta, \gamma, ..., прописные буквы вводятся как \Gamma, \Delta, ...¹⁷

  $\lambda,\xi,\pi,\mu,%
  \Phi,\Omega$

$\lambda,\xi,\pi,\mu,% \Phi,\Omega$ Верхние и нижние индексы вводятся при помощи символов <<  ^ >> и <<_ >>.

  $a_{1}$ \qquad $x^{2}$ \qquad
  $e^{-\alpha t}$ \qquad
  $a^{3}_{ij}$\\
  $e^{x^2} \neq {e^x}^2$

a₁         x²          $e^{-\alpha t}$          a³_ij
$e^{x^2} \neq {e^x}^2$

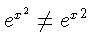
Квадратный корень  вводится как $\backslash$sqrt, корень n-ной степени печатается при помощи \sqrt[n]. Размер знака корня выбирается L^ATEX автоматически. Если нужен один только знак, используйте \surd.

  $\sqrt{x}$ \qquad 
  $\sqrt{ x^{2}+\sqrt{y} }$ 
  \qquad $\sqrt[3]{2}$\\[3pt]
  $\surd[x^2 + y^2]$

$\sqrt{x}$          $\sqrt{ x^{2}+\sqrt{y} }$          $\sqrt[3]{2}$
$\surd[x^2 + y^2]$

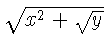
Команды $\backslash$overline и $\backslash$underline создают горизонтальные линии сразу над или под выражением.  

  $\overline{m+n}$

$\overline{m+n}$

Команды $\backslash$overbrace и $\backslash$underbrace создают длинные горизонтальные фигурные скобки сразу над или под выражением.  

  $\underbrace{ a+b+\cdots%
    +z }_{26}$

$\underbrace{ a+b+\cdots% +z }_{26}$

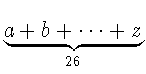
  Для добавления к переменным знаков математических акцентов, таких, как маленькие стрелки или знака тильда, вы можете пользоваться командами, перечисленным в таблице. Широкие <<шляпки>> и тильды, охватывающие несколько символов, генерируются командами $\backslash$widetilde и $\backslash$widehat. Символ <<' >> дает знак производной.  .

  
  \begin{displaymath}
    y=x^{2}\qquad y'=2x
    \qquad y''=2
  \end{displaymath}

$$y=x^{2}\qquad y'=2x \qquad y''=2$$

Векторы  часто указываются добавлением маленьких стрелок стрелки над переменной. Это делается командой $\backslash$vec. Для обозначения вектора от A до B полезны две команды $\backslash$overrightarrow и $\backslash$overleftarrow.

  \begin{displaymath}
    \vec a\quad
    \overrightarrow{AB}
  \end{displaymath}

$$\vec a\quad \overrightarrow{AB}$$

Имена функций типа $\lg$ часто верстаются прямым шрифтом, а не курсивом, как переменные. Поэтому L^ATEX содержит следующие команды для набора имен наиболее важных функций:  

\arccos   \cos    \csc   \exp   \ker     \limsup  \min   \sinh
\arcsin   \cosh   \deg   \gcd   \lg      \ln      \Pr    \sup
\arctan   \cot    \det   \hom   \lim     \log     \sec   \tan
\arg      \coth   \dim   \inf   \liminf  \max     \sin   \tanh

\[\lim_{x \rightarrow 0}
\frac{\sin x}{x}=1\]

$$\lim_{x \rightarrow 0} \frac{\sin x}{x}=1$$

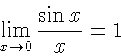
Для функции модуля функция модуля есть две команды: $\backslash$bmod для бинарного оператора <<$a \bmod b$>> и $\backslash$pmod для выражений вроде << $x\equiv a \pmod{b}$>>.

Двухъярусная дробь верстается командой $\backslash$frac{...}{...}. Часто предпочтительнее ее форма с косой чертой 1/2, потому что она смотрится лучше при небольшом количестве `дробного материала'.

  $1\frac{1}{2}$~часа
  \begin{displaymath}
    \frac{ x^{2} }{ k+1 }\qquad
    x^{ \frac{2}{k+1} }\qquad
    x^{ 1/2 }
  \end{displaymath}

$1\frac{1}{2}$ часа

$$\frac{ x^{2} }{ k+1 }\qquad x^{ \frac{2}{k+1} }\qquad x^{ 1/2 }$$

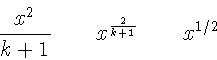
Для верстки биноминальных коэффициентов или аналогичных структур можно пользоваться или {... $\backslash$choose ...}, или {... $\backslash$atop ...}. Вторая команда дает тот же вывод, что и первая, но без скобок.

\begin{displaymath}
{n \choose k}\qquad {x \atop y+2}
\end{displaymath}

$${n \choose k}\qquad {x \atop y+2}$$

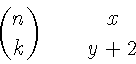
Оператор интеграла  печатает команда  $\backslash$int, оператор суммы  -- команда  $\backslash$sum. Верхние и нижние пределы указываются при помощи знаков <<^>> и <<_>>, так же, как верхние и нижние индексы.

\begin{displaymath}
\sum_{i=1}^{n} \qquad
\int_{0}^{\frac{\pi}{2}} \qquad
\end{displaymath}

$$\sum_{i=1}^{n} \qquad \int_{0}^{\frac{\pi}{2}} \qquad$$

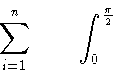
Для  скобок и прочих ограничителей  в TEX существует множество символов (скажем, $[\;\langle\;\Vert\;\updownarrow$). Круглые и квадратные скобки можно вводить соответствующими клавишами, фигурные скобки --\{, прочие ограничители -- специальными командами (например, \updownarrow). Список доступных ограничителей смотрите в таблице.

\begin{displaymath}
{a,b,c}\neq\{a,b,c\}
\end{displaymath}

$${a,b,c}\neq\{a,b,c\}$$

Если вы поместите перед открывающим ограничителем команду $\backslash$left, или перед закрывающим -- $\backslash$right, то TEX автоматически выберет правильный размер ограничителя. Заметьте, что вы должны каждый $\backslash$left закрывать соответствующим $\backslash$right. Если вы не хотите ничего справа, используйте невидимый ограничитель $\backslash$right..

\begin{displaymath}
1 + \left( \frac{1}{ 1-x^{2} }
    \right) ^3
\end{displaymath}

$$1 + \left( \frac{1}{ 1-x^{2} } \right) ^3$$

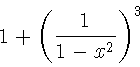
В некоторых случаях необходимо указать корректный размер математического ограничителя  вручную, для этого есть команды $\backslash$big, $\backslash$Big, $\backslash$bigg и $\backslash$Bigg, служащие префиксами к большинству команд ограничителей¹⁸.

$\Big( (x+1) (x-1) \Big) ^{2}$\\
$\big(\Big(\bigg(\Bigg($\quad
$\big\}\Big\}\bigg\}\Bigg\}$\quad
$\big\|\Big\|\bigg\|\Bigg\|$

$\Big( (x+1) (x-1) \Big) ^{2}$
$\big(\Big(\bigg(\Bigg($     $\big\}\Big\}\bigg\}\Bigg\}$     $\big\Vert\Big\Vert\bigg\Vert\Bigg\Vert$

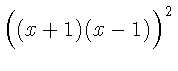
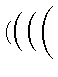
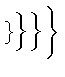
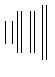
Чтобы ввести в формулу три точки, есть несколько команд. $\backslash$ldots верстает точки на базовой линии, $\backslash$cdots -- центрированные. Кроме того, существуют команды $\backslash$vdots для вертикальных и $\backslash$ddots для диагональных точек.    В разделе 3.5 вы найдете другой пример.

\begin{displaymath}
x_{1},\ldots,x_{n} \qquad
x_{1}+\cdots+x_{n}
\end{displaymath}

$$x_{1},\ldots,x_{n} \qquad x_{1}+\cdots+x_{n}$$

3.4 Математические пробелы

  Если выбранные TEX пробелы внутри формул неудовлетворительны, вы можете их подстраивать с использованием команд управления пробелами. Команды для маленьких пробелов: $\backslash$, для $\frac{3}{18}\:\textrm{\Eng quad}$ (0.166em), $\backslash$: для $\frac{4}{18}\: \textrm{\Eng quad}$ (0.222em) и $\backslash$; для $\frac{5}{18}\: \textrm{\Eng quad}$ (0.277em). Экранированный символ пробела \ дает средних размелов пробел, а $\backslash$quad (1em) и $\backslash$qquad (2em) дают большие пробелы. Размер $\backslash$quad примерно соответствует ширине буквы `M' в текущем шрифте. Команда \! $\backslash$"! производит отрицательный пробел размером $-\frac{3}{18}\:\textrm{\Eng quad}$ (0.166em).

\newcommand{\ud}{\mathrm{d}}
\begin{displaymath}
\int\!\!\!\int_{D} g(x,y)
  \, \ud x\, \ud y 
\end{displaymath}
вместо
\begin{displaymath}
\int\int_{D} g(x,y)\ud x \ud y
\end{displaymath}

$$\int\!\!\!\int_{D} g(x,y) \, \mathrm{d}x\, \mathrm{d}y$$

вместо

$$\int\int_{D} g(x,y)\mathrm{d}x \mathrm{d}y$$

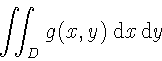
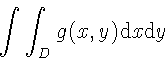
Заметьте, что `d' в дифференциале обычно верстается прямым шрифтом.

   
3.5 Вертикально расположенный материал

Для верстки матриц пользуйтесь окружением array. Его работа напоминает окружение tabular. Для разрыва строки используется команда \\.

\begin{displaymath}
\mathbf{X} =
\left( \begin{array}{ccc}
x_{11} & x_{12} & \ldots \\
x_{21} & x_{22} & \ldots \\
\vdots & \vdots & \ddots
\end{array} \right)
\end{displaymath}

$$\mathbf{X} = \left( \begin{array}{ccc} x_{11} & x_{12} & \ldo... ...{22} & \ldots \\ \vdots & \vdots & \ddots \end{array} \right)$$

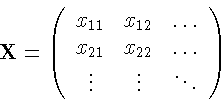
Окружение array можно также использовать для верстки выражений, имеющих один большой ограничитель, подставляя <<.>> в качестве невидимого правого ограничителя:

\begin{displaymath}
y = \left\{ \begin{array}{ll}
 a & \textrm{если $d>c$}\\
 b+x & \textrm{по утрам}\\
 l & \textrm{остальное время дня}
  \end{array} \right.
\end{displaymath}

$$y = \left\{ \begin{array}{ll} a & \textrm{если $d>c$ }\\ b... ...рам}\\ l & \textrm{остальное время дня} \end{array} \right.$$

Для формул, занимающих несколько строк или для систем уравнений  вместо equation пользуйтесь окружениями eqnarray и eqnarray*. В eqnarray каждая строка получает отдельный номер уравнения. В eqnarray* номера не ставятся.

Окружения eqnarray и eqnarray* работают наподобие таблицы из трех столбцов формата {rcl}, где средний столбец используется для знака равенства, или знака неравенства, или другого подходящего знака. Команда \\ разбивает строки.

\begin{eqnarray}
f(x) & = & \cos x     \\
f'(x) & = & -\sin x   \\
\int_{0}^{x} f(y)dy &
 = & \sin x
\end{eqnarray}

$$\cos x$$ f(x) = (6)

$$-\sin x$$ f'(x) = (7)

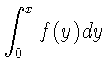$$\int_{0}^{x} f(y)dy \sin x$$ = (8)

Заметьте, что по обеим сторонам средней колонки, знаков равенства, слишком много свободного места. Оно может быть уменьшено установкой \setlength\arraycolsep{2pt}, как в следующем примере.

  Длинные уравнения не будут автоматически разбиваться на правильные части. Автор должен указать, где их разбивать и насколько выравнивать. Чаще всего для этого используют следующие методы:

\setlength\arraycolsep{2pt}
\begin{eqnarray}
\sin x & = & x -\frac{x^{3}}{3!}
     +\frac{x^{5}}{5!}-{}
                    \nonumber\\
 & & {}-\frac{x^{7}}{7!}+{}\cdots
\end{eqnarray}}

$$\sin x x -\frac{x^{3}}{3!} +\frac{x^{5}}{5!}-{}$$ =

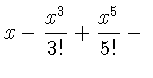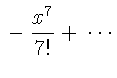$${}-\frac{x^{7}}{7!}+{}\cdots$$ (9)

\begin{eqnarray}
\lefteqn{ \cos x = 1
     -\frac{x^{2}}{2!} +{} }
                    \nonumber\\
 & & {}+\frac{x^{4}}{4!}
     -\frac{x^{6}}{6!}+{}\cdots
\end{eqnarray}

$${ \cos x = 1 -\frac{x^{2}}{2!} +{} }$$

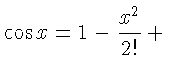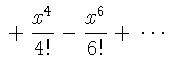$${}+\frac{x^{4}}{4!} -\frac{x^{6}}{6!}+{}\cdots$$ (10)

Команда $\backslash$nonumber заставляет L^ATEX не генерировать номер для этого уравнения.

Такими методами может быть сложно получить правильно выглядящие вертикально выровненные уравнения; более мощную альтернативу предоставляет пакет amsmath.

3.6 Размер математического шрифта

  В математическом режиме TEX выбирает размер шрифта в зависимости от контекста. Индексы, например, верстаются меньшим шрифтом. Если вы хотите добавить к уравнению обычный текст командой \textrm, механизм переключения размера работать не будет, так как \textrm временно выходит в текстовый режим. Чтобы оставить его работающим, используйте команду \mathrm¹⁹. Но имейте в виду, $\backslash$mathrm будет хорошо работать только с короткими элементами. Пробелы по-прежнему не активны и акцентированные символы не работают²⁰.

\begin{equation}
2^\textrm{nd} \quad 
2^\mathrm{nd}
\end{equation}

$$2^\textrm{\Eng nd} \quad 2^\mathrm{nd}$$ (11)

Все же иногда вам нужно указать L^ATEX корректный размер шрифта. В математическом режиме размер устанавливается четырьмя командами:

$\backslash$displaystyle ( $$123$$), $\backslash$textstyle ( $123$), $\backslash$scriptstyle ( $123$) и $\backslash$scriptscriptstyle ( $123$).

Смена стилей влияет также на способ изображения пределов.

\begin{displaymath}
\mathop{\mathrm{corr}}(X,Y)= 
 \frac{\displaystyle 
   \sum_{i=1}^n(x_i-\overline x)
   (y_i-\overline y)} 
  {\displaystyle\biggl[
 \sum_{i=1}^n(x_i-\overline x)^2
\sum_{i=1}^n(y_i-\overline y)^2
\biggr]^{1/2}}
\end{displaymath}

$$\mathop{\mathrm{corr}}(X,Y)= \frac{\displaystyle \sum_{i=... ...-\overline x)^2 \sum_{i=1}^n(y_i-\overline y)^2 \biggr]^{1/2}}$$

Это один из примеров, когда нам нужны скобки большие, чем предоставляемые стандартными \left[ \right].

3.7 Теоремы, законы, ...

При написании математических документов, вам, вероятно, нужен способ верстки <<лемм>>, <<определений>>, <<аксиом>> и аналогичных структур. L^ATEX поддерживает это командами

$\backslash$newtheorem{название}[счетчик]{ текст}[раздел] Аргумент название -- это краткое ключевое слово, используемое для идентификации <<теоремы>>. Аргументом текст вы определяете настоящее название <<теоремы>>, под которым она будет печататься в документе.

Аргументы в квадратных скобках необязательны. Оба они используются для определения того, как нумеровать <<теорему>>. Аргументом счетчик вы может указать название предварительно объявленной <<теоремы>>. Новая <<теорема>> будет тогда нумероваться в той же последовательности. Аргумент раздел позволяет вам указать раздел, внутри которого вы хотите нумеровать вашу <<теорему>>.

После использования в преамбуле документа команды $\backslash$newtheorem, вы можете пользоваться следующими командами:

\begin{название}[текст]
Это интересная теорема.
\end{название}

На этом теории должно быть достаточно. Дальнейшие примеры должны развеять последнюю тень сомнений, и окончательно убедить вас, что окружение \newtheorem слишком сложно, чтобы его можно было понять:

% определения для 
% преамбулы документа
\newtheorem{law}{Law}
\newtheorem{jury}[law]{Jury}
% в теле документа
\begin{law} \label{law:box}
Don't hide in the witness box
\end{law}
\begin{jury}[The Twelve]
It could be you! So beware and
see law \ref{law:box}\end{jury}
\begin{law}No, No, No\end{law}

Law 1   Don't hide in the witness box

Jury 2 (The Twelve)   It could be you! So beware and see law 1

Law 3   No, No, No

Теорема <<Jury>> использует тот же счетчик, что и теорема <<Law>>. Следовательно, она получит номер в последовательности с другими теоремами <<Law>>. Аргумент в квадратных скобках указывает заголовок теоремы, или нечто аналогичное.

\flushleft
\newtheorem{mur}{Murphy}[subsection]
\begin{mur}
Если существует два или
более способа сделать
нечто, и один их этих
способов может привести
к катастрофе, то кто-то
обязательно это сделает.
\end{mur}

Murphy 3.7.1   Если существует два или более способа сделать нечто, и один их этих способов может привести к катастрофе, то кто-то обязательно это сделает.

Теорема <<Murphy>> получает номер, связанный с номером текущего раздела. Вы можете также использовать другую структурную единицу, например, главу или подраздел.

   
3.8 Полужирные символы

В L^ATEX довольно непросто получить жирные символы; это, вероятно, сделано преднамеренно, потому что непрофессионалы слишком часто злоупотребляют ими. Команда смены шрифта \mathbf дает полужирные символы, но они обычные (прямые), тогда как математические символы обычно курсивные. Существует команда $\backslash$boldmath, но она может использоваться только вне математического режима. То же относится и к символам.

\begin{displaymath}
\mu, M \qquad \mathbf{M} \qquad
\mbox{\boldmath $\mu, M$}
\end{displaymath}

$$\mu, M \qquad \mathbf{M} \qquad \mbox{\boldmath$\mu, M$ }$$

Заметьте, что запятая тоже полужирная, что может быть нежелательным.

Пакет amsbsy (включаемый пакетом amsmath) включает команду $\backslash$boldsymbol, и команду <<полужирного для бедных>> $\backslash$pmb²¹, которая использует двухпроходную печать в системах без шрифтов, требуемых для полужирных символов.

\begin{displaymath}
\mu, M \qquad
\boldsymbol{\mu}, \boldsymbol{M}
\qquad \pmb{\mu}, \pmb{M}
\end{displaymath}

$$\mu, M \qquad \boldsymbol{\mu}, \boldsymbol{M} \qquad \pmb{\mu}, \pmb{M}$$

   
3.9 Список математических символов

В следующих таблицах вы найдете все символы, известные обычно в математическом режиме.

Для доступа к символам, перечисленным в таблицах²² в преамбуле документа должен быть загружен пакет amssymb, и в системе должны быть установлены математические шрифты AMS. Если пакеты и шрифты AMS в вашей системе не установлены, посмотрите на
CTAN:macros/latex/packages/amslatex

  

Таб.: Акценты математического режима

 

Таб.: Строчные греческие буквы

 

Таб.: Прописные греческие буквы

 

Таб.: Бинарные отношения

 

Таб.: Бинарные операторы

 

Таб.: Большие операторы

 

Таб.: Стрелки

  

Таб.: Ограничители

 

Таб.: Большие ограничители

 

Таб.: Прочие символы

 

Таб.: Не-математические символы

  

Таб.: Ограничители AMS

 

Таб.: Буквы греческого и иврита AMS

 

Таб.: Бинарные отношения AMS

 

Таб.: Стрелки AMS

  

Таб.: Отрицательные бинарные отношения и стрелки AMS

 

Таб.: Бинарные операторы AMS

 

Таб.: Прочие символы AMS

 

Таб.: Математические алфавиты