![$\displaystyle \begin{array}{c c} 0 & 1 [2mm] 0 & 0 \\
\end{array}$](img112.gif) ![$\displaystyle \begin{array}{c c} -0.3 & -0.1 [2mm] -0.2 & -0.4 \\
\end{array}$](img115.gif) ![$\displaystyle \begin{array}{c} 0 [2mm] 0.333 \\
\end{array}$](img118.gif) |
(11.1) |
This section contains three case studies of control system
design and analysis using Time-Delay System Toolbox.
Case study 1: Model 2-dimensional system,
Case study 2: Combustion stability in liquid propellant rocket motors,
Case study 3:
Wind tunnel model.
Consider 2-dimensional system with delay [33]
hence
![$\displaystyle \begin{array}{c c} 0 & 1 [2mm] 0 & 0 \\
\end{array}$](img112.gif)
![$\displaystyle \begin{array}{c c} -0.3 & -0.1 [2mm] -0.2 & -0.4 \\
\end{array}$](img115.gif)
![$\displaystyle \begin{array}{c} 0 [2mm] 0.333 \\
\end{array}$](img118.gif)
Open-loop system (11.1) is unstable because it has two
open-loop roots with positive real parts:
![]() = 0.198±0.323 i. Figure 1 and Figure 2 show the simulation results
by stepd and impulsed for the open-loop system.
= 0.198±0.323 i. Figure 1 and Figure 2 show the simulation results
by stepd and impulsed for the open-loop system.
Let us take the weight matrices as
where
A)
Take
![]() = 1.
We can find, using functions lqdelay, the matrices
= 1.
We can find, using functions lqdelay, the matrices
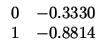
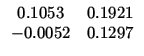
Thus to system (11.1) and the weight matrices
(11.3) (with
![]() = 1) corresponds the
control
= 1) corresponds the
control
![$\displaystyle \begin{array}{c c}
0 & 1 [2mm] -0.333 & -0.8814 \\
\end{array}$](img147.gif)
![$\displaystyle \begin{array}{c c} -0.3 & -0.1 [2mm] -0.2 & -0.4 \\
\end{array}$](img115.gif)
B)
Take
![]() = 10.
We can find, using functions lqdelay, the matrices
= 10.
We can find, using functions lqdelay, the matrices
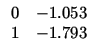

![$\displaystyle \begin{array}{c c}
0 & 1 [2mm] -1.0530 & -1.7930 \\
\end{array}$](img163.gif)
![$\displaystyle \begin{array}{c c} -0.3 & -0.1 [2mm] -0.2 & -0.4 \\
\end{array}$](img115.gif)
A linearized version of the feed system and combustion chamber equations, assuming nonsteady flow, are given by 5
Here
![]() (t) = fractional variation of pressure in the
combustion chamber,
(t) = fractional variation of pressure in the
combustion chamber,
t is the unit of time normalized with gas residence
time, ![]() , in steady operation,
, in steady operation,
![]() = value of time lag in steady operation,
= value of time lag in steady operation,
![]() = pressure in combustion chamber in steady
operation,
= pressure in combustion chamber in steady
operation,
![]() = const for some number
= const for some number
![]() ,
,
![]() =
= ![]() ,
,
![]() (t) = fractional variation of injection and
burning rate,
(t) = fractional variation of injection and
burning rate,
![]() (t) = relative variation of p1,
(t) = relative variation of p1,
=1cm p1 = instantaneous pressure at that place in the feeding line where the capacitance representing the elasticity is located,
![]() = fractional length for the constant pressure
supply,
= fractional length for the constant pressure
supply,
J = inertial parameter of the line,
P = pressure drop parameter,
![]() (t) = fractional variation of instantaneous mass
flow upstream of the capacitance,
(t) = fractional variation of instantaneous mass
flow upstream of the capacitance,
![]() p = injector pressure drop in steady operation,
p = injector pressure drop in steady operation,
p0 = regulated gas pressure for constant pressure
supply,
E = elasticity parameter of the line.
For our purpose we have taken
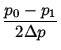
This gives, for
x(t) = (![]() (t),
(t),![]() (t),
(t),![]() (t),
(t),![]() (t))',
(t))',
The system (11.9) has two roots with positive
real part:
![]() = 0.11255±1.52015 i.
= 0.11255±1.52015 i.
Let us take the weight matrices as
Using function lqdelay we can find the matrices


Thus to system (11.9) with the weight matrices (11.10) corresponds LQR control
![$\scriptstyle ^{\left[\begin{array}{c c c c}
-0.2 & 0.0398 & -1 & 0 \\
0 & -...
...
0 & 0.2332 & -1 & -1 \\
0 & -1.1198 & 1 & 0
\end{array}\right] \times S }$](img219.gif)

The corresponding closed-loop system has the form
![$\displaystyle \begin{array}{c c c c}
\gamma - 1 & 0 & 0 & 0 [2mm]
0.0398 ...
... & -1.1198 [2mm]
-1 & 0 & -1 & 1 [2mm]
0 & 1 & -1 & 0 \end{array}$](img221.gif)
![$\displaystyle \begin{array}{c c c c}
- \gamma & 0 & 1 & 0 [2mm]
0 & 0 & 0 & 0 [2mm]
0 & 0 & 0 & 0 [2mm]
0 & 0 & 0 & 0 \end{array}$](img224.gif)
![$\displaystyle \begin{array}{c c c c}
0 & 0 & 0 & 0 [2mm]
0 & -1 & 0 & 0 [2mm]
0 & 0 & 0 & 0 [2mm]
0 & 0 & 0 & 0 \end{array}$](img227.gif)
Using functions of Toolbox one can check that solutions of the closed-loop systems tend to zero (see Figure 5).
Solutions of the optimal closed-loop system corresponding to
![]() = 0.95 and
= 0.95 and
![]() = 0.87 one can see on Figure 6.
= 0.87 one can see on Figure 6.
A linearized model of the high-speed closed-air unit wind tunnel is [26,27]
with
a = ![]() ,
k = - 0.117, w = 6,
,
k = - 0.117, w = 6, ![]() = 0.8,
= 0.8,
![]() = 0.33s.
= 0.33s.
The state variable x1, x2, x3 represent
deviations from a chosen operating point
(equilibrium point) of the following quantities:
x1 = Mach number,
x2 = actuator position guide vane angle in a
driving fan,
x3 = actuator rate.
The delay represents the time of the transport
between the fan and the test section.
The system can be written in matrix form
where![$\displaystyle \begin{array}{c c c }
- a & 0 & 0 [2mm]
0 & 0 & 1 [2mm]
0 & -\omega^2 & -2 \xi \omega
\end{array}$](img238.gif)
![$\displaystyle \begin{array}{c c c }
0 & a k & 0 [2mm]
0 & 0 & 0 [2mm]
0 & 0 & 0
\end{array}$](img241.gif)
Let us take the weight matrices as
Using function lqdelay we can find the matrices
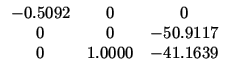
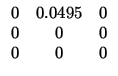
Thus to system (11.13) and the weight matrices (11.14) corresponds LQR control
![$\scriptstyle ^{\left[\begin{array}{c c c}
-0.5092 & 0 & 0 \\
0 & 0 & -50.9117 \\
0 & 1.0000 & -41.1639
\end{array}\right] \times S }$](img261.gif)
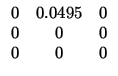
The corresponding closed-loop system has the form
![$\displaystyle \begin{array}{c c c}
-0.5092 & 0 & 0 [2mm]
0 & 0 & 1.0000 [2mm]
0 & -50.9117 & -41.1639 \end{array}$](img263.gif)
![$\displaystyle \begin{array}{c c c}
0 & 0.0596 & 0 [2mm]
0 & 0 & 0 [2mm]
0 & 0 & 0 \end{array}$](img266.gif)
![$\displaystyle \begin{array}{c c c c}
0 & 0 & 0 [2mm]
0 & 0 & 0 [2mm]
0 & 0 & -1296 \end{array}$](img269.gif)
Using functions of Toolbox one can check that solutions of the closed-loop systems tend to zero (see Figure 7).