Рассматриваются вопросы лексикографической двойственности для задач линейного и квадратичного программирования. Проблема формулируется так: как поставить исходную задачу лексикографической оптимизации, чтобы двойственная задача допускала лексикографическое прочтение, при этом чтобы эта пара объектов была связана математически содержательными соотношениями. В статье поставленный вопрос решается для линейных и квадратичных задач оптимизации.
Под двойственной задачей к задаче МП
О п р е д е л е н и е. Задача C называется собственной, если C и C* разрешимы и их оптимальные значения совпадают. В противном случае задача C называется несобственной (НЗ).
В частности, если ограничения задачи C несовместны
(противоречивы), то ![]() несобственная. Задача аппроксимации
(коррекции) несобственной модели C, т.е. поиск разрешимой модели,
``ближайшей'' к C, может быть поставлена, в частности, следующим
образом. Пусть
несобственная. Задача аппроксимации
(коррекции) несобственной модели C, т.е. поиск разрешимой модели,
``ближайшей'' к C, может быть поставлена, в частности, следующим
образом. Пусть
![]() - параметрический класс задач,
поглощающий C, т.е.
- параметрический класс задач,
поглощающий C, т.е.
![]() при некотором
при некотором
![]() . Положим
. Положим
![]() собственная}. Если
собственная}. Если
![]() функция качества коррекции, то задача оптимальной коррекции может быть
записана так:
функция качества коррекции, то задача оптимальной коррекции может быть
записана так:
П р и м е р. Пусть
![]()
![]() . В качестве
. В качестве
![]() можно
выбрать, например,
можно
выбрать, например,
![]() . Если
. Если
![]() оптимальный
вектор задачи коррекции по критерию
оптимальный
вектор задачи коррекции по критерию
![]() , то модель
, то модель
![]() выступает в качестве
модели компромисса. Понятно, что если C разрешима и
регулярна, то
выступает в качестве
модели компромисса. Понятно, что если C разрешима и
регулярна, то
![]() .
.
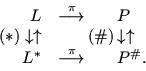
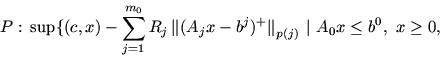
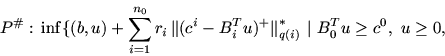
При минимальных требованиях к конструкции этих задач имеет место
Теорема (двойственности) [1]. Пусть подсистемы
![]() ,
, ![]() и
и
![]() ,
, ![]() совместны, а параметры Rj и ri выбраны из
условий:
совместны, а параметры Rj и ri выбраны из
условий:
Для большого числа частных реализаций задач P и P# условия теоремы выполняются автоматически. Приведем два примера таких случаев:
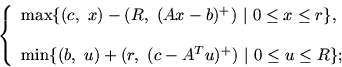
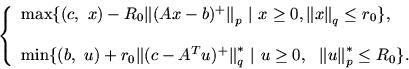
Пусть в C функции
{fj(x)}m0 дифференцируемы. Выше были
определены отображения ![]() и (#). Дополним их отображением
(l), заключающимся в линеаризации задачи в точке p. Приведем
общую схему двойственности для нелинейного программирования:
и (#). Дополним их отображением
(l), заключающимся в линеаризации задачи в точке p. Приведем
общую схему двойственности для нелинейного программирования:
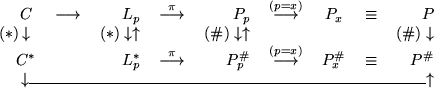
Приведем вид задач P и P# для C, получающихся в силу
изображенной схемы. Пусть ![]() матрица частных производных
функций
{fj(x)}1m, bx=Axx-F(x), где
FT(x)=[f1(x),..., fm(x)],
матрица частных производных
функций
{fj(x)}1m, bx=Axx-F(x), где
FT(x)=[f1(x),..., fm(x)],
![]() ;
FT(x)=[F0(x),...,
Fm0(x)]; Ajx, Bix, bjx, cix
(j=0,..., m0;
;
FT(x)=[F0(x),...,
Fm0(x)]; Ajx, Bix, bjx, cix
(j=0,..., m0;
![]() разбиения матрицы Ax и
векторов bx, cx на фрагменты по аналогии разбиений матрицы A
и векторов b, c на фрагменты Aj, Bi и bj, ci.
Тогда:
разбиения матрицы Ax и
векторов bx, cx на фрагменты по аналогии разбиений матрицы A
и векторов b, c на фрагменты Aj, Bi и bj, ci.
Тогда:
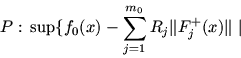
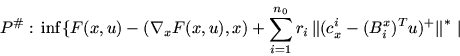
В предположениях выпуклости задачи C и дифференцируемости ее определяющих функций имеет место аналог теоремы двойственности из п. 1.3.
Симметричная двойственность для лексикографической задачи линейного программирования - это двойственность для такой постановки задачи ЛП, когда в качестве двойственного объекта выступает также лексикографическая задача ЛП, при этом эти задачи связаны математически содержательными регулярными соотношениями.
Пусть
![]() Rk.
Лексикографический порядок
Rk.
Лексикографический порядок
![]() в Rk,
отвечающий упорядочению индексов координат
p=(i1 ,..., ik),
определяется следующим образом:
в Rk,
отвечающий упорядочению индексов координат
p=(i1 ,..., ik),
определяется следующим образом:
![]() , если
первая пара несовпадающих координат с номером it удовлетворяет
неравенству
, если
первая пара несовпадающих координат с номером it удовлетворяет
неравенству
![]() ; совпадение всех координат
соответствует равенству z=z'. Этот порядок естественным образом
определяет экстремальные элементы на том или ином множестве
; совпадение всех координат
соответствует равенству z=z'. Этот порядок естественным образом
определяет экстремальные элементы на том или ином множестве ![]() Rk. Например, элемент
Rk. Например, элемент
![]() лексикографически максимален
лексикографически максимален
(l-максимальный) на Z, если из
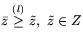 вытекает
вытекает
![]() . Аналогично определяется лексикографически
минимальный элемент. Заметим, что лексикографический экстремум
связан с экстремумом в последовательном программировании, а именно:
l-максимальный элемент
. Аналогично определяется лексикографически
минимальный элемент. Заметим, что лексикографический экстремум
связан с экстремумом в последовательном программировании, а именно:
l-максимальный элемент
![]() это оптимальный вектор
заключительной из последовательности задач:
это оптимальный вектор
заключительной из последовательности задач:
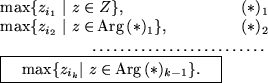
Здесь Arg...![]() оптимальное множество обозначенной
вслед задачи.
оптимальное множество обозначенной
вслед задачи.
В основе построения первого варианта лексикографической
двойственности (l-двойственности) лежит соответствие каркасов
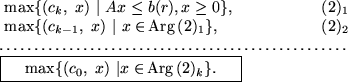
Лексикографически двойственную к Lp(r) задачу
поставим в форме:
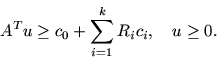
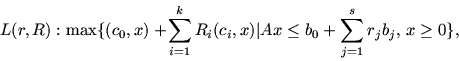
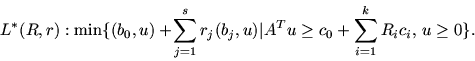
Четыре введенные для рассмотрения задачи, а именно:
Lp(r) и Lq(l)(R), L(r, R) и
![]() связаны между собой важными свойствами,
которые и составляют содержание двойственности для
лексикографической постановки задачи линейного
программирования.
связаны между собой важными свойствами,
которые и составляют содержание двойственности для
лексикографической постановки задачи линейного
программирования.
Лемма 2.1. Пусть задача ЛП
Д о к а з а т е л ь с т в о. Пусть
![]() совокупность вершин многогранника
совокупность вершин многогранника ![]() системы
системы
![]() . Ранг ее совпадает с
размерностью пространства переменной u, поэтому по крайней
мере одна вершина этого многогранника существует. В качестве
. Ранг ее совпадает с
размерностью пространства переменной u, поэтому по крайней
мере одна вершина этого многогранника существует. В качестве
![]() можно взять
можно взять
![]() , где
, где ![]() -я координата вектора pk. Вектором
-я координата вектора pk. Вектором ![]() будет
будет
![]() . Смысл этой конструкции
понятен: в качестве решения задачи
. Смысл этой конструкции
понятен: в качестве решения задачи ![]() независимо от
реализации вектора b выступает одна из вершин многогранника
независимо от
реализации вектора b выступает одна из вершин многогранника
![]() . Поэтому выбор
. Поэтому выбор ![]() по нашему правилу (с
запасом ``прочности'') обеспечивает, независимо от b,
непустоту рассматриваемого пересечения.
по нашему правилу (с
запасом ``прочности'') обеспечивает, независимо от b,
непустоту рассматриваемого пересечения.
Лемма 2.2. Для разрешимой задачи
последовательного программирования
| (2.1) |
| (2.2) |
Д о к а з а т е л ь с т в о.
Дело в том [2], что выбор R1 осуществляется из условия:
![]() , где
, где
![]() двойственная
оценка неравенства
двойственная
оценка неравенства
![]() в задаче
в задаче
| (2.3) |
Обобщением содержания лемм 2.1 и 2.2 (с учетом их доказательств) может служить
Лемма 2.3. Если задача Lp(r)
разрешима, то существует не пустая область конструктивно
определяемых значений параметра
R=[R1,..., Rk] таких,
что
![\begin{displaymath}
\begin{array}{c}
\mbox{Arg}\ L_p(r)=\mbox {Arg}\,\max \{(c_...
...i,\ x)\ \vert \\ [8pt]
Ax\leq b(r),\ \ x\geq0\},
\end{array} \end{displaymath}](img473.gif) |
(2.4) |
Д о к а з а т е л ь с т в о этой леммы состоит в последовательном применении двух предыдущих лемм.
Лемма 2.4. Пусть в задачах Lp(r) и
![]() ,
q=(js,..., j1, 0).
При условии совместности их систем ограничений
необходимым и достаточным условием разрешимости задач
Lp(r) и Lq(l)(R) является выполнимость соотношений:
,
q=(js,..., j1, 0).
При условии совместности их систем ограничений
необходимым и достаточным условием разрешимости задач
Lp(r) и Lq(l)(R) является выполнимость соотношений:
![\begin{displaymath}
\begin{array}{c}
c_{i_{\scriptstyle t}} \in {\mbox{cone}}
...
...h {$\mathrm{R}$}}}_n^{+}\\ [4pt]
(t=0,1,..., k);
\end{array} \end{displaymath}](img475.gif) |
(2.5) |
![\begin{displaymath}
\begin{array}{c}
b_{j_{\scriptstyle l}} \in {\mbox{cone}}
...
...h {$\mathrm{R}$}}}_m^{+}\\ [4pt]
(l=0, 1,...,s),
\end{array} \end{displaymath}](img476.gif) |
(2.6) |
Содержание этой леммы состоит в переформулировке
применительно к рассматриваемой ситуации условия
разрешимости обычной задачи ЛП, например, в
форме
![]()
![]() , а
именно: при непустоте ее допустимого множества (т.е. при
совместности ее системы ограничений) разрешимость
эквивалентна выполнимости соотношения
, а
именно: при непустоте ее допустимого множества (т.е. при
совместности ее системы ограничений) разрешимость
эквивалентна выполнимости соотношения
![]() , что, в свою очередь, эквивалентно
разрешимости системы
, что, в свою очередь, эквивалентно
разрешимости системы
![]() . Понятно, что
получение условий (2.5), (2.6) требует последовательного
применения выписанного соотношения.
. Понятно, что
получение условий (2.5), (2.6) требует последовательного
применения выписанного соотношения.
Теорема 2.1. Если задачи
![]() ,
, ![]() (i=0,..., k; j=0,..., s) разрешимы, то существует
непустая область конструктивно определяемых значений
параметров
(i=0,..., k; j=0,..., s) разрешимы, то существует
непустая область конструктивно определяемых значений
параметров ![]() и
и ![]() таких, что
таких, что
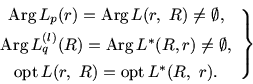 |
(2.7) |
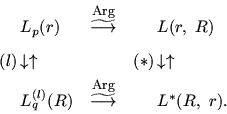
В этой схеме ![]() символ отображения в
лексикографически двойственную задачу,
символ отображения в
лексикографически двойственную задачу, ![]() символ
отображения в классически двойственную задачу,
символ
отображения в классически двойственную задачу,
![]() означает переход к
эквивалентной задаче в смысле наследования (сохранения)
оптимального множества.
означает переход к
эквивалентной задаче в смысле наследования (сохранения)
оптимального множества.
З а м е ч а н и я к формулировке теоремы.
1. Задачи ![]() и
и
![]() являются
взаимно двойственными (в классическом смысле), поэтому их
оптимальные значения совпадают
являются
взаимно двойственными (в классическом смысле), поэтому их
оптимальные значения совпадают![]() в этом смысле 3-е
соотношение в (2.7) приведено для полноты.
в этом смысле 3-е
соотношение в (2.7) приведено для полноты.
2. Предположение о разрешимости задач {Lji}
влечет разрешимость систем ограничений в задачах ![]() и
и
![]() при любых
при любых ![]() ,
, ![]() . Действительно, если
. Действительно, если
![]() допустимый вектор для
Lji,
допустимый вектор для
Lji, ![]() допустимый вектор для
допустимый вектор для
![]() (его существование вытекает из теоремы
двойственности), то векторы
(его существование вытекает из теоремы
двойственности), то векторы
![]() и
и
![]() будут допустимыми для
будут допустимыми для ![]() и
и
![]() , что и обеспечивает их разрешимость.
, что и обеспечивает их разрешимость.
Пояснение к доказательству теоремы. По лемме 2.3
можно обеспечить выбор ![]() , при
котором будет выполняться первое из соотношений (2.7)
, при
котором будет выполняться первое из соотношений (2.7)![]() каково бы ни было
каково бы ни было ![]() . С другой стороны, по этой же
лемме можно обеспечить выбор
. С другой стороны, по этой же
лемме можно обеспечить выбор ![]() , при котором
справедливо второе соотношение из (2.7)
, при котором
справедливо второе соотношение из (2.7)![]() каково бы ни
было
каково бы ни
было ![]() . Значения
. Значения ![]() и
и ![]() и будут
необходимыми значениями параметров R и r,
обеспечивающими справедливость теоремы 2.1.
и будут
необходимыми значениями параметров R и r,
обеспечивающими справедливость теоремы 2.1.
Конструктивизм нахождения ![]() и
и ![]() вскрывается доказательством леммы 2.
вскрывается доказательством леммы 2.
З а м е ч а н и е. Можно было бы показать,
что множества значений ![]() и
и ![]() , для которых
справедлива теорема, являются конусами (не замкнутыми).
, для которых
справедлива теорема, являются конусами (не замкнутыми).
Ниже мы рассмотрим задачу ЛП в обычной постановке, но с
акцентом на упорядочение (по ``важности'') ограничений как в
прямой задаче L, так и в двойственной ![]() . Такая
постановка определяет однозначный выбор максимально
совместных подсистем (МСП) в их системах ограничений. Пусть
. Такая
постановка определяет однозначный выбор максимально
совместных подсистем (МСП) в их системах ограничений. Пусть
Для определенности будем считать p=(1,..., m),
q=(1,..., n). МСП формируются путем наращивания числа
неравенств, начиная с конца (включение условия ![]() в
МСП производим автоматически). При таком наращивании
возможны перескоки, т.е. ситуации, когда включение
очередного неравенства ведет к несовместности, однако
включение вместо него последующего неравенства дает
совместную подсистему. Таких перескоков может быть
несколько. На допущение таких перескоков при образовании МСП
можно смотреть как на исправление (пересмотр) первоначальной
упорядоченности ограничений (по ``важности'').
в
МСП производим автоматически). При таком наращивании
возможны перескоки, т.е. ситуации, когда включение
очередного неравенства ведет к несовместности, однако
включение вместо него последующего неравенства дает
совместную подсистему. Таких перескоков может быть
несколько. На допущение таких перескоков при образовании МСП
можно смотреть как на исправление (пересмотр) первоначальной
упорядоченности ограничений (по ``важности'').
Чтобы не усложнять нумерацию при выделении МСП, будем
считать, что перескоков нет. Выпишем таким образом
выделенные МСП:
| (3.1) |
| (3.2) |
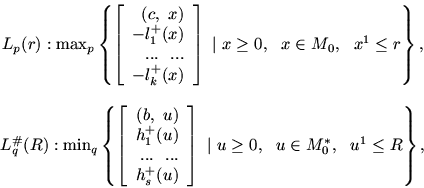
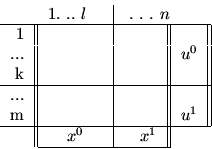
Заметим, что вхождение ограничений ![]() и
и
![]() в задачах Lp(r) и Lq# требуется
существом дела.
в задачах Lp(r) и Lq# требуется
существом дела.
Скаляризация задачи Lp с помощью вектора R и
задачи Lq# - с помощью вектора r приводит к
паре задач:
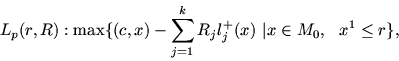
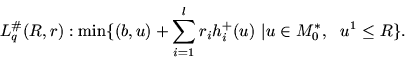
Задачи Lp(r, R) и Lq#(R, r) связаны утверждением [I]:
Если R и r выбраны так, что
Нижеследующая теорема (с учетом сформулированного утверждения) дает связь между задачами Lp, Lq#, Lp(r, R) и Lq#(R, r).
Теорема 3.1. Существует непустая
область конструктивно определяемых параметров ![]() и
и
![]() таких, что
таких, что
З а м е ч а н и е. Если задача L разрешима
(тогда разрешима и ![]() ), то задачи Lp(r) и
), то задачи Lp(r) и
![]() совпадают с L, а задачи Lq#(R) и
совпадают с L, а задачи Lq#(R) и
![]() совпадают с
совпадают с ![]() . Так что теорема
3.1 формулируется специально для неразрешимых задач линейного
программирования, в которых ограничения упорядочены (со
смыслом упорядочения ``по важности'').
. Так что теорема
3.1 формулируется специально для неразрешимых задач линейного
программирования, в которых ограничения упорядочены (со
смыслом упорядочения ``по важности'').
Пусть P и ![]() задачи из п. 1.
задачи из п. 1.
Важным является вопрос об аппроксимационном смысле
задач P и P# по отношению к L и ![]() .
Ниже этот смысл будет раскрыт через термины
лексикографической оптимизации.
.
Ниже этот смысл будет раскрыт через термины
лексикографической оптимизации.
Будем исходить (в содержательном плане) из того, что системы
ограничений задач L и ![]() разбиты на подсистемы
разбиты на подсистемы ![]() (j=1,..., m0) и
(j=1,..., m0) и
![]() (i=1,..., n0), причем
неравенства из одной подсистемы не ранжируются, а сами подсистемы
ранжируются, например, в соответствии с такими упорядочениями:
(0,
m0,..., 1) и
(0, n0,..., 1). Введенному упорядочению можно
придать следующий смысл: ограничения
(i=1,..., n0), причем
неравенства из одной подсистемы не ранжируются, а сами подсистемы
ранжируются, например, в соответствии с такими упорядочениями:
(0,
m0,..., 1) и
(0, n0,..., 1). Введенному упорядочению можно
придать следующий смысл: ограничения ![]() ,
, ![]() и
и
![]() ,
, ![]() носят директивный характер и
предполагаются совместными, остальные
носят директивный характер и
предполагаются совместными, остальные![]() факультативными (в
целом же они могут быть несовместными). Однако в силу
введенной упорядоченности подсистем функции
факультативными (в
целом же они могут быть несовместными). Однако в силу
введенной упорядоченности подсистем функции
![]() (j=1,...,m0);
(j=1,...,m0);
![]() (i=1,..., n0), играющие роль невязок
соответствующих подсистем, должно минимизировать последовательным
образом в соответствии с упорядочениями
p=(m0,..., 1) и
q=(n0,..., 1). Как уже было отмечено в предыдущих параграфах, это
эквивалентно постановке следующих двух задач лексикографической
оптимизации:
(i=1,..., n0), играющие роль невязок
соответствующих подсистем, должно минимизировать последовательным
образом в соответствии с упорядочениями
p=(m0,..., 1) и
q=(n0,..., 1). Как уже было отмечено в предыдущих параграфах, это
эквивалентно постановке следующих двух задач лексикографической
оптимизации:
![\begin{displaymath}P_p(r):\ \max\nolimits_p \left \{ \left [
\begin{array}{c}
...
...\\ (c,\ x)
\end{array} \right ] \ \vert \ x\in M(r) \right \},\end{displaymath}](img527.gif)
![\begin{displaymath}P_q^{\char93 }(R):\ \min\nolimits_q \left \{ \left [
\begin{...
... \end{array} \right ] \ \vert \ u\in M^{\char93 }(R) \right \},\end{displaymath}](img528.gif)
Теорема 4.1. Пусть нормы
![]() монотонны
вместе со своими сопряженными и кусочно-линейны. Тогда
существует не пустая область конструктивно определяемых
монотонны
вместе со своими сопряженными и кусочно-линейны. Тогда
существует не пустая область конструктивно определяемых
![]() и
и ![]() таких, что
таких, что
| (4.1) |
| (4.2) |
| (4.3) |
П о я с н е н и я к д о к а з а т
е л ь с т в у. Соотношение (4.3) выполняется в силу основной теоремы
двойственности для несобственных задач ЛП (она была приведена в
п. 1). Что касается соотношений (4.1) и (4.2), то суть их
доказательств та же, что и теоремы (2.1). Уточнения требует лишь
следующее обстоятельство. Когда мы определяем
![]() , где
, где
![]() двойственная
оценка ограничения
двойственная
оценка ограничения
![]()
![]() в задаче
в задаче
| (4.4) |
Рассмотрим частный случай задач Pp(r) и Pq#(R) в форме:
| (4.5) |
Нас будет интересовать случай несобственности L 3-го рода:
Задачи P и P# из п. 1.3, соответствующие рассматриваемой
ситуации, запишем в следующей форме:
| (4.6) |
| (4.7) |
Отмеченный эффект различия в рассматриваемом случае исчезает,
что объясняется условием
![]() ,
, ![]() . Ниже будет показано,
что при некоторых предположениях (уже фигурировавших ранее)
реализуется следующая схема двойственности:
. Ниже будет показано,
что при некоторых предположениях (уже фигурировавших ранее)
реализуется следующая схема двойственности:
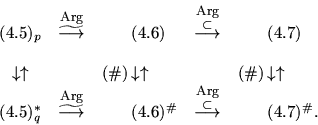
Здесь
![]() означает
означает
![]() .
Обратим внимание на то, что в силу теоремы двойственности для НЗ
ЛП (см. п.1.3): opt(4.6)=opt(4.6)#.
.
Обратим внимание на то, что в силу теоремы двойственности для НЗ
ЛП (см. п.1.3): opt(4.6)=opt(4.6)#.
Теорема 4.2. Пусть нормы
![]() и
и
![]() монотонны (вместе со своими
сопряженными) и кусочно-линейны. Тогда существует не пустая
область конструктивно определяемых r>0 и R>0 таких, что
реализуется выше приведенная схема.
монотонны (вместе со своими
сопряженными) и кусочно-линейны. Тогда существует не пустая
область конструктивно определяемых r>0 и R>0 таких, что
реализуется выше приведенная схема.
Д о к а з а т е л ь с т в о.
Справедливость левой части схемы определяется теоремой 4.1.
Убедимся в справедливости правой части нашей схемы, т.е. в
справедливости включений Arg(4.6)![]() Arg(4.7) и
Arg
Arg(4.7) и
Arg
![]() Arg(4.7)#.
Рассмотрим, например, первое из них. Максимизируемые
функции в (4.6) и (4.7) обозначим через f1(x) и f2(x),
соответственно. Эти функции являются вогнутыми. В силу
смысла числа
Arg(4.7)#.
Рассмотрим, например, первое из них. Максимизируемые
функции в (4.6) и (4.7) обозначим через f1(x) и f2(x),
соответственно. Эти функции являются вогнутыми. В силу
смысла числа
![]() имеем
имеем
![]() для любых
допустимых x, т.е. для
для любых
допустимых x, т.е. для ![]() ,
,
![]() .
При этом, если
.
При этом, если ![]() Arg(4.6), то с
использованием верхнего соотношения левой части схемы получим
Arg(4.6), то с
использованием верхнего соотношения левой части схемы получим
![]() , следовательно,
opt
, следовательно,
opt
![]() , отсюда вытекает
, отсюда вытекает ![]() Arg(4.7),
т.е. доказываемое включение справедливо. Аналогично
доказывается и второе включение, надо лишь учесть тот факт,
что если норма кусочно-линейна, то и сопряженная норма
является таковой.
Arg(4.7),
т.е. доказываемое включение справедливо. Аналогично
доказывается и второе включение, надо лишь учесть тот факт,
что если норма кусочно-линейна, то и сопряженная норма
является таковой.
Будем отталкиваться от l-постановки задачи
квадратичного программирования следующего вида:
Задаче
![]() поставим в соответствие
l-задачу
поставим в соответствие
l-задачу
Теорема 5.1. При условии совместности
при любых ![]() системы
системы ![]() существует не пустая
область значений векторных параметров r и R таких, что
существует не пустая
область значений векторных параметров r и R таких, что
З а м е ч а н и е. Теоремы такого типа, сформулированные выше, имеют однотипное доказательство. Это наводит на мысль, что возможна такая общая постановка задачи и формулировка общей теоремы двойственности, из которой указанные теоремы вытекали бы в качестве следствий. В значительной степени это так и есть. Однако, во-первых, как задача, так и формулировка были бы при этом громоздкими, а во-вторых, были бы утеряны естественные по своей постановке формы задания исходной задачи. Впрочем, надо все же отметить, что у доказательства названных теорем есть свои нюансы.
Каснемся еще одной ситуации, относящейся к несобственной
задаче квадратичного программирования
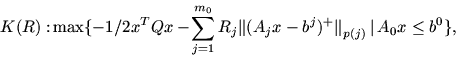
![\begin{displaymath}K_l:\ \max\nolimits_p \left \{ \left [
\begin{array}{l}-1/2x...
...{m_0}(x) \end{array} \right ] \ \vert \ A_0x\leq b^0 \right \},\end{displaymath}](img586.gif)
Теорема 5.2. Пусть выполнены условия:
![]() положительно определенная матрица;
положительно определенная матрица;
20. подсистема ![]() системы
системы ![]() совместна;
совместна;
30. нормы
![]() кусочно-линейны
и монотонны.
кусочно-линейны
и монотонны.
Тогда существует не пустая область значений Rj
(j=1,..., m0) таких, что
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ
90С25
Eremin, I.I.
The lexicographic duality for improper problems in
linear and quadratic programming. (Russian)
Trudy Inst. Mat. i Mekh. (Ekaterinburg) 1 (1992), 178-192.
This paper deals with lexicographic duality in linear and quadratic programming. The problem is so considered as how to formulate the primary lexicographic program to obtain the dual program which would permit lexicographic interpretation. Moreover, these programs must be connected by substantial mathematical relationships. In the paper this problem is solved for linear and quadratic programs.