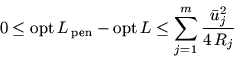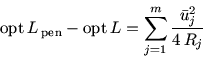

Next: II Лексикографическая двойственность для
Up: book
Previous: book
Двойственность в математическом
программировании (МП), как и вообще в математике, играет
фундаментальную роль. Она выступает в качестве краеугольного камня
соответствующих теорий, порождает арсенал конструктивных средств
анализа математических моделей, построения эффективных алгоритмов
решения задач и формальной оценки этой эффективности.
Если  - некоторый исходный математический объект
(модель), то двойственный объект
- некоторый исходный математический объект
(модель), то двойственный объект
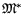 , вообще говоря,
выступает как некий внешний по отношению к
, вообще говоря,
выступает как некий внешний по отношению к 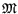 объект ''наблюдения'' за
объект ''наблюдения'' за 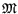 . Конечно, двойственность в
зависимости от ее конкретного содержания, определяемого конкретной
математической дисциплиной (алгебра, функциональный анализ, выпуклый
анализ, теория оптимального управления и т.д.), несет в себе следы
специфики соответствующей дисциплины. Но именно это обстоятельство и
превращает двойственность в математике в здание хотя в определенном
смысле и единой, но гармонически организованной и насыщенной
архитектуры.
. Конечно, двойственность в
зависимости от ее конкретного содержания, определяемого конкретной
математической дисциплиной (алгебра, функциональный анализ, выпуклый
анализ, теория оптимального управления и т.д.), несет в себе следы
специфики соответствующей дисциплины. Но именно это обстоятельство и
превращает двойственность в математике в здание хотя в определенном
смысле и единой, но гармонически организованной и насыщенной
архитектуры.
Содержание двойственности в математическом
программировании состоит в сопоставлении исходной задаче C
другой задачи 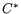 , формируемой по определенным правилам и
называемой двойственной. Эти задачи связаны математически
содержательными соотношениями, позволяющими, например, получить
оценки критериальной эффективности всех параметров, формирующих
задачу C; свести решение оптимизационной задачи к решению некоторой
системы неравенств; сформировать в изящной форме условия
оптимальности; оценить скорость сходимости итерационных процессов для
задачи C и т.д.
, формируемой по определенным правилам и
называемой двойственной. Эти задачи связаны математически
содержательными соотношениями, позволяющими, например, получить
оценки критериальной эффективности всех параметров, формирующих
задачу C; свести решение оптимизационной задачи к решению некоторой
системы неравенств; сформировать в изящной форме условия
оптимальности; оценить скорость сходимости итерационных процессов для
задачи C и т.д.
Если задача МП (или ЛП) - результат моделирования конкретной
экономической (производственной) ситуации, то двойственность и та
информация, которую двойственность порождает, позволяют провести
глубокий анализ моделируемой ситуации (моделируемого объекта),
выявить узкие места, тенденции динамики объекта, выразив эти факторы
в количественной форме. За такого рода анализом закрепился термин -
экономико-математический анализ. Профессионально сделанные
пакеты прикладных программ (ППП), решающие задачи МП или ЛП, обычно
выдают в форме удобных распечаток всю совокупность информации,
необходимую для экономико-математического анализа. Это дает
экономистам хорошие возможности для оценки состояния экономических
(или производственных) систем и идентификации параметров управления.
Ниже конспективно излагается материал по двойственности для
различных классов задач МП (преимущественно линейных), а именно:
стандартных задач ЛП, несобственных, лексикографических,
паретовских, дизъюнктивных и др.
1. Задача линейного программирования и ее
экономическая интерпретация
Выпишем задачу ЛП в удобном для дальнейшего виде:
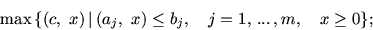 |
(1.1) |
здесь
![$c=[c_1,\,...\,,c_n]^T$](img13.gif) ,
,
![$a_j=[a_{j1},\,...\,,a_{jn}]^T$](img14.gif) . Введя обозначения
. Введя обозначения
![$b=[b_1,\,...\,,b_m]^T$](img15.gif) ,
,
![$A=[a_{ji}]_{1,1}^{m,n}$](img16.gif) ,
,
![$X=[x_1,\,...\,,x_n]^T$](img17.gif) , задачу (1.1) можно переписать в
матричном виде
, задачу (1.1) можно переписать в
матричном виде
Дадим экономическую интерпретацию этой задачи.
Пусть имеется некое производство, выступающее в качестве
преобразователя
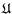 системы исходных ингредиентов
системы исходных ингредиентов
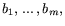 обладающих ценностью, в новую систему
носителей ценности - совокупность продуктов. Термины
производство, ценность, продукт, а ниже - оценка (как
измеритель ценности) будут употребляться в качестве исходных.
обладающих ценностью, в новую систему
носителей ценности - совокупность продуктов. Термины
производство, ценность, продукт, а ниже - оценка (как
измеритель ценности) будут употребляться в качестве исходных.
Преобразуемыми ингредиентами могут быть: основные фонды и
оборотные средства (оборудование, производственные площади, виды
транспорта, сырье, электроэнергия и т.д.), природные ресурсы
(полезные ископаемые, земля, воды рек и озер и др.), трудовые
ресурсы, классифицированные по специальностям и уровню квалификации.
В основу преобразования ингредиентов положим некоторую конечную
совокупность технологических способов, моделируемых векторами
при этом координаты вектора pi будем интерпретировать как
затраты ингредиентов, приходящиеся на единичную интенсивность (например на единицу времени) использования i-го
технологического способа. Саму же интенсивность обозначим
через xi (xi =1 - единичная интенсивность).
Предположим, что затраты ингредиентов и создаваемая ценность
подчиняются закону линейной зависимости от вектора интенсивностей
![$x=[\, x_1,\,...\,,x_n \,]^T$](img22.gif) . В этом
предположении затраты j-го ингредиента, отнесенные к вектору x,
выразятся величиной
. В этом
предположении затраты j-го ингредиента, отнесенные к вектору x,
выразятся величиной 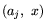 ,
, 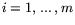 . Так как границы
сверху для них определены числами bj, то должны выполняться
неравенства
. Так как границы
сверху для них определены числами bj, то должны выполняться
неравенства
Содержательный смысл вектора x, задающего уровень
производства, диктует ограничение 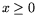 . Таким образом, нами
получена система ограничений задачи (1.1). Сказанное может быть
подытожено схемой
. Таким образом, нами
получена система ограничений задачи (1.1). Сказанное может быть
подытожено схемой
при этом
![$x\geq 0,\ \ y\leq b = [\, b_1,\,...\,,b_m \,]^T$](img28.gif) .
.
Если ci понимать как оценку ценности, заключенной в
носителе конечного результата применения i-го технологического
способа с интенсивностью xi=1, то величина
будет выражать суммарную оценку ценности, заключенной в конечных
носителях результата преобразования исходных ингредиентов в
соответствии с уровнем производства, задаваемым вектором x.
Следовательно, задача (1.1) решает вопрос об отыскании уровня производства (вектора интенсивностей), подчиненного
условиям технологической допустимости (формально - системе линейных
неравенств) и доставляющего для 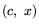 максимальное значение.
максимальное значение.
Возможна несколько модифицированная интерпретация
задачи (1.1), а именно: пусть xi - объем производства
продукции i-го вида по i-му технологическому способу, ci -
цена реализации единицы продукции i-го вида. Тогда 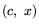 выражает доход от реализации продукции, который максимизируется.
выражает доход от реализации продукции, который максимизируется.
Остановимся на полезной интерпретации задачи ЛП в форме
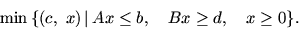 |
(1.2) |
В основу положим перечень технологических способов 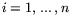 с
интенсивностями
с
интенсивностями 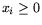 их использования; ci -
трудозатраты на единицу интенсивности xi=1; b - вектор
ресурсов; i-ый столбец pi матрицы A - вектор затрат
ресурсов, приходящихся на единичную интенсивность xi=1; i-ый
столбец hi матрицы B - вектор выпуска продукции, приходящийся
на единичную интенсивность xi=1; d - зафиксированный уровень
производства продукции. Модель (1.2) в введенных терминах
читается так: отыскать уровень производства
их использования; ci -
трудозатраты на единицу интенсивности xi=1; b - вектор
ресурсов; i-ый столбец pi матрицы A - вектор затрат
ресурсов, приходящихся на единичную интенсивность xi=1; i-ый
столбец hi матрицы B - вектор выпуска продукции, приходящийся
на единичную интенсивность xi=1; d - зафиксированный уровень
производства продукции. Модель (1.2) в введенных терминах
читается так: отыскать уровень производства 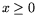 ,
удовлетворяющий ресурсным ограничениям
,
удовлетворяющий ресурсным ограничениям 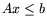 и условиям на
необходимый уровень производства продукции
и условиям на
необходимый уровень производства продукции 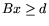 , обеспечивающий
минимум трудозатрат.
, обеспечивающий
минимум трудозатрат.
По существу, модель (1.2) и приведенная
интерпретация (с возможностями расширения объема содержания
введенных терминов) реализуют синтез требований и характеристик
общеэкономического уровня, предъявляемых ко всякой естественной экономике. Положив M=
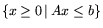 ,
,
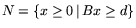 , ситуацию модели (1.2)
можно изобразить геометрически: см. Рис. 1.
, ситуацию модели (1.2)
можно изобразить геометрически: см. Рис. 1.
На рисунке
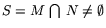 ,
, 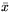 - вектор оптимального уровня производства, отвечающий направлению
изображенного вектора c. Многогранники M и N выступают в
качестве областей ''ресурсных возможностей'' и ''потребностей''.
На практике, да и в общем смысле (в соответствии с аксиомами
''общества потребления''), многогранники M и N находятся в
состоянии ''противостояния'', несогласованности, что можно выразить
пустотой их пересечения:
- вектор оптимального уровня производства, отвечающий направлению
изображенного вектора c. Многогранники M и N выступают в
качестве областей ''ресурсных возможностей'' и ''потребностей''.
На практике, да и в общем смысле (в соответствии с аксиомами
''общества потребления''), многогранники M и N находятся в
состоянии ''противостояния'', несогласованности, что можно выразить
пустотой их пересечения:
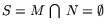 .
.
Обобщением модели (1.2) в смысле задания структуры ее
ограничений могла бы служить система неравенств
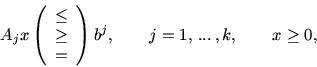 |
(1.3) |
где Ajx и bj соединены одним из перечисленных
отношений порядка. Это соответствует возможности как угодно полной
структуризации всех участвующих в экономическом (производственном)
процессе факторов, покрывающих области ресурсных, технологических и
потребительских описаний. Детализация моделей типа (1.2) при
ограничениях (1.3) приводит к различным классическим моделям
математической экономики. В (1.3) отдельные блоки (т.е.
подсистемы при различных j) могут не согласовываться (вступать в
противоречие), т.е. при объединении давать несовместные системы.
Такие ситуации соответствуют так называемым несобственным
задачам линейного программирования.
2. Игра двух лиц с нулевой
суммой
Игра двух лиц определяется: 1) перечнем игроков (1-ый игрок, 2-ой игрок), 2) множествами X и
U стратегий x и u 1-го и 2-го игроков
соответственно и 3) платежными функциями 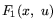 и
и
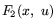 , означающими выигрыши игроков при независимом выборе ими
стратегий
, означающими выигрыши игроков при независимом выборе ими
стратегий 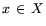 и
и 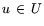 . Если
. Если
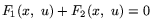 , т.е. выигрыш 1-го игрока равен проигрышу 2-го, то игра
называется игрой с нулевой суммой. В случае такой игры можно
оперировать лишь функцией выигрыша 1-го игрока
, т.е. выигрыш 1-го игрока равен проигрышу 2-го, то игра
называется игрой с нулевой суммой. В случае такой игры можно
оперировать лишь функцией выигрыша 1-го игрока
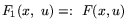 , она же - функция проигрыша для 2-го игрока. Одним из
важнейших принципов анализа такой игры является принцип гарантированного результата. Он направлен на отыскание игроками
стратегий, обеспечивающих гарантированные выигрыши. Формализацию
такого подхода можно осуществить путем следующих рассуждений. Если
1-ый игрок зафиксирует свою стратегию
, она же - функция проигрыша для 2-го игрока. Одним из
важнейших принципов анализа такой игры является принцип гарантированного результата. Он направлен на отыскание игроками
стратегий, обеспечивающих гарантированные выигрыши. Формализацию
такого подхода можно осуществить путем следующих рассуждений. Если
1-ый игрок зафиксирует свою стратегию 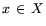 , то он может
подсчитать свой гарантированный выигрыш
, то он может
подсчитать свой гарантированный выигрыш
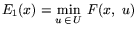 , а затем его максимизировать,
т.е. подсчитать
, а затем его максимизировать,
т.е. подсчитать
Для 2-го игрока такой подход дает
Таким образом, содержательно возникли две задачи:
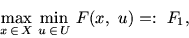 |
(2.1) |
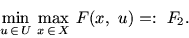 |
(2.2) |
Если
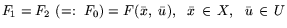 , то число F0 называется ценой игры, а
, то число F0 называется ценой игры, а
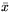 и
и 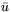 - оптимальными стратегиями 1-го
и 2-го игроков соответственно (стратегиями равновесия). Вообще
говоря, совпадение F1 и F2 необязательно.
Задачи (2.1) и (2.2) по совокупности будем называть
формализацией игры двух лиц с нулевой суммой на основе
принципа гарантированного результата.
- оптимальными стратегиями 1-го
и 2-го игроков соответственно (стратегиями равновесия). Вообще
говоря, совпадение F1 и F2 необязательно.
Задачи (2.1) и (2.2) по совокупности будем называть
формализацией игры двух лиц с нулевой суммой на основе
принципа гарантированного результата.
3. Игровая модель ''Производство - Рынок''
На задачу L можно смотреть как на модель Производства (учитывая данную ей экономическую интерпретацию).
Осуществим расширение ситуации за счет включения Рынка,
образуя таким образом систему ''Производство-Рынок'':
Рассмотрим Производство в роли 1-го игрока с множеством
стратегий
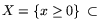 En, а Рынок - в
роли 2-го игрока с функциями: 1) поглощение продукции Производства по фиксированным ценам ci,
En, а Рынок - в
роли 2-го игрока с функциями: 1) поглощение продукции Производства по фиксированным ценам ci, 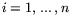 и
2) поглощение (покупка) или продажа ресурсов по ценам игрового
взаимодействия в системе ''Производство - Рынок''. Множеством
стратегий ''Рынка'' будет совокупность ценовых векторов
и
2) поглощение (покупка) или продажа ресурсов по ценам игрового
взаимодействия в системе ''Производство - Рынок''. Множеством
стратегий ''Рынка'' будет совокупность ценовых векторов
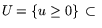 Em, т.е. uj - цена единицы ресурса с
номером j,
Em, т.е. uj - цена единицы ресурса с
номером j, 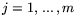 . В роли платежной функции в данной игре
выступает
. В роли платежной функции в данной игре
выступает
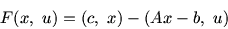 |
(3.1) |
являющаяся функцией Лагранжа, соотнесенной задаче L. Эта
функция, очевидно, и имеет смысл выигрыша (дохода) 1-го игрока в
результате реализации игроками своих стратегий 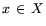 и
и 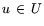 , т.е. в результате обменных операций по продукции и ресурсам:
, т.е. в результате обменных операций по продукции и ресурсам:
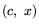 - доход от продажи продукции xi по фиксированным
ценам ci,
- доход от продажи продукции xi по фиксированным
ценам ci, 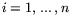 ; если
; если
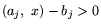 , то
, то
![$u_j\,[(a_j,\ x) -b_j]$](img63.gif) - плата 1-го игрока 2-му игроку за покупку
j-го ресурса в количестве
- плата 1-го игрока 2-му игроку за покупку
j-го ресурса в количестве
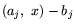 по цене uj; если
по цене uj; если
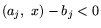 , то слагаемое
, то слагаемое
![$-u_j\,[(a_j,\ x) -b_j] = u_j\,[b_j
-(a_j,\ x)]$](img66.gif) читается как доход 1-го игрока от продажи излишков j-го
ресурса в количестве
читается как доход 1-го игрока от продажи излишков j-го
ресурса в количестве
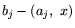 по цене uj,
по цене uj, 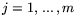 .
Следовательно, вся сумма
.
Следовательно, вся сумма
![$-\mbox{$\sum\limits_{j=1}^{m}$} u_j\, [(a_j,\ x) -b_j]
=-(Ax-b,\ u)$](img68.gif) - это доход 1-го игрока от совокупности рыночных
операций по продаже излишков и покупке недостающих ресурсов,
рассчитанных на уровень производства x, а
- это доход 1-го игрока от совокупности рыночных
операций по продаже излишков и покупке недостающих ресурсов,
рассчитанных на уровень производства x, а 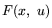 - доход 1-го
игрока в целом.
- доход 1-го
игрока в целом.
Принцип гарантированного результата, примененный к
сформулированной игре, приводит к задачам:
![\begin{displaymath}
\max_{x\geq 0}\, \min_{u\geq 0}\,[(c,\ x) -(Ax-b,\ u)],
\end{displaymath}](img70.gif) |
(3.2) |
![\begin{displaymath}
\min_{u\geq 0}\, \max_{x\geq 0}\,[(c,\ x) -(Ax-b,\ u)].
\end{displaymath}](img71.gif) |
(3.3) |
К ним применимы все определения, сформулированные для задач
(2.1) и (2.2). В данной ситуации оптимальную
стратегию 1-го игрока (Производства) естественно назвать
оптимальным планом, а оптимальную стратегию 2-го игрока (Рынка) - вектором оптимальных (равновесных)
цен на ресурсы. На самом деле, понятия оптимального плана в
смысле оптимальной стратегии и оптимального плана задачи L
совпадают.
4. Игровой подход к
двойственности
Содержательный подход к двойственности, т.е. подход к
формулировке задачи 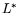 - двойственной к L, может быть
реализован путем установления следующих эквивалентных переходов
- двойственной к L, может быть
реализован путем установления следующих эквивалентных переходов
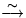 :
:
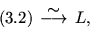 |
(4.1) |
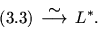 |
(4.2) |
Здесь эквивалентный переход означает эквивалентное
преобразование. Обратимся к (4.1). Рассмотрим внутреннюю
операцию в (3.2), т.е.
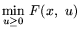 .
.
(здесь 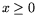 ). Отсюда и следует
). Отсюда и следует
т.е. имеет место (4.1). Убедимся в
справедливости (4.2). Преобразуем вначале функцию Лагранжа
|
F(x, u) =(c, x) -(Ax-b, u) = (b, u) +(-ATu+c, x).
|
(4.3) |
Рассмотрим внутреннюю операцию в (3.3), т.е.
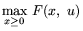 . Имеем
. Имеем
(здесь 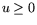 ). Отсюда и следует
). Отсюда и следует
Итак, задачу 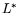 - двойственную к L, мы получили как
эквивалент игровой задачи (3.3) в рамках игровой модели
''Производство - Рынок'', при этом (3.3), а следовательно
и
- двойственную к L, мы получили как
эквивалент игровой задачи (3.3) в рамках игровой модели
''Производство - Рынок'', при этом (3.3), а следовательно
и 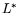 , выступает как задача построения оптимальных
(равновесных) цен на ресурсы. Вместе с тем мы получили
эквивалентность задачи L игровой задаче (3.2). Это, в
частности, дает оптимальность
, выступает как задача построения оптимальных
(равновесных) цен на ресурсы. Вместе с тем мы получили
эквивалентность задачи L игровой задаче (3.2). Это, в
частности, дает оптимальность 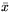 для L, если
для L, если 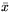 -
оптимальная стратегия игры (3.2), (3.3); и обратно: если
-
оптимальная стратегия игры (3.2), (3.3); и обратно: если
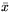 - оптимальное решение (оптимальный план) задачи L, то
при некотором
- оптимальное решение (оптимальный план) задачи L, то
при некотором
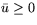 пара
пара
![$[\bar{x},\ \bar{u}]$](img86.gif) будет
отвечать определению оптимальных стратегий игроков.
будет
отвечать определению оптимальных стратегий игроков.
5. Подход к двойственности, связанный с
переобозначением роли переменных x и u
в функции Лагранжа
Функция Лагранжа исторически возникла в исследованиях
аналитических механиков (Лагранж, Фурье, Фаркаш, Остроградский и
др.) по проблеме равновесия механических систем при связях в форме
уравнений и неравенств. Равновесие в механических системах сопряжено
с состоянием, соответствующим минимуму потенциальной энергии.
Функция Лагранжа может быть соотнесена вообще любой задаче на
условный экстремум, при этом необходимо соблюсти вполне определенное
правило такого соотнесения. Выпишем эти правила (прямое и обратное)
для задач на 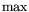 и
и 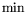 в двух формах:
в двух формах:
Обратное соответствие
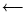 неоднозначно в связи с
возможностью переписать
неоднозначно в связи с
возможностью переписать 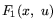 и
и 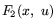 в
виде
в
виде
![$F_1(x,\ u) =f(x) +\mbox{$\sum\limits_{j=1}^{m}$} u_j\, [-f_j(x)]$](img94.gif) ,
,
![$F_2(x,
u) =f(x) -\mbox{$\sum\limits_{j=1}^{m}$} u_j\, [-f_j(x)]$](img95.gif) . Тогда справедливы и такие
соответствия:
. Тогда справедливы и такие
соответствия:
и
Схема рассмотренных соответствий не противоречит логике
механического смысла функции Лагранжа. Эту схему изобразим в кратком
виде:
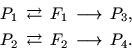 |
(5.1) |
Применим ее к задаче L и ее функции Лагранжа.
Равенство (4.3) позволяет посмотреть на функцию Лагранжа F(x,
u) иначе, а именно: на u как на переменную, а на x как на
вектор множителей Лагранжа. Тогда по правилу соответствия
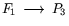 будем иметь:
будем иметь:
т.е. задача 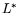 возникла как результат
реализации соответствия
возникла как результат
реализации соответствия
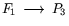 , в котором в
выражении функции Лагранжа переменные x и u поменялись
своими смысловыми ролями. Приведем более полную картину применения
схемы (5.1):
, в котором в
выражении функции Лагранжа переменные x и u поменялись
своими смысловыми ролями. Приведем более полную картину применения
схемы (5.1):
Заметим, что правило перехода  к двойственной задаче в
верхней строчке схемы согласуется с правилом перехода
к двойственной задаче в
верхней строчке схемы согласуется с правилом перехода  в
нижней строчке.
в
нижней строчке.
6. Построение двойственной задачи на основе
термодинамической аксиоматики
Оттолкнемся от схемы:
![\begin{picture}(120,30)(0,0)
\put (35,15){\framebox (50,10)[c]{Производство}}
...
...105,16){\makebox(0,0)[c]{$x$}}
\put (128,20){\makebox(0,0)[c]{,}}
\end{picture}](img103.gif)
в которой изображен Преобразователь (под термином
Производство) входа (вектор ресурсов b) в выход (вектор
продукции x). В принятой интерпретации задачи ЛП (1.1)
вектор исходных ингредиентов (ресурсов) b не наделен системой цен - как измерителей ценностей этих ингредиентов, вектор
же продукции такими измерителями наделен - это вектор c. Можно на
систему ценностных измерителей посмотреть более широко, а именно -
как на систему неких энергетических измерителей,
подчиняющихся законам термодинамики, запрещающих для любого
энергетического преобразователя КПД (коэффициент полезного действия)
больше единицы. В нашей ситуации это означает, что суммарная энергетическая оценка входа должна быть не меньше, чем аналогичная
оценка выхода. Если вектор c трактовать как вектор энергетических измерителей продукции x, а 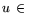 En+ - подлежащий определению вектор энергетических
измерителей исходных ингредиентов, то высказанная аксиома может быть
выражена неравенством
En+ - подлежащий определению вектор энергетических
измерителей исходных ингредиентов, то высказанная аксиома может быть
выражена неравенством
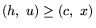 . В частности, если
h=hi - i-ый столбец матрицы A, выражающий расход
ингредиентов на единицу продукции i-го вида и оцениваемый
величиной ci, то выписанное неравенство примет вид
. В частности, если
h=hi - i-ый столбец матрицы A, выражающий расход
ингредиентов на единицу продукции i-го вида и оцениваемый
величиной ci, то выписанное неравенство примет вид
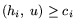 .
.
Свойства, накладываемые на Преобразователь, сформулируем в форме
следующих аксиом:
- 1)
- суммарная оценка используемых ингредиентов подчиняется закону
линейной зависимости от вектора их оценок uj,
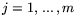 ;
;
- 2)
- суммарная оценка ингредиентов, расходуемых в результате
применения i-го технологического способа на единицу
продукции, не менее оценки ci получаемой единицы этой
продукции;
- 3)
- оптимальные оценки ингредиентов определяются из условия
максимума КПД Преобразователя.
Условия 1) и 2) диктуют систему линейных ограничений
с многогранником 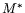 . Условие 3) формулирует задачу
. Условие 3) формулирует задачу
при этом, естественно,
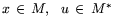 . В
соответствии с этим
. В
соответствии с этим
В числителе данного соотношения стоит задача L, моделирующая
Производство, в знаменателе - задача 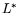 - двойственная
к L, моделирующая задачу отыскания оптимальных оценок (в энергетическом истолковании) исходных ингредиентов.
- двойственная
к L, моделирующая задачу отыскания оптимальных оценок (в энергетическом истолковании) исходных ингредиентов.
В изложенной интерпретации задачи 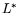 употребленный термин
''энергетическая оценка'' имеет чисто ассоциативный смысл, и
большего в него вкладывать не следует (по крайней мере в рамках
данного кратко изложенного подхода к формированию двойственности
в ЛП).
употребленный термин
''энергетическая оценка'' имеет чисто ассоциативный смысл, и
большего в него вкладывать не следует (по крайней мере в рамках
данного кратко изложенного подхода к формированию двойственности
в ЛП).
7. Теорема двойственности
Сформулируем основные утверждения, связывающие задачи
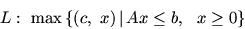 |
(7.1) |
и
Введем стандартные обозначения:
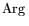 L - оптимальное
множество задачи L,
L - оптимальное
множество задачи L,
 L - конкретный элемент из
L - конкретный элемент из
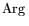 L,
L,
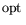 L - оптимальное значение задачи L. Если S - символ
для обозначения некоторой системы линейных неравенств, то
L - оптимальное значение задачи L. Если S - символ
для обозначения некоторой системы линейных неравенств, то
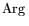 S
будет означать множество ее решений. Отметим очевидные соотношения:
S
будет означать множество ее решений. Отметим очевидные соотношения:
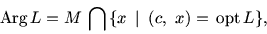
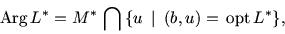
где
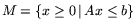 ,
,
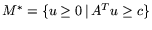 .
.
Теорема 7.1
Справедливо неравенство
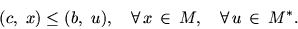
Следствие 7.1
Если
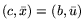
,
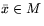
,
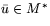
, то
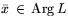
,
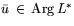
.
Теорема 7.2 (двойственности)
Если задача
L разрешима, то
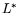
также разрешима, при
этом их оптимальные значения совпадают.
Теорема 7.3
Двойственная задача к двойственной совпадает с исходной, т.е.
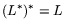
.
З а м е ч а н и е 7.1. Свойство взаимности
является универсальным, т.е. не зависит от формы задания исходной
задачи.
З а м е ч а н и е 7.2. Теорема 7.2 в силу
свойства взаимности допускает и такую редакцию: из
разрешимости 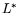 вытекает разрешимость L и совпадение их
оптимальных значений.
вытекает разрешимость L и совпадение их
оптимальных значений.
Теорема 7.2 позволяет сформулировать следующее утверждение.
Теорема 7.4
Задача
L разрешима тогда и только тогда, когда
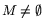
,
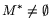
.
Задачам (7.1) и (7.1) поставим в
соответствие систему линейных неравенств
поставим в
соответствие систему линейных неравенств
![\begin{displaymath}
\left. \begin{array}{crcr}
S: & Ax\leq b, & & A^Tu\geq c,\...
...[8pt]
& (c,\ x) & \quad\geq & (b,\ u).
\end{array}\right \}
\end{displaymath}](img131.gif) |
(7.2) |
Задача нахождения хотя бы одного решения этой системы
называется
симметрической задачей.
Связь между задачами L, 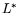 в форме (7.1),
(7.1)
в форме (7.1),
(7.1) и системой S устанавливает
и системой S устанавливает
Теорема 7.5
Задача
L и система
S одновременно разрешимы или неразрешимы,
при этом в случае разрешимости
т.е. множество решений системы
S является декартовым
произведением оптимальных множеств задач
L и
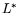
.
Приведем схему формирования двойственной задачи 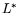 при
задании L в самом общем виде.
при
задании L в самом общем виде.
Сказанное выше о взаимных свойствах пары двойственных задач ЛП
сохраняется, естественно, и для выписанной пары задач
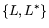
.
В заключение данного пункта остановимся на некоторых
содержательных аспектах двойственности. При игровом подходе к
двойственности, т.е. к формированию двойственной задачи 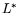 (см. п. 4), переменный вектор
(см. п. 4), переменный вектор 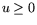 выступает как вектор
допустимых цен на ресурсы в игре ''Производство-Рынок'', а
оптимальный вектор цен
выступает как вектор
допустимых цен на ресурсы в игре ''Производство-Рынок'', а
оптимальный вектор цен
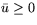 в силу
эквивалентности (4.2) как оптимальный вектор задачи
в силу
эквивалентности (4.2) как оптимальный вектор задачи 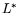 .
Таким образом, задача L как модель производства с фиксированными
ценами на продукт дополняется моделью определения оптимальных цен
(двойственных оценок) на ресурсы.
.
Таким образом, задача L как модель производства с фиксированными
ценами на продукт дополняется моделью определения оптимальных цен
(двойственных оценок) на ресурсы.
В соответствии с подходом к двойственности, изложенным в
п. 6,
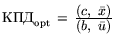 , где
, где
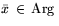 L,
L,
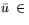
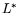 . По теореме двойственности
. По теореме двойственности
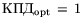 (
(
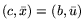 ), т.е. при оптимальном плане
), т.е. при оптимальном плане  Производства и
оптимальных ценах
Производства и
оптимальных ценах  на ресурсы схема, изображенная на
стр.
на ресурсы схема, изображенная на
стр. ![[*]](crossref.gif) ,
работает с коэффициентом полезного действия,
равным единице. Заметим, что расширительного толкования этому
факту придавать не следует.
,
работает с коэффициентом полезного действия,
равным единице. Заметим, что расширительного толкования этому
факту придавать не следует.
8. Элементы маргинального анализа
Двойственность для задач ЛП позволяет исследовать некоторые
дифференциальные свойства функции оптимума
 optL, где L -- произвольная задача ЛП,
optL, где L -- произвольная задача ЛП,
![$y=[A,\ b,\ c \,]$](img140.gif) .
.
Пусть
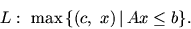 |
(8.1) |
Теорема о маргинальных значениях для L - это теорема о
формульном представлении производной функции оптимума 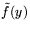 по произвольному направлению l из пространства вектора y.
Примем в качестве l вектор
по произвольному направлению l из пространства вектора y.
Примем в качестве l вектор
![$[\bigtriangleup A,\ \bigtriangleup b,\ \bigtriangleup c \,]$](img143.gif) .
Частный случай этой ситуации реализуется соотношением
.
Частный случай этой ситуации реализуется соотношением
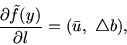 |
(8.2) |
в котором роль направления l играет вектор
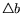 в
пространстве вектора b (как информационного параметра задачи L),
т.е.
в
пространстве вектора b (как информационного параметра задачи L),
т.е.
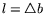 . Если оптимальный вектор
. Если оптимальный вектор 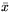 исходной
задачи (8.1) единственный, то имеет место аналог
соотношения (8.2) в форме
исходной
задачи (8.1) единственный, то имеет место аналог
соотношения (8.2) в форме
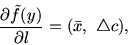 |
(8.3) |
где
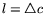 . В общем случае получение формулы для
. В общем случае получение формулы для
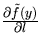 выводит за рамки
линейного анализа линейной задачи L.
выводит за рамки
линейного анализа линейной задачи L.
Теорема 8.1
Пусть выполнены для задачи
L условия:
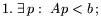
2. Оптимальные множества
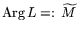
и
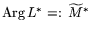
не пусты и ограничены.
Если
![$l= [\bigtriangleup A,\ \bigtriangleup b,\ \bigtriangleup c \,]$](img153.gif)
- произвольное
направление в пространстве вектора
![$y=[A,\ b,\ c \,]$](img140.gif)
, то
![\begin{displaymath}
\frac{\textstyle \partial \tilde {f}(y)}{\textstyle \partia...
...x}) -
(\bigtriangleup A\bar{x} -\bigtriangleup b,\ \bar{u})].
\end{displaymath}](img154.gif) |
(8.4) |
Следовательно, если
L и
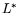
разрешимы в
единственных точках
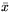
и
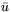
, то
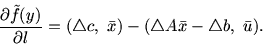 |
(8.5) |
Следствие 8.1
В предположениях, дающих (
8.5), справедливы соотношения:
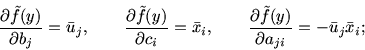 |
(8.6) |
здесь
![$\bar{u}^T =[\bar{u}_1,\,...\,,\bar{u}_m],\quad \bar{x}^T
= [\bar{x}_1,\,...\,,\bar{x}_n]$](img157.gif)
.
В обозначении функции оптимума 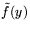 в качестве аргумента
ниже будем ставить тот фрагмент информационного вектора, который нас
интересует:
в качестве аргумента
ниже будем ставить тот фрагмент информационного вектора, который нас
интересует: 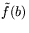 ,
,
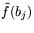 и т.д.
и т.д.
Сделаем замечание, связанное с содержательной интерпретацией
двойственных оценок 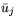 ,
, 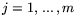 . В случае
единственности оптимального вектора
. В случае
единственности оптимального вектора 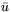 задачи
задачи 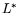 существует окрестность v(b) вектора
существует окрестность v(b) вектора
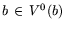 (V0
- внутренность множества V) такая, что
(V0
- внутренность множества V) такая, что
Тогда при некотором малом
t0>0 и
![$\forall \, t\,\in\,(0,
t_0 \,]$](img163.gif)
имеем
т.е.
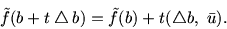 |
(8.7) |
Если
t0>1, т.е. в качестве
t, обеспечивающего
(
8.7), можно взять
t=1, то при
![$\bigtriangleup b =[0,\ldots ,\bigtriangleup
b_j=1,0,\ldots , 0]^T$](img166.gif)
из (
8.7) получается
Эти соотношения говорят о том, что оценки
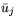
выступают в
качестве измерителей эффективности единицы
j-го ресурса
bj в
стандартной экономической интерпретации задачи
L.
9. Двойственность для несобственных задач
линейного программирования [23]
Под собственной задачей МП понимается разрешимая задача МП, для которой двойственная также разрешима и
оптимальные значения этих задач совпадают. В противном случае задача
называется несобственной (НЗ). В частности, если система
ограничений в задаче неразрешима (противоречивая), то задача -
несобственная. В случае задачи ЛП несобственность и неразрешимость
- понятия эквивалентные. Если
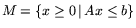 и
и
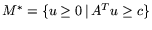 - допустимые
множества для пары взаимно двойственных задач ЛП, например, в
форме (1.1), то (как уже отмечалось) непустота M и
- допустимые
множества для пары взаимно двойственных задач ЛП, например, в
форме (1.1), то (как уже отмечалось) непустота M и
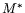 соответствует разрешимости этих задач. В случае
неразрешимости L (следовательно, и
соответствует разрешимости этих задач. В случае
неразрешимости L (следовательно, и 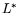 ) возможны три
альтернативы:
) возможны три
альтернативы:
- 1)
-
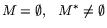 - НЗ ЛП 1-го рода,
- НЗ ЛП 1-го рода,
- 2)
-
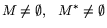 - НЗ ЛП 2-го рода,
- НЗ ЛП 2-го рода,
- 3)
-
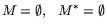 - НЗ ЛП 3-го рода.
- НЗ ЛП 3-го рода.
Причины и обстоятельства, порождающие неразрешимость модели,
разнообразны. Это, в частности: неадекватное моделирование,
противоречия между целями и ресурсными возможностями их достижения
(находящие свое отражение в модели), перегруженность требований к
объекту моделирования (например, к конструкции самолета),
некорректность постановки (в смысле некорректности по Тихонову),
противоречия между технологиями и средой (''грязные'' технологии и
требования экологии) и т.д.
При автоматизированном (программном) формировании модели трудно
разобраться в причинах несобственности, особенно тогда, когда этому
фактору нужно придать содержательную интерпретацию и дать
соответствующее объяснение. В случае задачи малой размерности, когда
она хорошо просматривается, ситуацию неразрешимости можно преодолеть
путем коррекции модели простыми средствами (проверить правильность
исходных данных, ослабить некоторые ограничения или совсем их
выбросит из модели и т.д.) и тем самым придти к разрешимой модели. В
случае модели высокой размерности (число ограничений и переменных -
тысячи и десятки тысяч) требуются более изощренные средства, причем
программно обеспеченные. Для реализации такого подхода уже требуются
теоретические наработки, в частности, теория двойственности,
являющаяся мощным генератором конструктивных средств всестороннего
анализа оптимизационных моделей. В основе двойственности для НЗ ЛП
лежит схема:
В ней
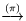 означает переход (сопоставление) задачам
L и L* по единому правилу
означает переход (сопоставление) задачам
L и L* по единому правилу 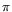 к разрешимым задачам
P и P*, обладающих свойствами:
(P#)# = P и
к разрешимым задачам
P и P*, обладающих свойствами:
(P#)# = P и
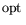 P =
P =
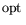 P#. Примерами реализаций Схемы 2 могут служить:
P#. Примерами реализаций Схемы 2 могут служить:
Здесь R и r - неотрицательные векторные параметры,
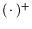 - положительная срезка вектора
- положительная срезка вектора 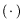 ,
R0 и r0 - неотрицательные числовые параметры,
,
R0 и r0 - неотрицательные числовые параметры,
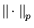 и
и
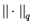 - произвольные нормы в соответствующих
пространствах,
- произвольные нормы в соответствующих
пространствах,
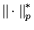 и
и
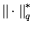 -
им сопряженные нормы.
-
им сопряженные нормы.
Приведем более общую реализацию приведенной схемы. Пусть
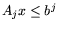
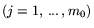 и
и
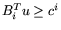
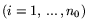 - произвольные разбиения систем
- произвольные разбиения систем 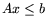 и
и
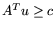 на
подсистемы (в предположении, что подсистемы
на
подсистемы (в предположении, что подсистемы 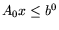 ,
, 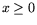 и
и
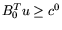 ,
, 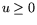 - совместны); {bj},
{uj}, {ci}, {xi} - разбиения векторов
- совместны); {bj},
{uj}, {ci}, {xi} - разбиения векторов 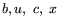 на подвекторы, соответствующие указанному разбиению. В
принятых обозначениях задачи P и P# могут быть записаны
следующим образом:
на подвекторы, соответствующие указанному разбиению. В
принятых обозначениях задачи P и P# могут быть записаны
следующим образом:
Теорема 9.1
1). Пусть
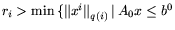
,
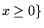
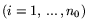
и задача
P разрешима. Тогда
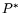
разрешима и
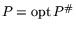
.
2). Если
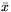
и
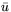
допустимы для
P и
P# соответственно, то
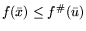
, где
f(
x)
и
f#(
u) - функции, оптимизируемые в
P и
P#. Отсюда
следует: если
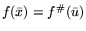
, то
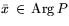
,
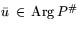
.
З а м е ч а н и е 9.1. Все нормы, фигурирующие в
написании задач P и P#, предполагаются монотонными.
З а м е ч а н и е 9.2. Справедлив и обратный
вариант теоремы.
З а м е ч а н и е 3. Решение задач P и P#
сводится к решению следующей системы линейных и выпуклых неравенств:
10. Двойственность для лексикографической
задачи
ЛП [42,47]
Двойственность в линейном программировании обладает двумя
замечательными свойствами:
- 10
- Если L - задача линейного программирования, то
двойственная задача
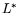 также задача
линейного программирования.
также задача
линейного программирования.
- 20
-
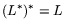 - свойство взаимности.
- свойство взаимности.
Нелинейное программирование (НП) уже вторым свойством не обладает
- за исключением квадратичного программирования. Первое же свойство
выполняется в таком банальном смысле: если исходная задача
нелинейная, то и двойственная задача также является нелинейной. Но
если взять определенный класс нелинейных задач, например, класс
задач выпуклого программирования (ВП), то переход к двойственности
выводит за этот класс (за редким исключением; таким исключением
является класс выпуклых квадратичных задач).
Ниже речь будет идти о задачах лексикографической оптимизации.
Возникает вопрос: как поставить задачу лексикографической
оптимизации, чтобы
- 1)
- формирование двойственной задачи давало также
лексикографическую задачу;
- 2)
- прямая и двойственная задачи были связаны естественными
математически содержательными соотношениями.
Один из реализованных подходов к его решению состоит в следующем.
Пусть
![\begin{displaymath}
\max\nolimits_p\,\left\{
\left[ \begin{array}{c}
(c_k,\,x)\\...
...rray}\right]\ \mbox{$\,\mid\,$}\ Ax \le b,\ \ x \ge 0 \right\}
\end{displaymath}](img210.gif) |
(10.1) |
- задача лексикографической оптимизации, где p -
упорядочение функций
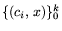 (или их индексов,
что одно и то же) по ''важности''. Для определенности можно считать
(или их индексов,
что одно и то же) по ''важности''. Для определенности можно считать
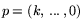 , т.е.
, т.е.
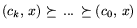 . Не приводя расшифровку смысла задачи
. Не приводя расшифровку смысла задачи
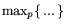 через лексикографическое упорядочение функций
через лексикографическое упорядочение функций
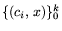 скажем, что задачу (10.1) можно понимать
как заключительную из задач:
скажем, что задачу (10.1) можно понимать
как заключительную из задач:
Задачи (10.1) и (10.2) эквивалентны в смысле
совпадения их оптимальных множеств. Это следует из смысла
лексикографического оптимума.
Если вместо вектора b взять матрицу
![$[b_0,\ b_1,\,...\,,b_l]$](img219.gif) и
положить
и
положить
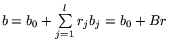 , то
задача (10.1) может быть переписана в следующем виде:
, то
задача (10.1) может быть переписана в следующем виде:
![\begin{displaymath}
L_p:\ \max\nolimits_p \left\{ \left[
\begin{array}{c}C^T x\\...
...ht]\ \mbox{$\,\mid\,$}\ Ax \leq b_0 + Br,\ \ x \ge 0 \right\},
\end{displaymath}](img221.gif) |
(10.3) |
выше
![$B = [b_1,\,...\,,b_l]$](img222.gif) ,
,
![$r^T = [r_1,\,...\,,r_l] \ge 0$](img223.gif) ,
,
![$C = [c_1,\,...\,,c_k]$](img224.gif) . Заметим, что повсюду, как и ранее,
предполагается столбцовая запись вектора.
. Заметим, что повсюду, как и ранее,
предполагается столбцовая запись вектора.
В качестве двойственного для (10.3) объекта можно естественным
образом записать задачу:
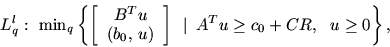 |
(10.4) |
где q - упорядочение функций
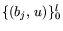 (или их индексов, что одно и то же),
(или их индексов, что одно и то же),
![$R^T = [R_1,\,...\,,R_k] \ge 0$](img227.gif) .
Для определенности можно считать
.
Для определенности можно считать
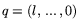 .
.
Симметрично скаляризовав (10.3) и (10.4) с помощью
векторных параметров 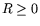 и
и 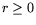 , соответственно,
получим пару взаимно сопряженных (в классическом смысле) задач ЛП:
, соответственно,
получим пару взаимно сопряженных (в классическом смысле) задач ЛП:
Связь между отмеченными четырьмя задачами может быть изображена
схемой:
В ней символ
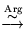 означает переход к новой
задаче с наследованием (сохранением) оптимального множества.
Точная формулировка факта такова.
означает переход к новой
задаче с наследованием (сохранением) оптимального множества.
Точная формулировка факта такова.
Теорема 10.1
Если задачи
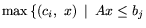
,
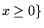
для всех
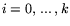
и
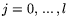
разрешимы, то существует непустая область конструктивно определяемых
параметров
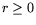
и
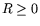
таких, что
Понятно, что
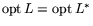
(теорема двойственности в ЛП).
11. Двойственность для несобственных
задач ЛП в лексикографической
интерпретации [58]
Пусть P и 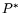 - задача из п. 9. Важным
является вопрос об аппроксимационном смысле задач P и
- задача из п. 9. Важным
является вопрос об аппроксимационном смысле задач P и 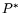 по отношению к L и
по отношению к L и 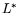 . Ниже этот смысл будет раскрыт
через термины лексикографической оптимизации.
. Ниже этот смысл будет раскрыт
через термины лексикографической оптимизации.
Будем исходить (в содержательном плане) из того, что системы
ограничений задач L и 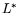 разбиты на подсистемы
разбиты на подсистемы 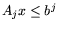
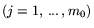 и
и
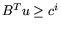
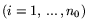 , причем неравенства из одной подсистемы не ранжируются,
а сами подсистемы ранжируются, например, в соответствии с такими
упорядочениями:
, причем неравенства из одной подсистемы не ранжируются,
а сами подсистемы ранжируются, например, в соответствии с такими
упорядочениями:
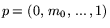 и
и
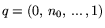 .
Введенному упорядочению можно придать следующий смысл: ограничения
.
Введенному упорядочению можно придать следующий смысл: ограничения
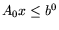 ,
, 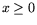 и
и
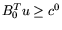 ,
, 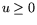 носят директивный характер и предполагаются совместными,
остальные - факультативными (в целом же они могут быть
несовместными). Однако в силу введенной упорядоченности подсистем их
невязки
носят директивный характер и предполагаются совместными,
остальные - факультативными (в целом же они могут быть
несовместными). Однако в силу введенной упорядоченности подсистем их
невязки
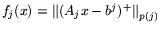
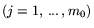 ,
,
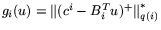
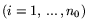 должно минимизировать последовательным образом в
соответствии с упорядочениями p и q. Как уже было
отмечено в предыдущем пункте, это эквивалентно постановке следующих
двух задач лексикографической оптимизации:
должно минимизировать последовательным образом в
соответствии с упорядочениями p и q. Как уже было
отмечено в предыдущем пункте, это эквивалентно постановке следующих
двух задач лексикографической оптимизации:
где M(r) и M#(R) - допустимые множества задач P и
P# соответственно. Предполагается, что функционалы 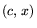 и
и
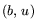 в упорядочениях p и q поставлены на последнее место.
в упорядочениях p и q поставлены на последнее место.
Теорема 11.1
Пусть нормы
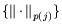
,
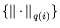
- монотонны вместе со своими сопряженными и
кусочно-линейны. Тогда существует непустая область конструктивно
определяемых
и
таких, что
12. Двойственность для дизъюнктивных задач
линейной оптимизации [52, 53, 63]
Дизъюнктивная задача МП - это задача поиска экстремума функции
на объединении конечной системы множеств, каждое из которых задано
некоторой системой неравенств:
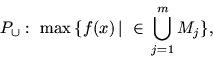 |
(12.1) |
где
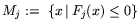 , Fj: R
, Fj: R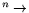 R
R
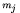 . Такой задаче можно поставить в соответствие дизъюнктивную функцию Ланранжа
. Такой задаче можно поставить в соответствие дизъюнктивную функцию Ланранжа
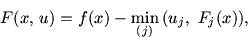 |
(12.2) |
с использованием которой можно связать построение двойственности
для задач типа (12.1). Важным оправдательным моментом этого
служит тот факт (достаточно простой), что если функция 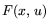 обладает седлом
обладает седлом
![$[\bar x,\,\bar u]$](img260.gif) , то
, то
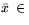
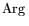 (12.1). Если постановка задачи (12.1)
линейная (или выпуклая), то можно формулировать теоремы
двойственности в разных формах, например, в форме теоремы
Куна-Таккера. Приведем пример. Пусть в (12.1):
(12.1). Если постановка задачи (12.1)
линейная (или выпуклая), то можно формулировать теоремы
двойственности в разных формах, например, в форме теоремы
Куна-Таккера. Приведем пример. Пусть в (12.1):
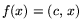 ,
,
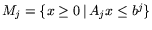 . Обозначим
эту задачу через
. Обозначим
эту задачу через  .
.
Теорема 12.1
Пусть задача
разрешима и
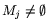
,
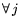
. Тогда дизъюнктивная функция Лагранжа
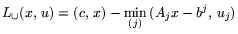
, отвечающая
задаче
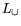
, обладает седлом
![$[\bar x,\,\bar u]$](img260.gif)
, причем в
качестве
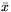
и
![$\bar u = [\bar{u}_1,\,...\,,\bar{u}_m]$](img268.gif)
выступают:
где
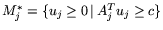
.
Подробное изложение двойственности для дизъюнктивных задач
линейного программирования см. в статье [
63], которая помещена
в настоящей книге.
13. Игровой подход к формированию стандартной двойственности
в нелинейном
программировании
Указанный подход аналогичен тому, который был изложен в пунктах
3 и 4, в связи с этим ниже имеют место некоторые
повторения.
Модель МП запишем в виде
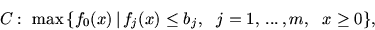 |
(13.1) |
где 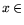 Rn. Этой постановке можно придать
следующий экономический смысл (аналогичный тому, который был изложен
в п. 1):
Rn. Этой постановке можно придать
следующий экономический смысл (аналогичный тому, который был изложен
в п. 1):
![$b^T = [b_1,\,...\,,b_m]$](img274.gif) - вектор
ресурсов, перерабатываемых в вектор продукции
- вектор
ресурсов, перерабатываемых в вектор продукции
![$x^T =
[x_1,\,...\,,x_n]$](img275.gif) ,
,
![$F^T (x) = [f_1(x),\,...\,,f_m(x)]$](img276.gif) - вектор
затрат ресурсов, необходимых для обеспечения производства продукции
уровня x, f0(x) - доход от реализации этой продукции. На
задачу C можно смотреть как на результат формализации
Производства - I-го игрока с множеством стратегий
- вектор
затрат ресурсов, необходимых для обеспечения производства продукции
уровня x, f0(x) - доход от реализации этой продукции. На
задачу C можно смотреть как на результат формализации
Производства - I-го игрока с множеством стратегий
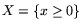 . Роль II-го игрока приписывается
Рынку с функциями поглощения продукции Производства по
фиксированной функции дохода, купле излишних (для I-го игрока)
ресурсов и продаже недостающих по ценам Рынка, формирующимся в
результате рыночного взаимодействия Производства и Рынка на основе принципа гарантированного результата. В
качестве платежной функции в описанной ситуации выступает функция Лагранжа
. Роль II-го игрока приписывается
Рынку с функциями поглощения продукции Производства по
фиксированной функции дохода, купле излишних (для I-го игрока)
ресурсов и продаже недостающих по ценам Рынка, формирующимся в
результате рыночного взаимодействия Производства и Рынка на основе принципа гарантированного результата. В
качестве платежной функции в описанной ситуации выступает функция Лагранжа
поставленная в соответствие задаче C. Здесь {uj}1m
- неотрицательные множители Лагранжа, играющие роль цен на
ресурсы. Принцип гарантированного результата формирует следующую
схему:
В этой схеме зафиксировано то обстоятельство, что максиминная задача (I-го игрока) эквивалентна исходной задаче C,
а минимаксная задача (II-го игрока) объявляется
двойственной.
Если
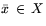 ,
,
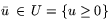 и
и
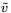 таковы, что
таковы, что
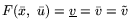 ,
то
,
то 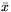 и
и 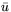 называются оптимальными
стратегиями I-го и II-го игроков соответственно, а
называются оптимальными
стратегиями I-го и II-го игроков соответственно, а 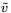 -
ценой игры. В нашей экономической интерпретации:
-
ценой игры. В нашей экономической интерпретации: 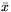 - оптимальный план Производства,
- оптимальный план Производства, 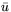 - вектор оптимальных
цен Рынка,
- вектор оптимальных
цен Рынка,
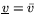 - фактор равновесия
Производства и Рынка (
- фактор равновесия
Производства и Рынка (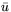 - вектор равновесных цен).
- вектор равновесных цен).
Справедлива
Теорема 13.1 (Куна-Таккера)
Пусть
C - разрешимая (в точке
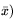
задача выпуклого
программирования, удовлетворяющая условию
Слейтера
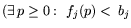
,
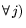
.
Тогда существует такой вектор
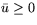
, что
![$[\bar{x},\ \bar{u}]
\,\in\,\mathrm{Arg}\,C^*$](img288.gif)
.
14. Принцип линеаризации в формировании
двойственности для нелинейных
задач МП [6]
В основе формирования 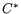 на основе принципа линеаризации
лежит следующая схема:
на основе принципа линеаризации
лежит следующая схема:
![\begin{displaymath}
\framebox[7cm][c]{$ C \stackrel {(l)}{\longrightarrow } L_p ...
...(p = x)}{\longrightarrow } L_x^{\ast} \equiv :\ C^{\ast} $}\ .
\end{displaymath}](img289.gif) |
(14.1) |
Здесь
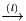 означает линеаризацию всех
функций, формирующих задачу C, в точке p (в результате
получается задача ЛП: Lp),
означает линеаризацию всех
функций, формирующих задачу C, в точке p (в результате
получается задача ЛП: Lp),
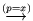 - это
операция автоматической замены p на
переменную x. Линеаризация в точке p произвольной
дифференцируемой функции f(x) состоит в замене ее линейной функцией
- это
операция автоматической замены p на
переменную x. Линеаризация в точке p произвольной
дифференцируемой функции f(x) состоит в замене ее линейной функцией
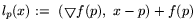 .
.
Если следовать этой схеме (в предположении дифференцируемости
функций
{fj(x)}0m), то задача C* из схемы (14.1)
примет вид:
где
![$F(x,\,u) = f_0(x) -\sum\limits_{j = 1}^m u_j\, [f_j(x) -b_j]$](img294.gif) .
Если в ограничениях задачи C нет требования
.
Если в ограничениях задачи C нет требования 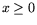 (обозначим ее C0), то
(обозначим ее C0), то 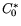 будет иметь несколько иной вид:
будет иметь несколько иной вид:
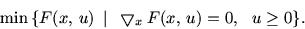 |
(14.2) |
Реализация схемы (14.1) может быть осуществлена и без
предположения гладкости задачи C (путем привлечения понятий суб-,
квази- и иной обобщенной дифференцируемости), но она (реализация)
будет выглядеть более громоздко.
В предположении выпуклости задачи C теорема двойственности
формулируется следующим образом:
Теорема 14.1
Если задача
C0 разрешима и удовлетворяет условию регулярности,
то задача
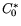
также разрешима и их оптимальные значения
совпадают.
Задачи C и 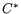 свойством взаимности не обладают,
поэтому в этом случае имеет смысл формулировать и обратную
теорему двойственности [6]:
свойством взаимности не обладают,
поэтому в этом случае имеет смысл формулировать и обратную
теорему двойственности [6]:
Теорема 14.2
Если задача
C0 разрешима, пусть в точке
![$[\bar x,\ \bar u]$](img297.gif)
,
и функция
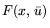
строго вогнута в некоторой окрестности
точки
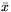
, то
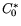
разрешима, при этом
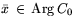
,
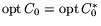
(т.е.
совпадение оптимальных значений).
Заметим, что условия оптимальности для задачи
C0 имеют вид
соотношений:
(условия Куна-Таккера), которые являются достаточными, а в
условиях прямой теоремы двойственности - и необходимыми.
З а м е ч а н и е 14.1. Рассмотренный выше принцип
линеаризации может быть применен к анализу любой проблемы нелинейного
программирования, формулируемой для того или иного подкласса задач
оптимизации, в частности тех, которые были рассмотрены в [67].
Если речь идет о проблеме формирования двойственности, например, для
несобственных задач нелинейного программирования, то это можно
осуществить на основе соединения схем 2 и (14.1).
Аналогичный подход можно реализовать и для других специальных задач
нелинейного программирования, для которых в предположении линейности
соответствующие вопросы уже нашли свое решение (например, вопрос о
формировании двойственности для лексикографических задач).
Разумеется, подход, основанный на применении принципа линеаризации,
еще не порождает справедливости аналога той или иной теоремы для
нелинейного случая, если эта теорема справедлива для случая
линейного. Речь идет только об идентификации образа этой
теоремы, ее формулировки.
15. Схема формирования двойственности для
несобственных задач нелинейного
программирования [23]
Приведенная схема на стр. ![[*]](crossref.gif) является соединением схем 2
и (14.1), о чем уже было сказано выше.
Схема не требует особых пояснений, так как все
необходимые разъяснения приведенных здесь символов имеются в
предыдущих пунктах. Если в качестве исходной задачи взять
является соединением схем 2
и (14.1), о чем уже было сказано выше.
Схема не требует особых пояснений, так как все
необходимые разъяснения приведенных здесь символов имеются в
предыдущих пунктах. Если в качестве исходной задачи взять
то в предположении дифференцируемости функций
{fj(x)}0m в полном соответствии со схемой 2 и ее последующей реализацией получаем:
Здесь
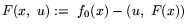 ,
,
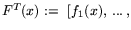
![$f_m(x)] = [F_0(x),\,...\,,F_{m_0}(x)]$](img310.gif) ;
;
![$c_x:=\ \bigtriangledown f_0(x) = \left[
\frac{\textstyle \partial f_0(x)}{\text...
...partial f_0 (x)}{\textstyle \partial x_n} \right]^T =
[c_x^1,\,...\,,c_x^{n_0}]$](img312.gif) .
.
Формулировки теорем двойственности для выписанных задач P и
P# могут быть даны только для частных случаев.
16. Некоторые замечания к общей схеме
формирования двойственности
Запишем задачу (13.1)
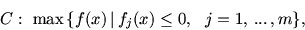 |
(16.1) |
не выделяя специально условие 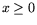 (если в конкретной
задаче таковое присутствует, то оно может быть учтено в общем списке
ограничений в форме неравенств
(если в конкретной
задаче таковое присутствует, то оно может быть учтено в общем списке
ограничений в форме неравенств 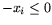 ,
,
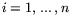 ).
Запишем двойственную к ней задачу
).
Запишем двойственную к ней задачу
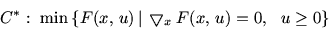 |
(16.2) |
(см. (14.2)). На формирование двойственности в силу
отображения
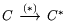 можно смотреть как на
универсальную схему, распространяющуюся на оптимизационные
задачи и из других разделов математики (математическая экономика,
оптимальное управление, приближение функций и др.). Схема работает,
естественно, и для задач ЛП. Проиллюстрируем это на задаче
можно смотреть как на
универсальную схему, распространяющуюся на оптимизационные
задачи и из других разделов математики (математическая экономика,
оптимальное управление, приближение функций и др.). Схема работает,
естественно, и для задач ЛП. Проиллюстрируем это на задаче
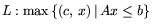 . Запишем для нее функцию Лагранжа
. Запишем для нее функцию Лагранжа
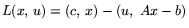 ,
, 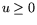 . С помощью
элементарных преобразований ее можно переписать в виде
. С помощью
элементарных преобразований ее можно переписать в виде
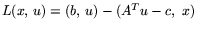 . Тогда двойственная к L задача L* по
схеме (16.2) запишется так:
. Тогда двойственная к L задача L* по
схеме (16.2) запишется так:
что эквивалентно задаче
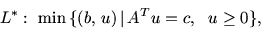 |
(16.3) |
что и требовалось.
Проиллюстрируем обсуждаемую схему еще одним весьма важным
примером, а именно примером задачи, регуляризирующей (по Тихонову)
задачу L :
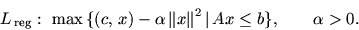 |
(16.4) |
Запишем для
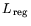 ее функцию Лагранжа
ее функцию Лагранжа
и ее градиент
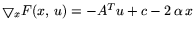 . Двойственная к
. Двойственная к
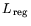 задача
задача
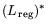 запишется по правилу (16.2) в форме:
запишется по правилу (16.2) в форме:
или путем замены
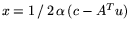 :
:
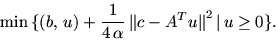 |
(16.5) |
Итак, в качестве двойственной к
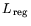 мы получим
задачу (16.5), обозначенную
мы получим
задачу (16.5), обозначенную
 . Последняя
является ничем иным как задачей, реализующей метод квадратичных
штрафных функций, примененным к задаче (16.3) со штрафной
константой
. Последняя
является ничем иным как задачей, реализующей метод квадратичных
штрафных функций, примененным к задаче (16.3) со штрафной
константой
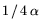 . Обозначим задачу (16.5) символом
. Обозначим задачу (16.5) символом
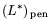 . Нами показано
. Нами показано
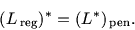 |
(16.6) |
На самом деле реализуется схема:
В нижней части этой схемы переход
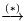 соответствует проверенному соотношению (16.6). Верен и обратный
переход
соответствует проверенному соотношению (16.6). Верен и обратный
переход
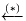 , однако его обоснование требует
специального подхода, базирующегося на искусственном преобразовании
задачи (16.5). Это преобразование состоит в замене c-AT u =
w и перезаписи задачи в форме
, однако его обоснование требует
специального подхода, базирующегося на искусственном преобразовании
задачи (16.5). Это преобразование состоит в замене c-AT u =
w и перезаписи задачи в форме
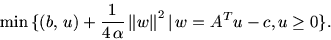 |
(16.7) |
Функцией Лагранжа для этой задачи (с учетом в ней ограничения 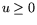 ) будет
) будет
где x - вектор множителей Лагранжа, соответствующий
векторному уравнению w = AT u - c; 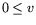 - аналогичный
вектор для
- аналогичный
вектор для 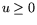 . Двойственной к (16.5) (следовательно, и
к (16.7)) будет задача
. Двойственной к (16.5) (следовательно, и
к (16.7)) будет задача
![\begin{displaymath}
\max\,\{ F(u, w;\ x, v) \mbox{$\,\mid\,$}\bigtriangledown _{[u, w]} F(u, w;\ x, v) = 0,
v \ge 0 \}.
\end{displaymath}](img339.gif) |
(16.8) |
Вычисляем
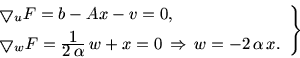 |
(16.9) |
С учетом (16.9) преобразуем функцию Лагранжа:
Таким образом, применяя к (16.5) схему формирования
двойственной задачи, мы получим задачу
т.е.
а это - задача
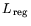 . Следовательно, мы
проверили соотношение
. Следовательно, мы
проверили соотношение
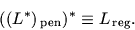 |
(16.10) |
Наравне со схемой 6 можно выписать ей симметричную схему:
в соответствии с которой справедливо соотношение
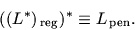 |
(16.11) |
Задачи
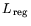 и
и
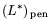 связаны
между собой классической теоремой двойственности (вытекает из
обоснования схемы 6 и теоремы 13.1).
связаны
между собой классической теоремой двойственности (вытекает из
обоснования схемы 6 и теоремы 13.1).
Теорема 16.1
Задачи
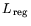
и
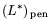
одновременно разрешимы или неразрешимы, при этом в случае
разрешимости
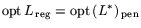
.
П р и м е ч а н и е. Естественно, это утверждение
верно и для пары задач
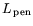 ,
,
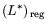 .
.
Выпишем тройку задач:
Отметим связи между ними (при разрешимости
L):
- 1)
-
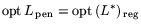 (теорема двойственности);
(теорема двойственности);
- 2)
-
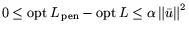 ,
,
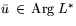 ;
;
- 3)
- при достаточно малом
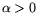 оптимальный вектор
оптимальный вектор 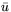 задачи
задачи
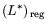 является минимальным по норме
оптимальным вектором задачи L*.
является минимальным по норме
оптимальным вектором задачи L*.
Следствие. Пусть L разрешима. Тогда при достаточно
малом
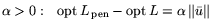 .
.
Заметим, что для задачи L в качестве
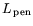 чаще
записывают задачу:
чаще
записывают задачу:
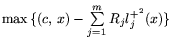 , где lj(x) - левые части системы
, где lj(x) - левые части системы
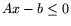 , Rj > 0,
, Rj > 0,
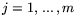 . В этом случае оценка 2) и
соотношение из следствия принимают вид:
. В этом случае оценка 2) и
соотношение из следствия принимают вид:
и
- при достаточно большом
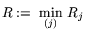
.
Выше было выявлено для линейного случая свойство взаимной сопряженности
метода регуляризации Тихонова и метода квадратичных штрафных функций.
Что касается нелинейных задач математического программирования,
то этот вопрос требует своих исследований. Выявленную при этом
симметрию (для линейного случая) ожидать в нелинейной ситуации не
приходится. Однако для задач квадратичного программирования этот
вопрос можно считать решенным [65].
ЛИТЕРАТУРА
- Wolfe P. A Duality Theorem for Nonlinear
Programming. Quarterly of Applied Mathematics, 1961,
19, pp. 239-244.
- Mangasarian O.L. Duality in Nonlinear
Programming. Quarterly of Applied Mathematics, 1962,
20, pp. 300-302.
- Charnes A., Cooper W.W., Kortanek K.O. A Duality
Theory for Convex Programs with Convex Constraints. Bull. American
Mathematical Society, 1962, 68, pp. 605-608.
- Mangasarian O.L., Ponstein J. Minimax and Duality
in Nonlinear Programming. J. Mathematical Analysis and
Applications, 1965, 11, pp. 504-518.
- Kuhn H.W. Duality in Mathematical Programming.
Mathematical Systems Theory and Economics (Lecture Notes in
Operations Research and Mathematical Economics,
11), 1969, New York: Springer-Verlag, pp. 67-91.
- Mangasarian O.L. Optimality and Duality in Nonlinear
Programming. In Proceedings of Princeton Simposium on Mathematical
Programming (Ed. Kuhn H.W.), 1970, pp. 429-443.
- Bazaraa M.S. Geometry and Resolution of Duality
Gaps. Naval Research Logistics Quarterly, 1973, 20,
pp. 357-365.
- Гольштейн Е.Г. Теория двойственности в
математическом программировании и ее приложения. М.: Наука, 1971,
352 с.
- Астафьев Н.Н. Линейные неравенства и выпуклость.
М.: Наука, 1982, 152 с.
- Evers J.J.&H. van Maaren. Duality Principes in
Mathematics and Their Relations to Conjugate Functions. Nieuw arohiff
voor wiskunde (4), 1985, v. 3.
- Еремин И.И. О методе штрафов в выпуклом
программировании. Кибернетика, 1967, 4, 4 c.
- Еремин И.И. Метод штрафов в выпуклом
программировании. ДАН СССР, 1967, 4, 4 c.
- Еремин И.И., Астафьев Н.Н. Двойственность в
выпуклом программировании. Книга ''Методы управления большими
системами'', 1970, 1, 25 c.
- Еремин И.И. О задачах последовательного
программирования. Сибирский матем. журнал, 1973, т. 14,
1, 10 c.
- Еремин И.И., Астафьев Н.Н. Введение в теорию
линейного и выпуклого программирования. М.: изд-во физ.-мат.
литературы, 1976, 192 c.
- Еремин И.И., Мазуров Вл.Д. Нестационарные
процессы математического программирования. М.: Наука, 1979,
288 c.
- Еремин И.И. Двойственность для несобственных
задач линейного и выпуклого программирования. ДАН СССР, 1981,
т. 256, 2, 5 c.
- Eremin I.I. Duale uneigentliche lineare und
Konvexe Optimierungeprobleme. Math. Operationsforsch.
Statist., Ser. Optimization, 1982, v. 13, 2,
12 p.
- Еремин И.И. Двойственность для несобственных
задач линейного программирования. Сб. ''Несобственные задачи
оптимизации''. Свердловск: УНЦ АН СССР, 1982, 8 c.
- Еремин И.И. Двойственность для несобственных
задач линейного программирования. Матем. заметки, 1982, т. 32,
вып. 2, 11 c.
- Еремин И.И. О двойственности для несобственных
задач линейного и выпуклого программирования. Труды 27 Междунар.
научного коллоквиума. Берлин, Высшая техническая школа Ильменау,
1982, тетрадь 5, 3 c.
- Еремин И.И. Двойственность для несобственных
задач линейного и выпуклого программирования и методы их коррекции.
Изв. АН СССР. Техн. кибернетика, I, 1983, 12 c.
- Еремин И.И., Мазуров Вл.Д., Астафьев Н.Н.
Несобственные задачи линейного и выпуклого программирования.
М.: Наука, 1983, 336 c.
- Еремин И.И. Двойственность для несобственных
задач квадратичного программирования. Тезисы докладов конф.
''Методы математического программирования и их программное
обеспечение''. Свердловск: УНЦ АН СССР, 1984, 2 c.
- Еремин И.И., Ватолин А.А. Двойственность для
несобственных бесконечномерных задач линейного и выпуклого
программироания. Сб. ''Методы аппроксимации несобственных задач
математического программироания''. Свердловск: УНЦ АН СССР, 1984,
17 c.
- Еремин И.И., Ватолин А.А. Двойственность для
несобственных задач математического программирования в условиях
информационной неопределенности. Тезисы докладов Междунар. конф.
''Стохастическая оптимизация'' (часть I). Киев, 1984, 1 c.
- Еремин И.И. Вопросы двойственности для несобственных
задач математического программирования. Алгебра и логика.
Новосибирск, 1984, т. 23, 6, c. 624-635.
- Еремин И.И. Несобственные задачи квадратичного
программирования и вопросы регуляризации. Сб. ''Параметрическая
оптимизация и методы аппроксимации несобственных задач
математического программирования''.
Свердловск: УНЦ АН СССР, 1985, c. 47-50.
- Eremin I.I. Parametrization methods in the analysis
of improper mathematical programming problems. Abstracts
International Conference ''Parametric Optimization and
Related Topics''. Plane / Thüringen, GDR, 1985,
pp. 10-11.
- Еремин И.И., Ватолин А.А. Двойственность для
несобственных задач математического программирования.
Свердловск: УНЦ АН СССР, 1985, 50 c.
- Еремин И.И. Противоречивые модели экономики.
Свердловск: Средне-Уральское книж. изд-во, 1986, 96 c.
- Eremin I.I. Duality and the correcting methods
for ill-posed of linear and convex programming.
Seminarber., Humboldt-Univ. Berlin. Sekt. Math. 81,
1986, pp. 27-45.
- Eremin I.I., Vatolin A.A. Duality in
improper mathematical programming problems under
uncertainty. Stochastic optimization. Prac. Int. Conf.
Kiev / USSR, 1984. Lect. Notes Control Inf. Sci. 81, 1986,
pp. 326-333.
- Еремин И.И. О двойственности в линейной векторной
оптимизации. Тезисы докладов конф. ''Методы математического
программирования и программное обеспечение''. Свердловск: УНЦ АН
СССР, 1987, c. 41-42.
- Eremin I.I. Methods of Parametrization in the
Analysis of Improper Mathematical Programming Problems.
Parametric Optimization and Related Topics. Akademie-Verlag
Berlin, 1987, pp. 82-94.
- Еремин И.И. Вопросы двойственности для несобственных
задач многокритериальной линейной оптимизации. Сб. ''Исследования по
несобственным задачам оптимизации''. Свердловск: УрО АН
СССР, 1988, c. 27-33.
- Еремин И.И. Симметрическая двойственность в линейной
векторной оптимизации. Тезисы докладов Междунар. конф.
''Многокритериальные задачи математического
программирования''. Киев, 1988, c. 6-7.
- Еремин И.И. Двойственность для противоречивых задач
оптимальной линейной дискриминации. Тезисы докладов конф. ''Численные
методы и оптимизация''. Таллинн, 1988, c. 81-87.
- Еремин И.И. Общая схема формирования
двойственности для несобственных задач математического
программирования. Кибернетика, 1989, 5, c. 79-82.
- Eremin I.I., Vatolin A.A. Improper Mathematical
Programming Problems. Problems of Control and Information Theory,
1989, v. 18(6), pp. 359-380.
- Еремин И.И. Симметричная двойственность для
лексикографической постановки задачи линейного программирования.
Тезисы докладов конф. ''Математическое программирование и приложения''.
Свердловск: УрО АН СССР, 1991, c. 58-59.
- Еремин И.И. Симметричная двойственность для задач
последовательного линейного программирования. ДАН СССР, 1991,
т. 317, 5, c. 1045-1048.
- Eremin I.I. Lexicographic duality in linear
optimization. Proceedings of International Workshop on
Computationally-intensive Methods in Simulation and
Optimization. Wien, 1991, pp. 8-11.
- Еремин И.И., Ватолин А.А., Попов Л.Д., Третьяков Н.В.
Несобственные задачи математического программирования.
Математические методы в
экономико-математическом моделировании.
М.: Наука, 1991.
- Еремин И.И. Двойственность в математическом
программировании. Информ. бюлл. АМП. Екатеринбург: УрО РАН,
1992, 3, c. 11-30.
- Еремин И.И. Симметрическая двойственность для
лексикографических задач линейного программирования. Украинский
матем. журнал, 1992, т. 44, 6, c. 766-773.
- Еремин И.И. Лексикографическая двойственность для
несобственных задач линейного и квадратичного программирования.
Труды ИММ УрО РАН. Екатеринбург: УрО РАН, 1992, т. I,
c. 178-192.
- Еремин И.И., Жан-Гериев А.А. Двойственность для
полупаретовской постановки задачи линейного программирования. Информ.
бюлл. АМП. Екатеринбург: УрО РАН, 1993, 4, c. 46.
- Еремин И.И. Лексикографическая двойственность в
математическом программировании. Тезисы докладов Междунар. семинара
''Негладкие и разрывные задачи управления и оптимизации''. Челябинск,
1993, c. 54-55.
- Еремин И.И. Двойственность для
парето-лексикографических
задач линейной оптимизации. Известия ВУЗов. Математика. Казань:
изд-во ФОРТ ДИАЛОГ, 1993, 12(379), c. 3-10.
- Eremin I.I. Duality for Pareto-Lexicographic Problems
of Linear Optimization. Pattern Recognition and Image Analysis, 1993,
v. 3, 4, pp. 482-487.
- Еремин И.И. Парето-последовательная задача
линейной оптимизации и двойственность. Доклады РАН,
1994, т. 334, 4, c. 141-143.
- Eremin I.I. Summetric Duality in Lexicographic
Problems of Linear Optimization. Yugoslav Journal of Operations
Research. Belgrade: University of Belgrade, 1995, v. 5,
2, pp. 165-172.
- Еремин И.И. Двойственность для задач дискриминации и
таксономии систем линейных неравенств. Pattern Recognition and Image
Analysis, 1995, 3, c. 233-236.
- Еремин И.И. Двойственность для
Парето-последовательных
задач линейного программирования. Труды ИММ УрО РАН. Екатеринбург:
УрО РАН, 1995, т. III, c. 245-261.
- Еремин И.И. Двойственность для
Парето-последовательных
задач линейного программирования. Управление. Оптимизация.
Интеллект. Иркутск: СЭИ СО РАН, 1995, 1, c. 3-19.
- Еремин И.И. Двойственность в несобственном
программировании. Кибернетика и системный анализ, 1996, 6,
13 c.
- Еремин И.И. Двойственность для несобственных задач
паретовской и лексикографической линейной оптимизации. Труды ИММ
УрО РАН. Екатеринбург: УрО РАН, 1996, т. IV, c. 322-336.
- Еремин И.И. Двойственность для несобственных задач
линейной оптимизации. Информ. бюлл. АМП. Екатеринбург: УрО РАН,
1996, 6, c. 32-37.
- Еремин И.И. Двойственность для кусочно-линейных
задач оптимизации. Информ. бюлл. АМП. Екатеринбург: УрО РАН, 1997,
7, c. 88-89.
- Eremin I.I. About some problems of disjunctive
programming. Yugoslav Journal of Operations Research. Belgrade:
University of Belgrade, 1998, v. 8, 1,
pp. 25-43.
- Еремин И.И. Сигма-кусочные функции и задачи
дизъюнктивного программирования. Доклады РАН, 1998, т. 358, 5,
c. 538-540.
- Еремин И.И. Сигма-кусочные функции и задачи
дизъюнктивного программирования. Труды ИММ УрО РАН.
Екатеринбург: УрО РАН, 1998, т. V, c. 357-380.
- Еремин И.И. Теоремы о седловой точке дизъюнктивной
функции Лагранжа. Алгоритмический анализ некорректных задач.
Тезисы докл. конф., 1998 г. Екатеринбург: УрГУ, 1998,
c. 85-86.
- Еремин И.И. О квадратичных и полноквадратичных
задачах выпуклого программирования. Известия ВУЗов. Математика.
Казань: изд-во ФОРТ ДИАЛОГ, 1998, 12, c. 22-28.
- Еремин И.И. Двойственность для задач квадратичного
программирования в гильбертовом пространстве. Информ. бюлл.
АМП. Екатеринбург: УрО РАН, 1999, 8, c. 99-102.
- Еремин И.И. Теория линейной оптимизации. Екатеринбург: Изд-во ''Екатеринбург'', 1999, 312 c.


Next: II Лексикографическая двойственность для
Up: book
Previous: book
Список научных трудов Еремина И.И.
e-mail: Еремин И.И.
![]() - некоторый исходный математический объект
(модель), то двойственный объект
- некоторый исходный математический объект
(модель), то двойственный объект
![]() , вообще говоря,
выступает как некий внешний по отношению к
, вообще говоря,
выступает как некий внешний по отношению к ![]() объект ''наблюдения'' за
объект ''наблюдения'' за ![]() . Конечно, двойственность в
зависимости от ее конкретного содержания, определяемого конкретной
математической дисциплиной (алгебра, функциональный анализ, выпуклый
анализ, теория оптимального управления и т.д.), несет в себе следы
специфики соответствующей дисциплины. Но именно это обстоятельство и
превращает двойственность в математике в здание хотя в определенном
смысле и единой, но гармонически организованной и насыщенной
архитектуры.
. Конечно, двойственность в
зависимости от ее конкретного содержания, определяемого конкретной
математической дисциплиной (алгебра, функциональный анализ, выпуклый
анализ, теория оптимального управления и т.д.), несет в себе следы
специфики соответствующей дисциплины. Но именно это обстоятельство и
превращает двойственность в математике в здание хотя в определенном
смысле и единой, но гармонически организованной и насыщенной
архитектуры.
![]() , формируемой по определенным правилам и
называемой двойственной. Эти задачи связаны математически
содержательными соотношениями, позволяющими, например, получить
оценки критериальной эффективности всех параметров, формирующих
задачу C; свести решение оптимизационной задачи к решению некоторой
системы неравенств; сформировать в изящной форме условия
оптимальности; оценить скорость сходимости итерационных процессов для
задачи C и т.д.
, формируемой по определенным правилам и
называемой двойственной. Эти задачи связаны математически
содержательными соотношениями, позволяющими, например, получить
оценки критериальной эффективности всех параметров, формирующих
задачу C; свести решение оптимизационной задачи к решению некоторой
системы неравенств; сформировать в изящной форме условия
оптимальности; оценить скорость сходимости итерационных процессов для
задачи C и т.д.
![]() системы исходных ингредиентов
системы исходных ингредиентов
![]() обладающих ценностью, в новую систему
носителей ценности - совокупность продуктов. Термины
производство, ценность, продукт, а ниже - оценка (как
измеритель ценности) будут употребляться в качестве исходных.
обладающих ценностью, в новую систему
носителей ценности - совокупность продуктов. Термины
производство, ценность, продукт, а ниже - оценка (как
измеритель ценности) будут употребляться в качестве исходных.
![]() . В этом
предположении затраты j-го ингредиента, отнесенные к вектору x,
выразятся величиной
. В этом
предположении затраты j-го ингредиента, отнесенные к вектору x,
выразятся величиной ![]() ,
, ![]() . Так как границы
сверху для них определены числами bj, то должны выполняться
неравенства
. Так как границы
сверху для них определены числами bj, то должны выполняться
неравенства
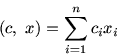
![]() максимальное значение.
максимальное значение.
![]() выражает доход от реализации продукции, который максимизируется.
выражает доход от реализации продукции, который максимизируется.
![]() ,
,
![]() , ситуацию модели (1.2)
можно изобразить геометрически: см. Рис. 1.
, ситуацию модели (1.2)
можно изобразить геометрически: см. Рис. 1.
![\begin{picture}(110.00,125.00)(0,0)
\put(5.0,10.0){\thicklines\vector(1,0){100.0...
...put(80,10){\line(0,1){28}}
}
\put(60,-7){\makebox(0,0)[c]{Рис.~1}}
\end{picture}](img38.gif)
![]() ,
, ![]() - вектор оптимального уровня производства, отвечающий направлению
изображенного вектора c. Многогранники M и N выступают в
качестве областей ''ресурсных возможностей'' и ''потребностей''.
На практике, да и в общем смысле (в соответствии с аксиомами
''общества потребления''), многогранники M и N находятся в
состоянии ''противостояния'', несогласованности, что можно выразить
пустотой их пересечения:
- вектор оптимального уровня производства, отвечающий направлению
изображенного вектора c. Многогранники M и N выступают в
качестве областей ''ресурсных возможностей'' и ''потребностей''.
На практике, да и в общем смысле (в соответствии с аксиомами
''общества потребления''), многогранники M и N находятся в
состоянии ''противостояния'', несогласованности, что можно выразить
пустотой их пересечения:
![]() .
.
![]() и
и
![]() , означающими выигрыши игроков при независимом выборе ими
стратегий
, означающими выигрыши игроков при независимом выборе ими
стратегий ![]() и
и ![]() . Если
. Если
![]() , т.е. выигрыш 1-го игрока равен проигрышу 2-го, то игра
называется игрой с нулевой суммой. В случае такой игры можно
оперировать лишь функцией выигрыша 1-го игрока
, т.е. выигрыш 1-го игрока равен проигрышу 2-го, то игра
называется игрой с нулевой суммой. В случае такой игры можно
оперировать лишь функцией выигрыша 1-го игрока
![]() , она же - функция проигрыша для 2-го игрока. Одним из
важнейших принципов анализа такой игры является принцип гарантированного результата. Он направлен на отыскание игроками
стратегий, обеспечивающих гарантированные выигрыши. Формализацию
такого подхода можно осуществить путем следующих рассуждений. Если
1-ый игрок зафиксирует свою стратегию
, она же - функция проигрыша для 2-го игрока. Одним из
важнейших принципов анализа такой игры является принцип гарантированного результата. Он направлен на отыскание игроками
стратегий, обеспечивающих гарантированные выигрыши. Формализацию
такого подхода можно осуществить путем следующих рассуждений. Если
1-ый игрок зафиксирует свою стратегию ![]() , то он может
подсчитать свой гарантированный выигрыш
, то он может
подсчитать свой гарантированный выигрыш
![]() , а затем его максимизировать,
т.е. подсчитать
, а затем его максимизировать,
т.е. подсчитать
![\begin{picture}(135,55)(0,0)
\put (35,30){\framebox (50,10)[c]{Производство}}
...
...х влево
\put (105,35){\vector(-3,-2){29.5}} % < 45 вниз влево
\par\end{picture}](img56.gif)
![]() En, а Рынок - в
роли 2-го игрока с функциями: 1) поглощение продукции Производства по фиксированным ценам ci,
En, а Рынок - в
роли 2-го игрока с функциями: 1) поглощение продукции Производства по фиксированным ценам ci, ![]() и
2) поглощение (покупка) или продажа ресурсов по ценам игрового
взаимодействия в системе ''Производство - Рынок''. Множеством
стратегий ''Рынка'' будет совокупность ценовых векторов
и
2) поглощение (покупка) или продажа ресурсов по ценам игрового
взаимодействия в системе ''Производство - Рынок''. Множеством
стратегий ''Рынка'' будет совокупность ценовых векторов
![]() Em, т.е. uj - цена единицы ресурса с
номером j,
Em, т.е. uj - цена единицы ресурса с
номером j, ![]() . В роли платежной функции в данной игре
выступает
. В роли платежной функции в данной игре
выступает
![\begin{displaymath}(=(c,\ x) -\sum_{j=1}^{m} u_j\, [(a_j,\ x) -b_j]),\end{displaymath}](img61.gif)
![]() - двойственной к L, может быть
реализован путем установления следующих эквивалентных переходов
- двойственной к L, может быть
реализован путем установления следующих эквивалентных переходов
![]() :
:
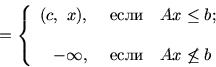
![]() . Имеем
. Имеем
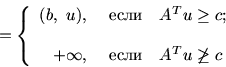
![]() и
и ![]() в двух формах:
в двух формах:
![\begin{displaymath}\left. \begin{array}{l}
P_1:\ \max f(x)\\ [4pt]
\qquad f_j(...
...\\ [4pt]
\qquad x\geq 0
\end{array}\right \} \rightleftarrows\end{displaymath}](img89.gif)
![\begin{displaymath}\rightleftarrows
\begin{array}{l}\\ [4pt]
F_1(x,\ u) =f(x) ...
...m} u_j f_j(x),\\ [4pt]
u_j\geq 0,\ \ \forall \,j,
\end{array}\end{displaymath}](img90.gif)
![\begin{displaymath}\left. \begin{array}{l}
P_2:\ \min f(x)\\ [4pt]
\qquad f_j(...
...\\ [4pt]
\qquad x\geq 0
\end{array}\right \} \rightleftarrows\end{displaymath}](img91.gif)
![\begin{displaymath}\rightleftarrows
\begin{array}{l}\\ [4pt]
F_2(x,\ u) =f(x) ...
...m} u_j f_j(x),\\ [4pt]
u_j\geq 0,\ \ \forall \,j.
\end{array}\end{displaymath}](img92.gif)
![\begin{displaymath}F_1(x,\ u) \,\longrightarrow \, \left \{ \begin{array}{l}
P_...
...uad j=1,\,...\,,m,\\ [4pt]
\qquad x\geq 0
\end{array}\right .\end{displaymath}](img96.gif)
![\begin{displaymath}F_2(x,\ u) \,\longrightarrow \, \left \{ \begin{array}{l}
P_...
...ad j=1,\,...\,,m,\\ [4pt]
\qquad x\geq 0.
\end{array}\right .\end{displaymath}](img97.gif)
![\begin{picture}(150,120)(0,0)
\put (20,10){\framebox (40.3,20)[c]{}}
\put (80,...
...0){\makebox(0,0)[c]{$(\ast)$}}
\put (123,20){\makebox(0,0)[c]{.}}
\end{picture}](img101.gif)
![]() к двойственной задаче в
верхней строчке схемы согласуется с правилом перехода
к двойственной задаче в
верхней строчке схемы согласуется с правилом перехода ![]() в
нижней строчке.
в
нижней строчке.
![]() En+ - подлежащий определению вектор энергетических
измерителей исходных ингредиентов, то высказанная аксиома может быть
выражена неравенством
En+ - подлежащий определению вектор энергетических
измерителей исходных ингредиентов, то высказанная аксиома может быть
выражена неравенством
![]() . В частности, если
h=hi - i-ый столбец матрицы A, выражающий расход
ингредиентов на единицу продукции i-го вида и оцениваемый
величиной ci, то выписанное неравенство примет вид
. В частности, если
h=hi - i-ый столбец матрицы A, выражающий расход
ингредиентов на единицу продукции i-го вида и оцениваемый
величиной ci, то выписанное неравенство примет вид
![]() .
.
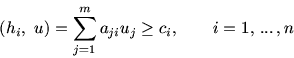
![]() употребленный термин
''энергетическая оценка'' имеет чисто ассоциативный смысл, и
большего в него вкладывать не следует (по крайней мере в рамках
данного кратко изложенного подхода к формированию двойственности
в ЛП).
употребленный термин
''энергетическая оценка'' имеет чисто ассоциативный смысл, и
большего в него вкладывать не следует (по крайней мере в рамках
данного кратко изложенного подхода к формированию двойственности
в ЛП).
![]() L - оптимальное
множество задачи L,
L - оптимальное
множество задачи L,
![]() L - конкретный элемент из
L - конкретный элемент из
![]() L,
L,
![]() L - оптимальное значение задачи L. Если S - символ
для обозначения некоторой системы линейных неравенств, то
L - оптимальное значение задачи L. Если S - символ
для обозначения некоторой системы линейных неравенств, то
![]() S
будет означать множество ее решений. Отметим очевидные соотношения:
S
будет означать множество ее решений. Отметим очевидные соотношения:
![]() вытекает разрешимость L и совпадение их
оптимальных значений.
вытекает разрешимость L и совпадение их
оптимальных значений.
![]() поставим в
соответствие систему линейных неравенств
поставим в
соответствие систему линейных неравенств
![]() в форме (7.1),
(7.1)
в форме (7.1),
(7.1)![]() и системой S устанавливает
и системой S устанавливает
![]() при
задании L в самом общем виде.
при
задании L в самом общем виде.
![\begin{figure}\begin{displaymath}\begin{array}{lllll}
L: &\max\,(c,\ x) &
\stac...
...\ [8pt]
\quad\, j\in J_0.
\end{array} \end{array}\end{displaymath}\end{figure}](img133.gif)
![]() (см. п. 4), переменный вектор
(см. п. 4), переменный вектор ![]() выступает как вектор
допустимых цен на ресурсы в игре ''Производство-Рынок'', а
оптимальный вектор цен
выступает как вектор
допустимых цен на ресурсы в игре ''Производство-Рынок'', а
оптимальный вектор цен
![]() в силу
эквивалентности (4.2) как оптимальный вектор задачи
в силу
эквивалентности (4.2) как оптимальный вектор задачи ![]() .
Таким образом, задача L как модель производства с фиксированными
ценами на продукт дополняется моделью определения оптимальных цен
(двойственных оценок) на ресурсы.
.
Таким образом, задача L как модель производства с фиксированными
ценами на продукт дополняется моделью определения оптимальных цен
(двойственных оценок) на ресурсы.
![]() , где
, где
![]() L,
L,
![]()
![]()
![]() . По теореме двойственности
. По теореме двойственности
![]() (
(
![]() ), т.е. при оптимальном плане
), т.е. при оптимальном плане ![]() Производства и
оптимальных ценах
Производства и
оптимальных ценах ![]() на ресурсы схема, изображенная на
стр.
на ресурсы схема, изображенная на
стр. ![[*]](crossref.gif) ,
работает с коэффициентом полезного действия,
равным единице. Заметим, что расширительного толкования этому
факту придавать не следует.
,
работает с коэффициентом полезного действия,
равным единице. Заметим, что расширительного толкования этому
факту придавать не следует.
![]() optL, где L -- произвольная задача ЛП,
optL, где L -- произвольная задача ЛП,
![]() .
.
![]() по произвольному направлению l из пространства вектора y.
Примем в качестве l вектор
по произвольному направлению l из пространства вектора y.
Примем в качестве l вектор
![]() .
Частный случай этой ситуации реализуется соотношением
.
Частный случай этой ситуации реализуется соотношением
![]() в качестве аргумента
ниже будем ставить тот фрагмент информационного вектора, который нас
интересует:
в качестве аргумента
ниже будем ставить тот фрагмент информационного вектора, который нас
интересует: ![]() ,
,
![]() и т.д.
и т.д.
![]() ,
, ![]() . В случае
единственности оптимального вектора
. В случае
единственности оптимального вектора ![]() задачи
задачи ![]() существует окрестность v(b) вектора
существует окрестность v(b) вектора
![]() (V0
- внутренность множества V) такая, что
(V0
- внутренность множества V) такая, что
![]() и
и
![]() - допустимые
множества для пары взаимно двойственных задач ЛП, например, в
форме (1.1), то (как уже отмечалось) непустота M и
- допустимые
множества для пары взаимно двойственных задач ЛП, например, в
форме (1.1), то (как уже отмечалось) непустота M и
![]() соответствует разрешимости этих задач. В случае
неразрешимости L (следовательно, и
соответствует разрешимости этих задач. В случае
неразрешимости L (следовательно, и ![]() ) возможны три
альтернативы:
) возможны три
альтернативы:
![\begin{figure}\begin{displaymath}
\begin{array}{rcc}
L & \stackrel {\pi}{\longr...
...ar93 }\,. \\ [18pt]
& \mbox{Схема 2} &
\end{array} \end{displaymath}\end{figure}](img173.gif)
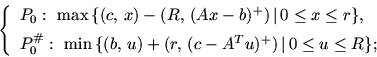
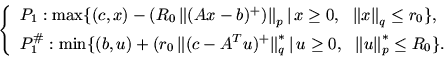
![]()
![]() и
и
![]()
![]() - произвольные разбиения систем
- произвольные разбиения систем ![]() и
и
![]() на
подсистемы (в предположении, что подсистемы
на
подсистемы (в предположении, что подсистемы ![]() ,
, ![]() и
и
![]() ,
, ![]() - совместны); {bj},
{uj}, {ci}, {xi} - разбиения векторов
- совместны); {bj},
{uj}, {ci}, {xi} - разбиения векторов ![]() на подвекторы, соответствующие указанному разбиению. В
принятых обозначениях задачи P и P# могут быть записаны
следующим образом:
на подвекторы, соответствующие указанному разбиению. В
принятых обозначениях задачи P и P# могут быть записаны
следующим образом:
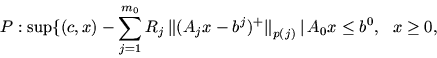
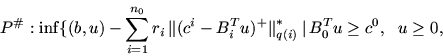
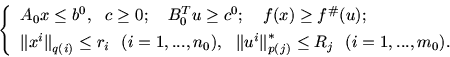
![]() и
положить
и
положить
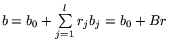 , то
задача (10.1) может быть переписана в следующем виде:
, то
задача (10.1) может быть переписана в следующем виде:
![]() и
и ![]() , соответственно,
получим пару взаимно сопряженных (в классическом смысле) задач ЛП:
, соответственно,
получим пару взаимно сопряженных (в классическом смысле) задач ЛП:
![\begin{displaymath}\begin{array}{rcc}
L_p & \stackrel { \textstyle{\stackrel {{\...
...arrow } &
L^{\ast}\,. \\ [18pt]
& \mbox {Схема 3} &
\end{array}\end{displaymath}](img233.gif)
![]() означает переход к новой
задаче с наследованием (сохранением) оптимального множества.
Точная формулировка факта такова.
означает переход к новой
задаче с наследованием (сохранением) оптимального множества.
Точная формулировка факта такова.
![]() - задача из п. 9. Важным
является вопрос об аппроксимационном смысле задач P и
- задача из п. 9. Важным
является вопрос об аппроксимационном смысле задач P и ![]() по отношению к L и
по отношению к L и ![]() . Ниже этот смысл будет раскрыт
через термины лексикографической оптимизации.
. Ниже этот смысл будет раскрыт
через термины лексикографической оптимизации.
![]() разбиты на подсистемы
разбиты на подсистемы ![]()
![]() и
и
![]()
![]() , причем неравенства из одной подсистемы не ранжируются,
а сами подсистемы ранжируются, например, в соответствии с такими
упорядочениями:
, причем неравенства из одной подсистемы не ранжируются,
а сами подсистемы ранжируются, например, в соответствии с такими
упорядочениями:
![]() и
и
![]() .
Введенному упорядочению можно придать следующий смысл: ограничения
.
Введенному упорядочению можно придать следующий смысл: ограничения
![]() ,
, ![]() и
и
![]() ,
, ![]() носят директивный характер и предполагаются совместными,
остальные - факультативными (в целом же они могут быть
несовместными). Однако в силу введенной упорядоченности подсистем их
невязки
носят директивный характер и предполагаются совместными,
остальные - факультативными (в целом же они могут быть
несовместными). Однако в силу введенной упорядоченности подсистем их
невязки
![]()
![]() ,
,
![]()
![]() должно минимизировать последовательным образом в
соответствии с упорядочениями p и q. Как уже было
отмечено в предыдущем пункте, это эквивалентно постановке следующих
двух задач лексикографической оптимизации:
должно минимизировать последовательным образом в
соответствии с упорядочениями p и q. Как уже было
отмечено в предыдущем пункте, это эквивалентно постановке следующих
двух задач лексикографической оптимизации:
![\begin{displaymath}P_p(r):\ \max\nolimits_p \left\{ \left[
\begin{array}{c}-f_{m...
... \end{array}\right]\ \mbox{$\,\mid\,$}\ x \,\in\,M(r) \right\},\end{displaymath}](img245.gif)
![\begin{displaymath}P_q^\char93 (R):\ \min\nolimits_q \left\{ \left[
\begin{array...
...ay}\right]\ \mbox{$\,\mid\,$}\ u \,\in\,M^\char93 (R) \right\},\end{displaymath}](img246.gif)
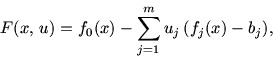
![\begin{displaymath}
\begin{array}{ccccc}
& \fbox{ I }& \stackrel {\textstyle\lon...
...equiv:\! C^{\ast}.\\ [36pt]
& & \mbox {Схема 4} & &
\end{array}\end{displaymath}](img279.gif)
![]() ,
,
![]() и
и
![]() таковы, что
таковы, что
![]() ,
то
,
то ![]() и
и ![]() называются оптимальными
стратегиями I-го и II-го игроков соответственно, а
называются оптимальными
стратегиями I-го и II-го игроков соответственно, а ![]() -
ценой игры. В нашей экономической интерпретации:
-
ценой игры. В нашей экономической интерпретации: ![]() - оптимальный план Производства,
- оптимальный план Производства, ![]() - вектор оптимальных
цен Рынка,
- вектор оптимальных
цен Рынка,
![]() - фактор равновесия
Производства и Рынка (
- фактор равновесия
Производства и Рынка (![]() - вектор равновесных цен).
- вектор равновесных цен).
![]() на основе принципа линеаризации
лежит следующая схема:
на основе принципа линеаризации
лежит следующая схема:
![]() означает линеаризацию всех
функций, формирующих задачу C, в точке p (в результате
получается задача ЛП: Lp),
означает линеаризацию всех
функций, формирующих задачу C, в точке p (в результате
получается задача ЛП: Lp),
![]() - это
операция автоматической замены p на
переменную x. Линеаризация в точке p произвольной
дифференцируемой функции f(x) состоит в замене ее линейной функцией
- это
операция автоматической замены p на
переменную x. Линеаризация в точке p произвольной
дифференцируемой функции f(x) состоит в замене ее линейной функцией
![]() .
.
![]() свойством взаимности не обладают,
поэтому в этом случае имеет смысл формулировать и обратную
теорему двойственности [6]:
свойством взаимности не обладают,
поэтому в этом случае имеет смысл формулировать и обратную
теорему двойственности [6]:
![[*]](crossref.gif) является соединением схем 2
и (14.1), о чем уже было сказано выше.
Схема не требует особых пояснений, так как все
необходимые разъяснения приведенных здесь символов имеются в
предыдущих пунктах. Если в качестве исходной задачи взять
является соединением схем 2
и (14.1), о чем уже было сказано выше.
Схема не требует особых пояснений, так как все
необходимые разъяснения приведенных здесь символов имеются в
предыдущих пунктах. Если в качестве исходной задачи взять
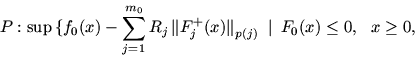
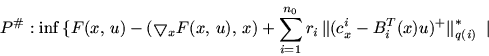
![]() ,
,
![]()
![]() ;
;
![\begin{displaymath}\bigtriangledown _x F(x) = \left[ \begin{array}{c}
\frac{\tex...
...ial x_n}
\end{array}\! \right]\! = [B_0(x),\,...\,,B_{n_0}(x)],\end{displaymath}](img311.gif)
![$c_x:=\ \bigtriangledown f_0(x) = \left[
\frac{\textstyle \partial f_0(x)}{\text...
...partial f_0 (x)}{\textstyle \partial x_n} \right]^T =
[c_x^1,\,...\,,c_x^{n_0}]$](img312.gif) .
.
![]() мы получим
задачу (16.5), обозначенную
мы получим
задачу (16.5), обозначенную
![]() . Последняя
является ничем иным как задачей, реализующей метод квадратичных
штрафных функций, примененным к задаче (16.3) со штрафной
константой
. Последняя
является ничем иным как задачей, реализующей метод квадратичных
штрафных функций, примененным к задаче (16.3) со штрафной
константой
![]() . Обозначим задачу (16.5) символом
. Обозначим задачу (16.5) символом
![]() . Нами показано
. Нами показано
![\begin{displaymath}\begin{array}{lcl}
L & \stackrel {\scriptstyle (*)} {\stackre...
...^*)_{{\,\mathrm{pen}}}.\\ [18pt]
& \mbox{Схема~6} &
\end{array}\end{displaymath}](img333.gif)
![\begin{displaymath}\begin{array}{lcl}
L & \stackrel {\scriptstyle (*)} {\stackre...
...^*)_{{\,\mathrm{reg}}},\\ [18pt]
& \mbox{Схема~7} &
\end{array}\end{displaymath}](img346.gif)
![]() ,
,
![]() .
.
![]() .
.
![]() чаще
записывают задачу:
чаще
записывают задачу:
![]() , где lj(x) - левые части системы
, где lj(x) - левые части системы
![]() , Rj > 0,
, Rj > 0,
![]() . В этом случае оценка 2) и
соотношение из следствия принимают вид:
. В этом случае оценка 2) и
соотношение из следствия принимают вид: