Next: 3 Свойства множества Up: НЕКОТОРЫЕ КОНЕЧНО-АДДИТИВНЫЕ ВЕРСИИ РАВНОМЕРНОГО Previous: 1 Постановка задачи
Пусть
![]() (
(![]() ) -- множество всех ограниченных
вещественнозначных к.-а. мер на
) -- множество всех ограниченных
вещественнозначных к.-а. мер на ![]() , а
, а
![]() (
(![]() ) -- множество
всех вероятностных мер на
) -- множество
всех вероятностных мер на ![]() . Оснащаем
. Оснащаем
![]() (
(![]() ) *-слабой
топологией
) *-слабой
топологией
![]() (
(![]() ). В данном конкретном случае пространство
). В данном конкретном случае пространство
![]() (
(![]() ) изометрически изоморфно пространству, топологически
сопряженному к пространству всех ограниченных в/з функций на
) изометрически изоморфно пространству, топологически
сопряженному к пространству всех ограниченных в/з функций на
![]() . Топологическое пространство
(
. Топологическое пространство
(![]() (
(![]() ),
),
![]() (
(![]() ))
--
))
-- ![]() -компакт, а множество
-компакт, а множество
![]() (
(![]() )
компактно в упомянутом ТП
(т.е. *-слабо компактно) в силу теоремы Алаоглу. Это означает, в
частности, возможность изотонного "прореживания" произвольной
направленности в
)
компактно в упомянутом ТП
(т.е. *-слабо компактно) в силу теоремы Алаоглу. Это означает, в
частности, возможность изотонного "прореживания" произвольной
направленности в
![]() (
(![]() ) до сходящейся поднаправленности. В
качестве исходной направленности можно, в частности, использовать
последовательность.
) до сходящейся поднаправленности. В
качестве исходной направленности можно, в частности, использовать
последовательность.
Если
t ![]()
![]() , обозначаем через
, обозначаем через ![]() меру Дирака, сосредоточенную в точке t (и определенную
на
меру Дирака, сосредоточенную в точке t (и определенную
на ![]() -алгебре
-алгебре ![]() всех подмножеств
всех подмножеств ![]() ). Кроме того,
полагаем
). Кроме того,
полагаем
![]() k
k ![]()
![]() , где
, где
![]()
![]() {1;2;...},:
{1;2;...},:
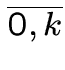 : ti(k)
: ti(k)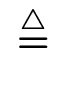
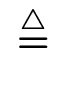 {ti(k) : i
{ti(k) : i 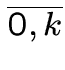 }.
}.
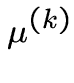
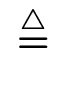
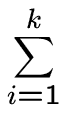
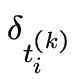 , k
, k 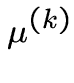 (
(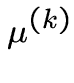 (Q) =
(Q) = 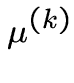 (Ik) = 1,
(Ik) = 1,
Устанавливается, что эта мера ![]() принадлежит множеству
принадлежит множеству ![]() всех к.-а. вероятностей на
всех к.-а. вероятностей на ![]() со свойствами
(
со свойствами
(![]() |
|![]() ) = l
и
) = l
и
![]() (Q) = 1 и является чисто к.-а. мерой в смысле разложения
Хьюитта-Иосида (то есть не имеет неотрицательных счетно-аддитивных
минорант, кроме тождественно равной нулю).
(Q) = 1 и является чисто к.-а. мерой в смысле разложения
Хьюитта-Иосида (то есть не имеет неотрицательных счетно-аддитивных
минорант, кроме тождественно равной нулю).