Bibliography

1

Korepin, V.E., Bogolyubov, N.M., and Izergin, A.G., Quantum Inverse Scattering Method and Correlation Functions, Cambridge Univ. Press, 1993.

2

Jing, N., Quantum Kac-Moody Algebras and Vertex Representations, Lett. Math. Phys., 1998, vol. 44, pp. 261-271.

3

Tarasov, V., Bilinear Identity for 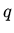$q$-Hypergeometric Integrals, Preprint. Osaka Univ., 1997; Osaka J. Math., 1999 (to appear).

4

Tarasov, V. and Varchenko, A., Geometry of 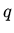$q$-Hypergeometric Functions, Quantum Affine Algebras and Elliptic Quantum Groups, Paris: Soc. Math. Fr., 1997, pp. 1-135 (Asterisque, vol. 246).

5

Tarasov, V. and Varchenko, A., Geometry of 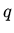$q$-Hypergeometric Functions as a Bridge between Yangians and Quantum Affine Algebras, Invent. Math., 1997, vol. 128, no. 3, pp. 501-588.

6

Nagel, B., The Discussion Concerning the Nobel Prize for Max Planck, Science Technology and Society in the Time of Alfred Nobel, New York: Pergamon, 1982.

7

Morse, F. and Feshbach, H., Methods of Theoretical Physics, New York: McGraw-Hill, 1953.

8

Courant, R. and Hilbert, D., Methoden der mathematischen Physik, Berlin: Springer, 1931.

9

Dirac, P., Quantized Singularities in the Electromagnetic Field, Proc. Roy. Soc. London A, 1931, vol. 133, pp. 60-72.

10

Yang, C.N., Selected Papers 1945-1980 with Commentary, San Francisco: Freeman, 1983.

11

Yang, C.N. and Mills, R., Conservation of Isotopic Spin and Isotopic Gauge Invariance, Phys. Rev., 1954, vol. 96, pp. 191-195.

12

Fock, V., L'equation d'onde de Dirac et la geometrie de Riemann, J. Phys. et Rad., 1929, vol. 70, pp. 392-405.

13

Weyl, H., Electron and Gravitation, Ztschr. Phys., 1929, vol. 56, pp. 330-352.

14

Klein, O., On the Theory of Charged Fields: Submitted to the Conf.: New Theories in Physics. Warsaw (Pol.), 1938, Surv. High Energy Phys., 1986, vol. 5, pp. 269.

15

Feynman, R.P., Quantum Theory of Gravitation, Acta Phys. Polon., 1963, vol. 24, pp. 697-722.

16

Lichnerowicz, A., Theorie globale des connexions et des groupes d'holonomie, Roma: Ed. Cremonese, 1955.

17

Faddeev, L. and Popov, V., Feynman Diagrams for the Yang-Mills Field, Phys. Lett. B, 1967, vol. 25, pp. 29-30.

18

Popov, V. and Faddeev, L., Perturbation Theory for Gauge-Invariant Fields, Preprint National Accelerator Laboratory, NAL-THY-57, 1972.

19

't Hooft, G., Renormalizable Lagrangians for Massive Yang-Mills Fields, Nucl. Phys. B, 1971, vol. 35, pp. 167-188.

20

Coleman, S., Secret Symmetries: An Introduction to Spontaneous Symmetry Breakdown and Gauge Fields: Lecture given at 1973 Intern. Summer School in Phys. Ettore Majorana. Erice (Sicily), 1973, Erice Subnucl. Phys., 1973.

21

't Hooft, G., When Was Asymptotic Freedom Discovered? Rehabilitation of Quantum Field Theory, Preprint, 1998, hep-th/9808154.

22

Gross, D., Twenty Years of Asymptotic Freedom, Preprint, 1998, hep-th/9809080.