В этом разделе рассмотрим
повторяющуюся 2![]() 2 игру (см., например, [8]-[11])
и, в частности, повторяющуюся ''дилемму заключенного'' (см.,
например, [12]-[13]). Для построения динамики мы
используем принцип неуменьшения выигрышей игроков, различные типы
поведения игроков и введенную в [7] специальную процедуру
сужения множества решений, основанную на нэшевских равновесиях во
вспомогательных биматричных играх.
2 игру (см., например, [8]-[11])
и, в частности, повторяющуюся ''дилемму заключенного'' (см.,
например, [12]-[13]). Для построения динамики мы
используем принцип неуменьшения выигрышей игроков, различные типы
поведения игроков и введенную в [7] специальную процедуру
сужения множества решений, основанную на нэшевских равновесиях во
вспомогательных биматричных играх.
Сначала рассмотрим биматричную 2![]() 2 игру
2 игру ![]() с матрицами
выигрыша 1-го и 2-го игроков соответственно
с матрицами
выигрыша 1-го и 2-го игроков соответственно
Предполагаем, что каждый игрок представляет большую группу
идентичных агентов или популяцию. Тогда смешанные стратегии могут
быть реализованы физически. В самом деле, если пара
![]() есть смешанная стратегия 1-го игрока, а
пара
есть смешанная стратегия 1-го игрока, а
пара
![]() - смешанная стратегия 2-го
игрока, то
- смешанная стратегия 2-го
игрока, то ![]() и
и ![]() могут быть интерпретированы как доли всех
тех агентов в первой и во второй группах соответственно, кто играет
первую чистую стратегию.
могут быть интерпретированы как доли всех
тех агентов в первой и во второй группах соответственно, кто играет
первую чистую стратегию.
Выигрыши 1-го и 2-го игроков определяются как
Пара ![]() в единичном квадрате
в единичном квадрате
Пусть теперь эта биматричная игра повторяется ![]() раз, где
раз, где ![]() -
бесконечное или большое число, неизвестное наперед. Пусть
-
бесконечное или большое число, неизвестное наперед. Пусть
![]() - начальное состояние. Предположим, что на
шаге
- начальное состояние. Предположим, что на
шаге
![]() игрокам разрешается перейти из
текущего состояния
игрокам разрешается перейти из
текущего состояния
![]() в любое состояние
в любое состояние
![]() , где
, где
Здесь ![]() - положительное, достаточно малое число. Малость
- положительное, достаточно малое число. Малость
![]() означает, что внутренняя структура групп
взаимодействующих агентов эволюционирует достаточно медленно.
означает, что внутренняя структура групп
взаимодействующих агентов эволюционирует достаточно медленно.
Будем реализовывать подход
![]() следуя принципу
неуменьшения выигрышей игроков. Существует много вариантов
такого перехода. Здесь мы применяем подход, основанный на
использовании нэшевских равновесий в вспомогательных биматричных
играх (см. [7,14,16]).
следуя принципу
неуменьшения выигрышей игроков. Существует много вариантов
такого перехода. Здесь мы применяем подход, основанный на
использовании нэшевских равновесий в вспомогательных биматричных
играх (см. [7,14,16]).
Пусть
![]() - текущее состояние в повторяющейся
биматричной игре. Сформулируем следующие задачи.
- текущее состояние в повторяющейся
биматричной игре. Сформулируем следующие задачи.
Теперь сконструируем вспомогательную биматричную игру
![]() с матрицами
с матрицами
![\begin{displaymath}A^{\ast}=\left(
\begin{array}[c]{cc}
f_{1}(p^{1},q^{1}) & f_{...
...ex]
f_{2}(p^{2},q^{1}) & f_{2}(p^{2},q^{2})
\end{array}\right) \end{displaymath}](img286.gif)
В этой игре ![]() -тая стратегия 1-го игрока есть ``выбрать
-тая стратегия 1-го игрока есть ``выбрать
![]() '', а
'', а ![]() -тая стратегия 2-го игрока есть ``выбрать
-тая стратегия 2-го игрока есть ``выбрать
![]() ''
''
![]() . Чтобы достичь
. Чтобы достичь
![]()
![]() , игроки находят нэшевские
равновесия. Легко показывается, что эта биматричная игра имеет по
крайней мере одно нэшевское равновесие в классе чистых стратегий.
Возможны два случая.
, игроки находят нэшевские
равновесия. Легко показывается, что эта биматричная игра имеет по
крайней мере одно нэшевское равновесие в классе чистых стратегий.
Возможны два случая.
1. Игра имеет единственное нэшевское равновесие
![]() .
Тогда мы принимаем
.
Тогда мы принимаем
![]() .
.
2. Игра имеет два нэшевских равновесия
![]() и
и
![]() . Тогда в качестве
. Тогда в качестве
![]() берем либо
берем либо
![]() либо
либо
![]() с равной частотой.
с равной частотой.
Итак, динамика повторяющейся биматричной 2![]() 2 игры
определена полностью.
2 игры
определена полностью.
Теперь переходим к повторяющейся ''дилемме заключенного''. В этой игре матрица выигрышей игроков суть
![\begin{displaymath}
A=\left(
\begin{array}[c]{cc}
a_{11} & a_{12}\\
a_{21} & a...
...[c]{cc}
a_{11} & a_{21}\\
a_{12} & a_{22}
\end{array}\right), \end{displaymath}](img297.gif)
Естественно рассмотреть задачу: как следует выбрать типы поведений
игроков, чтобы привести начальное состояние
![]() в
состояние кооперации
в
состояние кооперации
![]() , используя описанную выше
динамику.
, используя описанную выше
динамику.
Множество начальных состояний
![]() , решающих задачу
5.3, обозначим через
, решающих задачу
5.3, обозначим через ![]() .
.
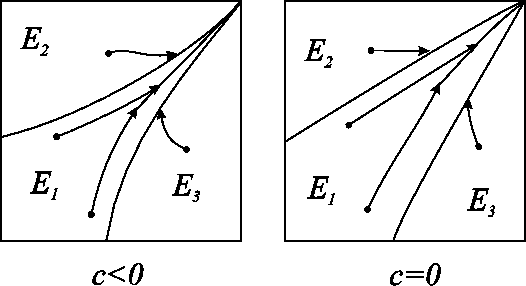
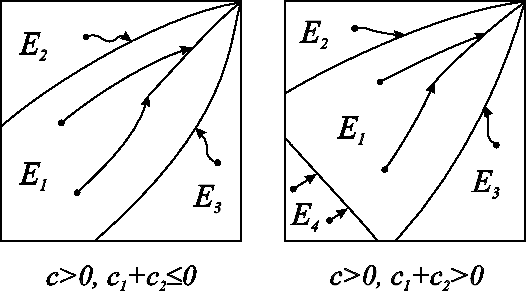
Множество ![]() изображено на рис. 2-5 для разных случаев.
изображено на рис. 2-5 для разных случаев.
Обозначим через ![]() (
(![]() ) множество начальных состояний,
решающих задачу 5.4, используя нормальный тип поведения для 1-го
игрока (2-го игрока) и альтруистический тип поведения для 2-го
игрока (1-го игрока).
) множество начальных состояний,
решающих задачу 5.4, используя нормальный тип поведения для 1-го
игрока (2-го игрока) и альтруистический тип поведения для 2-го
игрока (1-го игрока).
Множества ![]() и
и ![]() изображены на рис. 2-5.
изображены на рис. 2-5.
Заметим, что только для случая ![]() ,
,
![]() имеем
имеем
![]() . Обозначим
. Обозначим
![]() (см. рис. 5).
(см. рис. 5).
Поступила 16.07.2000