Проблема исследования поведения ОД [1]-[3] и пучков траекторий управляемых систем при возмущении различных ограничений (на управление) имеет самостоятельное значение, а также важна с точки зрения обоснованного анализа экстремумов критериев и их реализуемости в условиях использования неточных моделей. Мы ограничимся вопросом о влиянии на результат ослабления системы условий, имея целью исследование проблем корректных расширений, направленных на извлечение определенных полезных эффектов, сопутствующих нередко процессу замены точных ограничений приближенными ( см., например, [4, гл. III, IV]). Конструкции расширений, подобные [4], но относящиеся к задачам управления с интегральными ограничениями (и, в частности, с ограничением на ресурс), рассматривались в [5], где в качестве обобщенных управлений были использованы функции ограниченной вариации. В [6]-[10] и в ряде других работ построены конструкции обобщенных задач о достижимости элементов ТП, реализуемые в классах конечно-аддитивных (к.-а.) мер; последние использовались в качестве обобщенных элементов (ОЭ). В классе таких ОЭ (к.-а. мер) в [6]-[10] конструируются множества допустимых элементов (МДЭ), характеризующие асимптотику реализуемых аналогов ОД при ослаблении комплекса интегральных ограничений и допускающие идейные аналогии с построениями [4] для задач управления с геометрическими ограничениями. Была обозначена, для асимптотических конструкций [4] и [6]-[8], проблема (см. также [9]-[10]), связанная с использованием моделей в классе подходящих ТП и соответствующих типов непрерывных преобразований этих ТП (см. [6, гл. 2], [7, гл. 3,5], [10]). В настоящей работе мы продолжаем исследование этой общей проблемы топологическими средствами.
Подробное обсуждение содержательных задач, приводящих к использованию расширений и, в частности, моделей с применением (в качестве ОЭ) к.-а. мер имеется в [11]. Конструкции [11] являются, по сути дела, конкретизацией общих положений настоящей работы, ориентированных на широкий круг задач управления с ограничениями различных типов. По этой причине в данном изложении (по соображениям объема) опущено рассмотрение мотивирующих примеров, которые заинтересованный читатель без труда найдет в [11] и в монографиях [6,7]. Мы ставим здесь своей целью анализ общих закономерностей, связанных с проблематикой корректных расширений, интерпретируя построения [11], как весьма важный частный случай. Другой частный случай можно получить на основе соответствующего развития подхода [4], где в качестве ОЭ используются либо мерозначные функции, либо, в редакции, отвечающей конструкциям "стратегических" мер, - регулярные борелевские меры (РБМ) на декартовом произведении пространств, одно из которых - временной интервал; при этом требуется маргинальное согласование упомянутых РБМ с мерой Лебега. В этой связи, наряду с [4], см., например, [12,13] и, для игровых версий данной конструкции расширения, - монографии [14]-[16], а также многие другие работы (см. библиографию [4]).
Отметим, что элементы теории расширений использовались Н.Н.Красовским в фундаментальном понятии стабильного множества для нелинейной дифференциальной игры; с применением этого понятия Н.Н.Красовский и А.И.Субботин установили основополагающую теорему об альтернативе (см. [2,14]), которая определила факт существования решения и структуру дифференциальной игры общего вида. Следует отметить в этой связи принципиальный результат А.И.Субботина о существенности класса разрывных позиционных стратегий в вопросах достижения значения игры. В свою очередь, использование таких стратегий потребовало построения конструктивных движений [2,14] конфликтно-управляемой системы, получаемых в форме равномерных пределов пошаговых движений (ломаных Эйлера), т.е. применения конструкции, которую также можно интерпретировать, как расширение, поскольку представление конструктивных движений в виде решений управляемого дифференциального уравнения возможно, вообще говоря, лишь при расширении последнего с использованием мер, либо аппарата дифференциальных включений.
Можно отметить и некоторые версии расширений с
использованием ультрафильтров измеримых пространств или, что то же
самое, двузначных к.-а. вероятностей (см., например, [17,18]);
эти расширения близки в идейном отношении типичным
конструкциям компактификаций, используемым в общей топологии (см. в
этой связи [19]-[23]; в частности, см.
[22, стр. 271-274]), хотя имеются и особенности, определяемые
связями в виде представлений заданных отображений посредством
"непрерывных"
суперпозиций (см. следующий раздел). Все эти обстоятельства требуют,
как представляется, некоторого достаточно универсального подхода, в
основе которого лежат топологические конструкции расширений, не
обязательно сводящихся к компактификациям (о задачах такого рода см. в
[7], [9]-[11])
и определяемые совсем "небольшим" набором свойств. Цели и
задачи таких построений находятся, по видимому, за пределами самой
топологии; их можно, однако, рассматривать в контексте весьма
актуальных ее приложений, поскольку отсутствие у многих
экстремальных задач свойства устойчивости в обычном ее понимании и,
вместе с тем, наличие некоторых аналогов этого свойства
(в форме асимптотической
нечувствительности при возмущении части ограничений) делает достаточно
важной уже проблему классификации возможных случаев с точки зрения
последствий использования неточных моделей для
прикладных задач. Топологическое оснащение требуется, по существу, в
задачах импульсного управления, где элементы конструкции расширения
``не укладываются", как правило, в рамки представлений, характерных для
метризуемых ТП. Таким образом, представляется целесообразным
исследование характерных (для конструкций расширений) топологических
методов, ориентированных на использование идеализированных (и,
следовательно,
более "совершенных") пространств ОЭ. Следует отметить, что
материализация упомянутых ОЭ традиционно осуществлялась в
пространствах мер (РБМ, либо к.-а. мер) при оснащении этих пространств
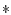-слабой топологией. Разумеется, последнее обстоятельство
предполагало фактическое отождествление ОЭ с линейными непрерывными
функционалами на соответствующих банаховых пространствах. Упомянутая
топология, определяющая основу расширения пространства решений,
естественно интерпретируется в терминах тихоновского произведения ТП.
Последнее целесообразно использовать и в других целях, в том числе
(см. [6,7]) при формализации допустимых процедур
ослабления системы ограничений (в частности, интегральных
ограничений). В этой связи полезно отметить, что в конструкциях
расширения задач управления с геометрическими ограничениями,
систематическое изучение которых было начато Л.С.Понтрягиным, удается
использовать метризуемые "компактификаторы" (см.
[4, гл. III,IV]). Однако, по всей видимости, эту возможность
следует рассматривать скорее как исключение.