игрок может выбирать число
Рассмотрим сейчас случай, когда
отображению (2.1) позволяется быть
разрывным. Чтобы обеспечить ненулевой
результат, соответствующий
игрок может
выбирать число ![]() следующим
образом:
следующим
образом:
Имеем
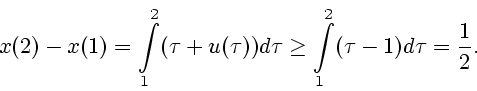
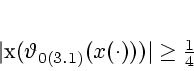
Другое правило для выбора числа ![]() может быть дано формулой
может быть дано формулой
С другой стороны, каким бы ни было
отображение (2.1), нельзя обеспечить
более хороший результат для игрока,
выбирающего ![]() , потому что для
программного управления
, потому что для
программного управления
Отметим, что как (3.1), так и (3.3)
являются разрывными отображениями в
смысле (2.1). Оба они удовлетворяют
условию (NA).
Отметим также, что в рассматриваемой
задаче управления число (3.3)
удовлетворяет неравенству
![]() .
Действительно, если
.
Действительно, если
![]() , то
, то
![]() , из неравенства (3.2)
вытекает
, из неравенства (3.2)
вытекает ![]() и, следовательно,
и, следовательно,
![]() , что
противоречит предположению
, что
противоречит предположению
![]() .
.
Однако можно выбрать решения ![]() задачи
управления, для которых числа
задачи
управления, для которых числа
![]() сколь угодно
близки к
сколь угодно
близки к ![]() . Это можно показать
модификацией функций (3.4), (3.5).
Возьмем
. Это можно показать
модификацией функций (3.4), (3.5).
Возьмем
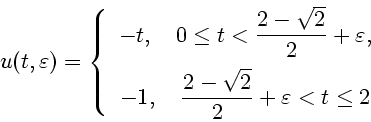
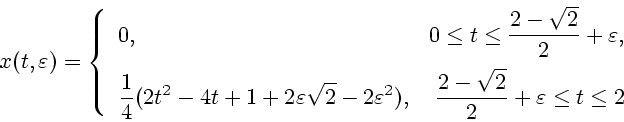
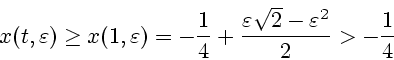
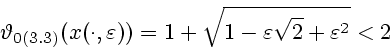
Интересно сравнить правила (3.1) и
(3.3) как два различных способа
поведения соответствующего игрока. В
случае (3.1) в момент времени ![]() игроку становится известна величина
игроку становится известна величина ![]() ,
и на основе этой информации принимается
решение либо остановить игру немедленно,
либо дождаться ее окончания при
,
и на основе этой информации принимается
решение либо остановить игру немедленно,
либо дождаться ее окончания при ![]() .
(Очевидно, любое невырожденное правило
этого типа описывается разрывным
отображением.) Правило (3.1) требует
измерения фазового состояния
.
(Очевидно, любое невырожденное правило
этого типа описывается разрывным
отображением.) Правило (3.1) требует
измерения фазового состояния ![]() только в
одной точке
только в
одной точке ![]() , в то время как
отображение (3.3) требует измерять
, в то время как
отображение (3.3) требует измерять
![]() непрерывно на отрезке
непрерывно на отрезке ![]() . Момент
времени
. Момент
времени ![]() , подсчитанный в
соответствии с формулой (3.3),
меньше или равен моменту, заданному
формулой (3.1). По определению, для
фиксированной траектории момент
времени, задаваемый (3.3), является
наименьшим возможным из тех, что
достигают результат
, подсчитанный в
соответствии с формулой (3.3),
меньше или равен моменту, заданному
формулой (3.1). По определению, для
фиксированной траектории момент
времени, задаваемый (3.3), является
наименьшим возможным из тех, что
достигают результат ![]() . Как было
показано выше, в рассматриваемой задаче
этот момент времени всегда строго меньше,
чем
. Как было
показано выше, в рассматриваемой задаче
этот момент времени всегда строго меньше,
чем ![]() , хотя он может быть произвольно
близок к
, хотя он может быть произвольно
близок к ![]() . Правило (3.3) всегда дает
гарантированный результат
. Правило (3.3) всегда дает
гарантированный результат ![]() , в то
время как правило (3.1) может
доставить более хороший результат для
игрока, выбирающего
, в то
время как правило (3.1) может
доставить более хороший результат для
игрока, выбирающего ![]() в случае,
если противник совершает ошибки. Можно
также указать другие разумные способы
назначения момента времени
в случае,
если противник совершает ошибки. Можно
также указать другие разумные способы
назначения момента времени ![]() ,
которые доставляют гарантированный
результат.
,
которые доставляют гарантированный
результат.
Поступила 30.07.99