4. Оценки многозначных состояний: функция Минковского

Рассмотрим специальный класс билинейных динамических систем вида (3.1), где при каждом $t$ значениями ${\cal A}(t)$ многозначной функции ${\cal A}$ являются множества всех диагональных $n\times n$ матриц $A(t)$ с неизвестными, но ограниченными диагональными элементами $a_{ii}(t)$:

$${\cal A}(t)=\{A(t): a_{ij}=0 \mbox{ для } i\not=j, \ a_i=a_{ii}, \ a=(a_1, \dots , a_n) \in A_0\}.$$

Здесь $A_0 \in \mathrm{St} ({\Bbb R}^n)$. Предположим, как и ранее, что начальное множество $X_0$ лежит в пространстве $\mathrm{St} ({\Bbb R}^n)$.

Рассмотрим задачу построения аппроксимации первого порядка для многозначной функции $X[t]$ на основе эволюционного уравнения (3.2), при этом положим $Y(t)={\Bbb R}^n$ (фазовые ограничения отсутствуют). Отметим, что возможные вычислительные процедуры, основанные на использовании данного уравнения и ориентированные на точное или приближенное построение искомых многозначных состояний $X[t]$, имеют итерационный характер и близки известному методу Эйлера численного решения дифференциальных уравнений. Поэтому представляется важным иметь эффективные алгоритмы обработки каждого шага итерации. Данная задача и решается здесь для множеств ограничений достаточно простой структуры.

Итак, рассмотрим первый шаг аппроксимации первого порядка (для достаточно малых моментов $\sigma$). Тогда из теоремы 3.2 имеем ( $t=t_0 + \sigma$)

$$h\left(X[t],((I+ \sigma {\cal A}_0)\ast X_0+\sigma P)\right)... ..., \ \ \ \ \lim\limits_{\sigma \to +0}\sigma ^{-1}o(\sigma) =0,$$

где ${\cal A}_0={\cal A}(t_0)$ и $P=P(t_0)$.

Для каждого множества $M \in\mathrm{St}({\Bbb R}^n)$ символом $h_M(z)$ будем обозначать функцию Минковского ( $z \in {\Bbb R}^n$):

$$h_M(z)=\inf \{t>0 : z \in t M \}.$$

Наша основная цель состоит в том, чтобы вычислить функцию Минковского для множества $X[t]$ или для его аппроксимации $((I+ \sigma {\cal A}_0)\ast X_0+\sigma P)$, но мы разобьем решение на два более простых этапа, позволяющих построить оценку сверху по включению для указанной аппроксимации.

Вначале найдем функцию Минковского для множества ${\cal A}_0\ast X_0$ и затем получим формулу для вычисления функции Минковского для алгебраической суммы множеств.

Отметим следующие общие свойства функций Минковского.

Лемма 4.1   Пусть $M \in\mathrm{St}({\Bbb R}^n)$ и для некоторого $\epsilon >0$ $\epsilon S \subset M$. Тогда функция $h_M(z)$ является положительно однородной и $h_M(0)=0$.

Будем считать в дальнейшем, что выполнено предположение 3.1.

Пусть символ $\rho (l\vert C)$ означает опорную функцию выпуклого компактного множества $C \in \mbox{Conv\,} {\Bbb R}^n$, вычисленную на элементе $l \in {\Bbb R}^n$,

$$\rho (l\vert C)=\max \{(l,c) :\ c \in C\}$$

(здесь $(l,c)=l'c$ означает скалярное произведение в ${\Bbb R}^n$).

Непосредственно из определения функции Минковского и с учетом предположения 3.1 нетрудно получить следующий результат.

Лемма 4.2   Для любого $z \in {\Bbb R}^n$ такого, что $z_i \not= 0$ ( $i=1, \dots ,n)$, справедлива формула

$$h_{{\cal A}_0 \ast X_0} (z)=$$

$$=\min \left\{\max\limits_{l\not= 0}\frac{\sum\limits_{i=1}^{... ...t X_0)} :\ a\in A_0,\ a_i\not= 0 \ (i=1, \dots ,n)\ \right\} .$$ (4.1)

Пример 4.1   Предположим, в частности, что множества $A_0$, $X_0$ имеют следующий простой вид:

$$A_0 = \left\{a\in {\Bbb R}^n : \sum\limits_{i=1}^{n}\vert a_i\vert^2\leq 1 \right\},$$

$$X_0 = \left\{x\in {\Bbb R}^n : \sum\limits_{i=1}^{n}\vert x_i\vert^2\leq 1 \right\},$$

т.е. являются единичными шарами в евклидовом пространстве ${\Bbb R}^n$.

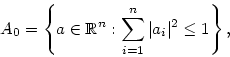
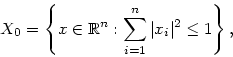
Тогда вычисления по формуле (4.1) (с использованием техники множителей Лагранжа) приводят к результату:

$$h_{{\cal A}_0 \ast X_0} (z)= \sum\limits_{i=1}^{n}\vert z_i\vert,$$ (4.2)

причем в силу леммы 4.1 формула (4.2) остается справедливой при всех $z \in {\Bbb R}^n$, и следовательно,

$${\cal A}_0 \ast X_0 = \left\{z \in {\Bbb R}^n : \sum\limits_{i=1}^{n}\vert z_i\vert \leq 1 \right\}.$$ (4.3)

Имеет место и более общий результат.

Теорема 4.1   Пусть

$$A_0 = \left\{a\in {\Bbb R}^n : \sum\limits_{i=1}^{n}\vert a_i\vert^p\leq 1 \right\},$$

$$X_0 = \left\{x\in {\Bbb R}^n : \sum\limits_{i=1}^{n}\vert x_i\vert^q\leq 1 \right\}.$$

($p,q>0$). Тогда

$$h_{{\cal A}_0\ast X_0}(z)= \left(\frac{q}{p}\right)^{\frac{... ...ert z_i\vert^r\right)^{\frac{1}{r}}, \ \ \ \ r=\frac{pq}{p+q}.$$

Д о к а з а т е л ь с т в о. Указанные в теореме формулы получаются прямым вычислением в результате вспомогательной замены $b_i=\vert a_i\vert^{p/2}$, $y_i=\vert x_i\vert^{q/2}$ и из равенства (4.2).

Пример 4.2   Рассмотрим случай $p=q=1$. Тогда из теоремы 4.1 сразу же получаем

$${\cal A}_0\ast X_0= S_{\frac{1}{2}} =\left\{z: \sum\limits_{i=1}^{n} \vert z_i\vert^{\frac{1}{2}} \leq 1 \right\}.$$

Таким образом, множество ${\cal A}_0\ast X_0$ уже теряет свойство выпуклости, оставаясь звездным. Причем отсутствие выпуклости произведения может наблюдаться и при равномерно выпуклых исходных множествах, при $p, q>1$, если только $(p^{-1} + q^{-1}) > 1$.

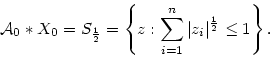
Верхняя по включению оценка шага аппроксимации $X[t]$ следует из соотношения:

$$X[t]\subset (X_0+ \sigma {\cal A}_0\ast X_0+\sigma P) + o(\sigma)S$$

и из "конволюционной" формулы для вычисления функции Минковского алгебраической суммы звездных множеств, приведенной в следующей теореме.

Теорема 4.2   Пусть $A,B$ - некоторые множества из $St({\Bbb R}^n)$, причем для некоторого $\epsilon >0$ $\epsilon S \subset A\cap B$. Тогда

$$h_{A+B}= \min_{z_*}\max_{0\leq \alpha \leq 1} \{\alpha h_A (z_*) + (1-\alpha)h_B (z-z_*)\}.$$ (4.4)

Д о к а з а т е л ь с т в о. Отметим, что из предположений теоремы вытекает достижимость минимума в формуле (4.4). Зафиксируем произвольный вектор $z \in {\Bbb R}^n$ и положим

$$T= \min_{z_*}\max_{0\leq \alpha \leq 1} \{\alpha h_A (z_*) + (1-\alpha)h_B (z-z_*)\}=$$

$$=\min_{z_*}\max \{h_A (z_*), h_B (z-z_*)\}.$$

Тогда существует $z_*$ такой, что одновременно выполняются два неравенства: $T\geq h_A(z_*)$ и $T\geq h_B(z-z_*)$. Отсюда получаем

$$z_* \in TA, \ \ \ \ \ (z-z_*) \in TB.$$

Но тогда $z=z_* + (z-z_*) \in T(A+B)$ и, следовательно, $h_{A+B}(z) \leq T$.

Обратно, пусть для некоторого числа $t>0$ выполнено включение $z \in t(A+B)$. Тогда $t^{-1}z\in (A+B)$ и найдутся элементы $z_1 \in A$, $z_2\in B$ такие, что $t^{-1}z=z_1 +z_2$, причем $h_A(z_1)\leq 1$, $h_B(z_2) \leq 1$. Обозначим $z_*=tz_1$ (а тогда $tz_2=z-z_*$) и получим снова два неравенства

$$h_A(z_*)\leq 1, \ \ \ \ \ h_B(z-z_*) \leq 1,$$

которые должны быть выполнены одновременно. Поэтому

$$\max \{h_A(z_*),h_B(z-z_*)\} \leq t,$$

откуда получаем

$$\min_{z_*}\max \{h_A (z_*), h_B (z-z_*)\} \leq t.$$

Но тогда и для точной нижней грани $h_{A+B}(z)$ чисел $t$ выполнено аналогичное неравенство, что и требовалось доказать.

Приведем еще один вариант теоремы 4.1 для эллипсоидальных множеств ограничений $A_0$, $X_0$.

Теорема 4.3   Пусть

$$A_0 = \{a\in {\Bbb R}^n : (a,Ma)\leq 1\},$$

$$X_0 = \{x\in {\Bbb R}^n : (x,Nx)\leq 1\},$$

где $M$, $N$ симметричные положительно определенные матрицы. Тогда имеет место формула

$$h_{{\cal A}_0\ast X_0}(z)= \vert\vert N^{-\frac{1}{2}}M^{-\frac{1}{2}}z\vert\vert _{ l_1},$$

что эквивалентно соотношению

$${\cal A}_0\ast X_0=N^{\frac{1}{2}}M^{\frac{1}{2}}S_1,$$

где $S_1$ единичный шар (с центром в $0$) в ${\Bbb R}^n$ относительно ${l}_1$-нормы.

Доказательство аналогично доказательству теоремы 4.1.

Пример 4.3   Пусть $n=2$ и множества $A_0$, $X_0$ имеют вид:

$$A_0 = \{a\in {\Bbb R}^2 : \vert a_1\vert+\vert a_2\vert\leq 1\},$$

$$X_0 = \{x\in {\Bbb R}^2 : \vert x_1\vert +\vert x_2\vert\leq 1\}.$$

Тогда

$${\cal A}_0 \ast X_0 = \{z \in {\Bbb R}^2 : \sqrt{\vert z_1\vert}+\sqrt{\vert z_2\vert} \leq 1\}.$$

Вычислив функцию Минковского суммы множеств $X_0 + {\cal A}_0\ast X_0$, получим равенство

$$X_0 + {\cal A}_0\ast X_0 = 2X_0 =2S_1,$$

причем при значениях $0 < \sigma \leq 1$ верна подобная формула

$$X_0 + \sigma {\cal A}_0\ast X_0 = (1+\sigma )X_0 = (1+\sigma)S_1.$$

При $\sigma >1$ нетрудно показать, что свойство выпуклости теряется. Аналогично, не будет выпуклым и множество $(I+\sigma {\cal A}_0)\ast X_0$. Действительно, точки $z_*=(1 +\sigma ,0)$ и $z_{**}=(0, 1+\sigma)$ принадлежат всем трем множествам, связанным цепочкой включений

$$(I+\sigma {\cal A}_0)\ast X_0 \subset (X_0 + \sigma {\cal A}_0\ast X_0) \subset (1+\sigma)S_1,$$

однако выпуклая комбинация $(z_* +z_{**})/2$ лежит лишь в последнем из них. Заметим, что для пространства размерности $n>2$ множество $S_1 +A_1 \ast S_1$ отлично от $2S_1$ и более того, невыпукло и звездно.

Отметим в заключение, что полученные оценки могут быть использованы при построении итерационных процедур при компьютерном моделировании на основе дискретных версий эволюционных уравнений типа уравнений интегральной воронки. Хотя предлагаемые множества дают оценки сверху аппроксимаций траекторных трубок, однако даже при помощи таких "грубых" операций удается проанализировать нелинейные эффекты, такие как отсутствие выпуклости множеств достижимости неопределенных систем, и тем не менее приближенно описать границы указанных множеств.

Отметим, наконец, что использование внешних аппроксимаций многозначных функций $X[t]$ позволяет связать данный подход с техникой исчисления многозначных оценок, построенных на основе эллипсоидов или многогранников ([15,16,20]).

Поступила 27.06.2000