О p-РЕГУЛЯРНЫХ ГРУППАХ
А. А. Финогенов
Аннотация:
Приводится
простое доказательство регулярности конечных p-групп класса
нильпотентности меньше p,
не использующее собирательный процесс Холла,
и обобщаются некоторые результаты Гровза о многообразиях,
минимальных среди содержащих не регулярные p-группы.
Регулярные p-группы были введены в рассмотрение Ф.Холлом [6]
в 1933 году и активно исследовались многими авторами.
Основным результатом, стимулировавшим их изучение, была так называемая
собирательная формула Холла. Ее
доказательства, несмотря на значительные улучшения
([1], [8]) остаются
довольно трудными, так как основаны на
применении собирательного процесса.
В данной статье приводится
простое доказательство собирательной формулы Ф.Холла,
не использующее собирательный процесс,
и обобщаются некоторые результаты Гровза [5].
Мы будем использовать стандартные обозначения
[1]. Кроме того, положим
(x, y) = y-px-p(xy)p.
Будем
называть группу p-регулярной (везде далее p -- простое
число, не равное 2),
если
для любых x, y 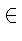 G
G
и p-абелевой, если (x, y)=1.
Регулярные p-группы в смысле Ф. Холла --
это в точности
конечные p-регулярные
p-группы.
Интересно, что многие
утверждения о
конечных регулярных p-группах легко переносятся на
p-регулярные нильпотентные группы [4].
Для этого достаточно заменить в
доказательствах индукцию по порядку группы на индукцию по
классу нильпотентности.
Лемма 1.
Если G -- группа с тождеством
(x[y, z])p = xp, x,
y 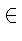 G, c
G, c 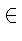 G' и s -- целое,
то
G' и s -- целое,
то
- 1.
-
(xc)p = xp;
- 2.
-
exp (G') = p,
Gp
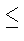 Z(G); [2]
Z(G); [2]
- 3.
-
(xs, ys) = (x, y)s.
Д о к а з а т е л ь с т в о.
(1) Пусть c можно представить в виде
произведения
n
коммутаторов. Тогда
(xc)p = (xd[a, b])p = (xd )p, где d представим
уже в виде произведения n - 1 коммутатора, и очевидная индукция показывает,
что
(xc)p = xp.
(2) Взяв x = 1, из (1) получим
exp (G') = p.
Из равенства
(xp)y = (xy)p = (x[x, y])p = xp следует
Gp 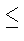 Z(G).
Z(G).
(3) С одной стороны
(xsys)p = xpsyps(xs, ys), но
с другой стороны для некоторого c 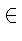 G'
(xsys)p = ((xy)sc)p = (xy)ps = (xpyp(x, y))s = xpsyps(x, y)s.
И после приравнивания и сокращений получим требуемое.
G'
(xsys)p = ((xy)sc)p = (xy)ps = (xpyp(x, y))s = xpsyps(x, y)s.
И после приравнивания и сокращений получим требуемое.
Предложение 1.
Для нильпотентной группы G следующие утверждения эквивалентны:
- 1.
- G p-регулярна.
- 2.
- Любая 2-порожденная секция
(секцией будем называть факторгруппу подгруппы) группы G,
удовлетворяющая тождеству
(x[y, z])p = xp, p-абелева.
Д о к а з а т е л ь с т в о.
1 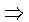 2.
Ясно, что любая секция p-регулярной группы сама p-регулярна, а ее
p-абелевость следует из (2) леммы 1.
2.
Ясно, что любая секция p-регулярной группы сама p-регулярна, а ее
p-абелевость следует из (2) леммы 1.
2 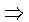 1.
Воспользуемся индукцией по классу нильпотентности. Пусть a, b
1.
Воспользуемся индукцией по классу нильпотентности. Пусть a, b 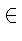 G,
H =
G,
H = 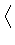 a, b
a, b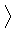 /(
/(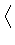 a, b
a, b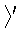 )p;
x, y, z
)p;
x, y, z 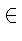 H и
P =
H и
P = 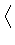 x,[y, z]
x,[y, z]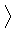 .
Заметим, что
cl (P) < cl (H)
.
Заметим, что
cl (P) < cl (H) 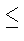 cl (G), а так как любая
секция p является также и секцией G, по предположению индукции
p p-регулярна, а значит, и p-абелева.
Следовательно,
(x[y, z])p = xp[y, z]p = xp, и по условию H p-абелева.
Отсюда
a-pb-p(ab)p
cl (G), а так как любая
секция p является также и секцией G, по предположению индукции
p p-регулярна, а значит, и p-абелева.
Следовательно,
(x[y, z])p = xp[y, z]p = xp, и по условию H p-абелева.
Отсюда
a-pb-p(ab)p 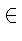 (
(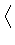 a, b
a, b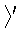 )p.
)p.
Определение 1.
Будем называть многообразие
минимальным не
p-регулярным1,
если оно содержит не p-регулярную группу, но все его собственные
подмногообразия состоят из p-регулярных групп.
Пусть
P -- свободная группа
нильпотентного минимального не p-регулярного
многообразия групп со свободным
базисом {a, b} и cl (P) = n. Ясно, что P не p-регулярная
и, значит,
порождает
все многообразие. Из предложения 1 следует,
что на p выполнено
тождество
(x[y, z])p = xp, и по (2) леммы 1
exp(P') = p.
Определим коммутаторные слова ui(a, b),
(i = 1,..., p - 1)
следующим образом:
поскольку
P/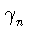 (P) p-абелева (так как она лежит в
собственном подмногообразии), то
(a, b)
(P) p-абелева (так как она лежит в
собственном подмногообразии), то
(a, b) 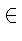
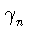 (P),
и, значит, на P выполнено
(P),
и, значит, на P выполнено
(
a,
b) =
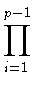 ui
ui(
a,
b), (*)
Предложение 2.
Пусть P -- свободная группа нильпотентного минимального не
p-регулярного многообразия со свободным
базисом {a, b}, и cl (P) = n.
Тогда
n = 1 + k(p - 1) и k 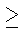 1.
1.
Д о к а з а т е л ь с т в о.
Так как {a, b} -- свободный базис и ui(a, b)
состоит из коммутаторов веса n, по [1, 3.6.8],
для любого целого s
(
as,
bs) =
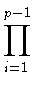 ui
ui(
as,
bs) =
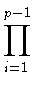 ui
ui(
a,
b)
sn = (
a,
b)
sn.
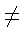 1,
по (2) леммы 1 |(a, b)| = p.
Итак,
s
1,
по (2) леммы 1 |(a, b)| = p.
Итак,
s 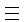 snmod p для любого s.
Отсюда следует, что
n = 1 + k(p - 1). Очевидно, k
snmod p для любого s.
Отсюда следует, что
n = 1 + k(p - 1). Очевидно, k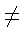 0.
0.  Если в многообразии есть не p-регулярная группа,
то стандартные рассуждения показывают, что это многообразие
содержит минимальное не p-регулярное подмногообразие.
А так как по предложению 1 многообразие групп класса p - 1 не может
содержать минимального не p-регулярного подмногообразия,
мы получаем утверждение, эквивалентное собирательной формуле Ф.Холла:
Если в многообразии есть не p-регулярная группа,
то стандартные рассуждения показывают, что это многообразие
содержит минимальное не p-регулярное подмногообразие.
А так как по предложению 1 многообразие групп класса p - 1 не может
содержать минимального не p-регулярного подмногообразия,
мы получаем утверждение, эквивалентное собирательной формуле Ф.Холла:
Следствие 1. (Ф.Холл)
Группы класса нильпотентности p - 1 p-регулярны.
Нашей следующей целью будет доказательство двух утверждений:
Теорема 1.
Пусть в каждой группе G из нильпотентного многообразия
для всех целых s и m
(0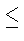 s < m) и элементов x, y из G выполнено:
s < m) и элементов x, y из G выполнено:
[
c1,...,
cn]
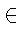
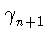
(
G)
. (
G')
p,
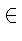 {x, y};
n = 1 + (s + m)(p - 1)
и в последовательности
c1,..., cnx встречается
1 + s(p - 1) раз, а y -- m(p - 1) раз.
Тогда любая группа из этого многообразия
p-регулярна.
{x, y};
n = 1 + (s + m)(p - 1)
и в последовательности
c1,..., cnx встречается
1 + s(p - 1) раз, а y -- m(p - 1) раз.
Тогда любая группа из этого многообразия
p-регулярна.
Следствие 2.(Гровз [5])Многообразие групп
класса не более
3(p - 1) состоит из p-регулярных групп тогда и только тогда,
когда в каждой группе G из
этого многообразия для любых x, y 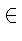 G выполнено
условие:
Нам потребуется
G выполнено
условие:
Нам потребуется
Лемма 2.
Пусть G -- группа с тождеством
(x[y, z])p = xp. Тогда для любых элементов
x, y, z 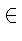 G и целых чисел s и t выполнено:
G и целых чисел s и t выполнено:
- 1.
-
(x, y) = (y, x);
- 2.
-
(x, y)(xy, z) = (y, z)(x, yz);
- 3.
-
(xs - t, xty) = (xt, y)-1(xs, y);
- 4.
-
(xs + p, y)t + p = (xs, y)t.
Д о к а з а т е л ь с т в о.
(1)
(x, y) = y-px-p(xy)p = x-py-p(yx[x, y])p = x-py-p(xy)p = (y, x).
(2) С одной стороны
(xyz)p = (xy)pzp(xy, z) = xpyp(x, y)zp(xy, z).
С другой --
(xyz)p = xp(yz)p(x, yz) = xpypzp(y, z)(x, yz) и
после приравнивания и сокращений получим (2).
(3) Следует из (2), если подставить xs - t вместо x,
xt вместо y и y вместо z.
(4) Следует из (2) леммы 1, так как
(x, y) 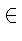 G' и
(xz, y) = (x, y), если z
G' и
(xz, y) = (x, y), если z 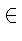 Z(G).
Z(G).
Лемма 3.
Если
a1,..., ap - 1 и
b1,..., bp - 1 -- элементы
аддитивной элементарной абелевой p-группы и
aj =
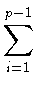 bi . ji
bi . ji, (
j = 1,...,
p - 1),
то
bi = -
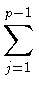 aj . jp - 1 - i
aj . jp - 1 - i, (
i = 1,...,
p - 1).
Д о к а з а т е л ь с т в о.
Условие леммы можно записать в виде
A = B . M, где
A = (a1,..., ap - 1) и
B = (b1,..., bp - 1) - "векторы", а
- матрица с элементами из Z/pZ. Пусть
Воспользовавшись тем, что
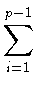 ip - 1
ip - 1 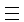
- 1mod
p,
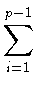 ir
ir 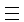
0mod
p
при
r 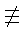 0modp-1 [1, 3.9.6],
легко проверить, что
M . N - единичная матрица и, значит,
B = A . N. Что и
требовалось доказать.
0modp-1 [1, 3.9.6],
легко проверить, что
M . N - единичная матрица и, значит,
B = A . N. Что и
требовалось доказать.
Лемма 4.
Пусть P -- свободная группа нильпотентного минимального не
p-регулярного многообразия со свободным
базисом {a, b}, и cl (P) = n.
Тогда
- 1.
-
(at, b) =
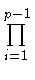 ui(a, b)ti, (t = 1,..., p - 1);
ui(a, b)ti, (t = 1,..., p - 1);
- 2.
-
(b, at) =
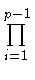 up - i(b, a)ti, (t = 1,..., p - 1);
up - i(b, a)ti, (t = 1,..., p - 1);
- 3.
-
ui(a, b) =
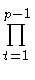 (at, b)-t(p - 1 - i), (i = 1,..., p - 1);
(at, b)-t(p - 1 - i), (i = 1,..., p - 1);
- 4.
-
up - i(b, a) =
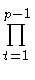 (b, at)-t(p - 1 - i), (i = 1,..., p - 1);
(b, at)-t(p - 1 - i), (i = 1,..., p - 1);
- 5.
-
u1(a, b) = up - 1(b, a);
- 6.
-
u1(a, atb)t =
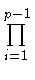 ui(a, b)
ui(a, b)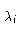 ti,
где
ti,
где
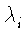 = (- 1)i - 1
= (- 1)i - 1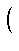
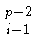
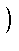 ,
(i = 1,..., p - 1),
(t = 1,..., p - 1).
,
(i = 1,..., p - 1),
(t = 1,..., p - 1).
- 7.
-
u1(a, b)
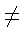 1,
up - 1(b, a)
1,
up - 1(b, a)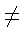 1.
1.
Д о к а з а т е л ь с т в о.
(1) Следует из определения ui(a, b) и (2) леммы 1.
(2) Так как
n 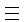 1modp-1 то,
как легко проверить, количество
вхождений a в коммутаторы из
up - i(b, a) сравнимо с i
по модулю p - 1.
Так как
1modp-1 то,
как легко проверить, количество
вхождений a в коммутаторы из
up - i(b, a) сравнимо с i
по модулю p - 1.
Так как
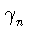 (P) элементарная абелева, (3) и (4)
следуют,
по лемме 3 из (1) и (2), соответственно.
(P) элементарная абелева, (3) и (4)
следуют,
по лемме 3 из (1) и (2), соответственно.
(5)
следует из (3)
и (4) так как
по (1) леммы 2
(a, b) = (b, a).
(6) В доказательстве этого пункта
будем использовать
для
элементов из
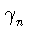 (P)
аддитивную запись.
Итак, по (4):
(P)
аддитивную запись.
Итак, по (4):
u1(
a,
atb) = -
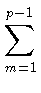
(
am,
atb)
mp - 2 = -
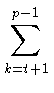 gk
gk -
gp -
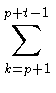 gk
gk,
где
gn = (ak - t, atb)(k - t)p - 2. По (4) леммы 2,
gk + p = gk и gt = 0. Поэтому
u1(
a,
atb) = -
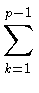 gk
gk -
gp.
По (1) леммы 2 и формуле бинома:
gk =
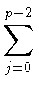
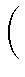
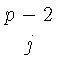
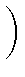
(-
t)
jkp - 2 - j((
ak,
b) - (
at,
b)), (
k = 1,...,
p - 1)
и
gp = - (at, b)(- t)p - 2
Воспользовавшись (3) и тем, что
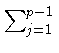 jr
jr 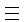 0mod p при
r
0mod p при
r 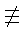 0modp-1
получим:
0modp-1
получим:
u1(a, atb) = - 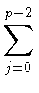 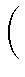 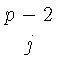
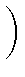 (- t)j (- t)j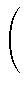 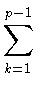 kp - 2 - j((ak, b) - (at, b)) kp - 2 - j((ak, b) - (at, b))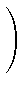 - gp =
- gp = |
= - 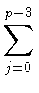 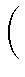 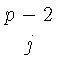
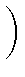 (- t)j (- t)j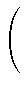 - uj + 1(a, b) - (at, b)
- uj + 1(a, b) - (at, b)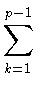 kp - 2 - j kp - 2 - j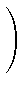 -
- |
- (- t)p - 2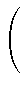 - up - 1(a, b) -
- up - 1(a, b) - 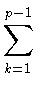 (at, b) (at, b)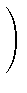 + (- t)p - 2(at, b) =
+ (- t)p - 2(at, b) = |
= 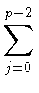  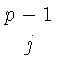
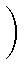 (- t)juj + 1(a, b). (- t)juj + 1(a, b). |
Отсюда легко получить (6) заменив j на i - 1.
(7) Достаточно показать, что
u1(a, b)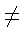 1
Если это не так, то поскольку {a, b} свободный базис,
u1(a, atb) = 1,
(t = 1,..., p - 1).
Отсюда по (6) и лемме 3
ui(a, b) = 1,
(i = 1,..., p - 1) и,
по (1) (a, b) = 1. Получили противоречие. Лемма доказана.
1
Если это не так, то поскольку {a, b} свободный базис,
u1(a, atb) = 1,
(t = 1,..., p - 1).
Отсюда по (6) и лемме 3
ui(a, b) = 1,
(i = 1,..., p - 1) и,
по (1) (a, b) = 1. Получили противоречие. Лемма доказана.
Д о к а з а т е л ь с т в о теоремы 1.
Рассуждая от противного, можно считать, что
наше многообразие минимальное не p-регулярное,
p - его свободная группа с
базисом {a, b}, cl (P) = n и
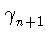 (P) . (P')p = 1.
По (7) леммы 4 следует, что для получения противоречия
достаточно показать, что
up - 1(a, b) = 1.
По определению
(P) . (P')p = 1.
По (7) леммы 4 следует, что для получения противоречия
достаточно показать, что
up - 1(a, b) = 1.
По определению
u1(a, b) = 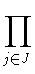 vj(a, b) vj(a, b) |
(1) |
где vj(a, b) простой коммутатор веса n в который a входит
1 + sj(p - 1) раз, а b входит mj(p - 1) раз и, поскольку
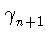 (G) . (G')p = 1,
можно считать, что
mj
(G) . (G')p = 1,
можно считать, что
mj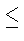 sj, то есть
sj, то есть
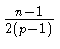 = S
= S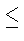 sj.
Подставив в тождество (1) x вместо a, zy вместо b и
применив стандартные коммутаторные соотношения, получим тождество
sj.
Подставив в тождество (1) x вместо a, zy вместо b и
применив стандартные коммутаторные соотношения, получим тождество
u1(x, zy) = 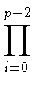 ki(x, y, z), ki(x, y, z), |
(2) |
где
ki(x, z, y) - произведение коммутаторов веса n, количество
вхождений x в которые сравнимо с 1 по модулю p - 1
и не меньше чем 1 + S(p - 1), а количество вхождений z сравнимо с i
по модулю p - 1.
Подставив в тождество (2) a вместо x, at вместо z и
b вместо y, получим
u1(a, atb) = 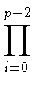 ki(a, b, a)ti (t = 1,..., p - 1). ki(a, b, a)ti (t = 1,..., p - 1). |
(3) |
или, что тоже самое,
u1(a, atb)t = 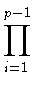 k(i - 1)(a, b, a)ti (t = 1,..., p - 1). k(i - 1)(a, b, a)ti (t = 1,..., p - 1). |
(4) |
Теперь поделив тождество (4) на тождество
(6) леммы 4,
получим
1 =
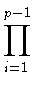
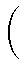 ki - 1
ki - 1(
a,
b,
a)
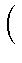 ui
ui(
a,
b)
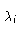 ti
ti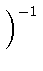
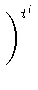
(
t = 1,...,
p - 1)
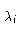 = 1.
Так как
u(p - 1)(a, b) = ui(a, b), нам осталось показать, что
kp - 2(a, b, a) = 1. Докажем, что
kp - 2(a, b, a)
состоит только из тех коммутаторов, которые лежат в
= 1.
Так как
u(p - 1)(a, b) = ui(a, b), нам осталось показать, что
kp - 2(a, b, a) = 1. Докажем, что
kp - 2(a, b, a)
состоит только из тех коммутаторов, которые лежат в
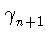 (G) . (G')p = 1.
Действительно, так как
количество вхождений a в каждый коммутатор
kp - 2(a, b, a)
из сравнимо с нулем по модулю p - 1, то
количество вхождений b в каждый коммутатор из
kp - 2(a, b, a)
сравнимо с 1 по модулю p - 1.
Заметим, что количество вхождений a больше чем
1 + (S(p - 1)) + (p + 2)
и, значит, по условию теоремы, коммутаторы из
kp - 2(a, b, a) лежат
в
(G) . (G')p = 1.
Действительно, так как
количество вхождений a в каждый коммутатор
kp - 2(a, b, a)
из сравнимо с нулем по модулю p - 1, то
количество вхождений b в каждый коммутатор из
kp - 2(a, b, a)
сравнимо с 1 по модулю p - 1.
Заметим, что количество вхождений a больше чем
1 + (S(p - 1)) + (p + 2)
и, значит, по условию теоремы, коммутаторы из
kp - 2(a, b, a) лежат
в
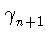 (G) . (G')p. Теорема доказана.
(G) . (G')p. Теорема доказана.
Д о к а з а т е л ь с т в о следствия 2.
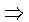 [7, 8.2.17].
Сначала заметим, что для свободной группы класса p
мы можем определить коммутаторные слова ui(a, b) точно
также как это сделано в (*). При этом
u1(a, b) = [a,
[7, 8.2.17].
Сначала заметим, что для свободной группы класса p
мы можем определить коммутаторные слова ui(a, b) точно
также как это сделано в (*). При этом
u1(a, b) = [a,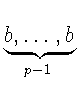 ].
Мы можем считать, что
].
Мы можем считать, что
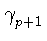 (G) . (G')p = 1.
В этом случае из p-регулярности G
следует, что в G выполняется тождество
(x[y, z])p = xp.
Используя рассуждения из доказательства (3) леммы 4,
легко показать, что в группе G выполняется тождество
u1(x, y) = 1, что и требовалось доказать.
(G) . (G')p = 1.
В этом случае из p-регулярности G
следует, что в G выполняется тождество
(x[y, z])p = xp.
Используя рассуждения из доказательства (3) леммы 4,
легко показать, что в группе G выполняется тождество
u1(x, y) = 1, что и требовалось доказать.
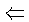 Как обычно, будем считать наше многообразие минимальным не
p-регулярным. Тогда для применения теоремы 1
достаточно доказать, что
Как обычно, будем считать наше многообразие минимальным не
p-регулярным. Тогда для применения теоремы 1
достаточно доказать, что
Ясно, что оба этих условия
выполняются, и p-регулярность G следует из теоремы 1.
Поступила 19.12.97
![]() G
G
![]() (P) p-абелева (так как она лежит в
собственном подмногообразии), то
(a, b)
(P) p-абелева (так как она лежит в
собственном подмногообразии), то
(a, b) ![]()
![]() (P),
и, значит, на P выполнено
(P),
и, значит, на P выполнено
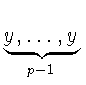 ]
] ![]() G и целых чисел s и t выполнено:
G и целых чисел s и t выполнено:
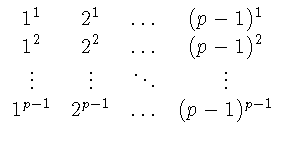
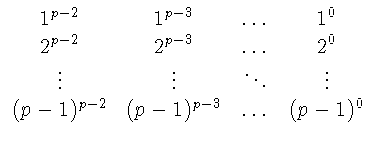
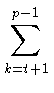 gk - gp -
gk - gp - 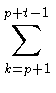 gk,
gk,
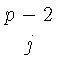
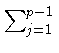 jr
jr 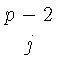
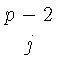
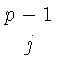
![]() (P) . (P')p = 1.
По (7) леммы 4 следует, что для получения противоречия
достаточно показать, что
up - 1(a, b) = 1.
По определению
(P) . (P')p = 1.
По (7) леммы 4 следует, что для получения противоречия
достаточно показать, что
up - 1(a, b) = 1.
По определению
![]() [7, 8.2.17].
Сначала заметим, что для свободной группы класса p
мы можем определить коммутаторные слова ui(a, b) точно
также как это сделано в (*). При этом
u1(a, b) = [a,
[7, 8.2.17].
Сначала заметим, что для свободной группы класса p
мы можем определить коммутаторные слова ui(a, b) точно
также как это сделано в (*). При этом
u1(a, b) = [a,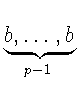 ].
Мы можем считать, что
].
Мы можем считать, что
![]() (G) . (G')p = 1.
В этом случае из p-регулярности G
следует, что в G выполняется тождество
(x[y, z])p = xp.
Используя рассуждения из доказательства (3) леммы 4,
легко показать, что в группе G выполняется тождество
u1(x, y) = 1, что и требовалось доказать.
(G) . (G')p = 1.
В этом случае из p-регулярности G
следует, что в G выполняется тождество
(x[y, z])p = xp.
Используя рассуждения из доказательства (3) леммы 4,
легко показать, что в группе G выполняется тождество
u1(x, y) = 1, что и требовалось доказать.
![]() Как обычно, будем считать наше многообразие минимальным не
p-регулярным. Тогда для применения теоремы 1
достаточно доказать, что
Как обычно, будем считать наше многообразие минимальным не
p-регулярным. Тогда для применения теоремы 1
достаточно доказать, что
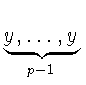 ]
] 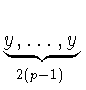 ]
]