ОТНОСИТЕЛЬНАЯ КОНСТАНТА ЮНГА
ПРОСТРАНСТВА

С. В. Бердышев

Аннотация:

В работе доказано, что относительная константа Юнга пространства , равна .

Пусть X - банахово пространство, V(X) - совокупность выпуклых ограниченных замкнутых множеств в X, состоящих более чем из одной точки. Для ограниченного множества M из X величина

есть диаметр множества M,

- его чебышевский радиус, а

- относительный чебышевский радиус. Если существуют точки на которых достигается нижняя грань в (1) и (2), то они называются соответственно чебышевским и относительным чебышевским центрами множества M.

Рассмотрим следующие характеристики пространства X:

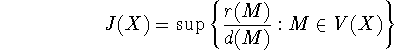
- константа Юнга пространства X,

- относительная константа Юнга и, наконец,

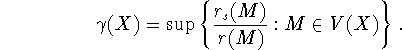
Легко видеть, что для всех верны неравенства

Отсюда, очевидно, следует, что

Юнг установил, что если X есть n-мерное евклидово пространство , то 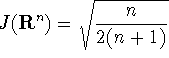(см. [5]). Как доказал Боненблюст, для любого n-мерного банахова пространства X справедливо неравенство и существуют пространства размерности n, для которых (см. [5]). Исследованием констант Юнга пространств занимались В.Л.Дольников (p = 1) [6], С.А.Пичугов () [7]. С.А.Пичугов вычислил константу Юнга пространств [7] и относительную константу Юнга пространств и для [8]. Кроме того, в [8] доказана оценка (числа p' и q' определяются соотношениями и соответственно)

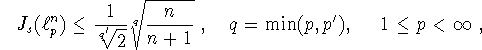
обращающаяся в равенство при p < 2 в случае n таких, что существует матрица Адамара размерности n+1. В. Кли (см. ссылку в [3, стр. 114,]) и А.Л. Гаркави [4] доказали, что чебышевский центр всякого ограниченного множества пространства X принадлежит выпуклой оболочке этого множества тогда и только тогда, когда X гильбертово или размерность X не превосходит двух. Более того, из доказательства этого факта следует, что эти же условия эквивалентны выполнению для пространства X равенства . Связь константы J с теоремой Джексона о наилучшем приближении отметил С.Б.Стечкин (см. [2]). Константы Юнга и геометрические свойства перестановочно-инвариантных пространств изучаются в [9]. Константа возникла в работе [1] В.В.Арестова, посвященной задаче о восстановлении операторов.

В пространстве имеет место следующее очевидное утверждение, из которого вытекает равенство .

Лемма 1. Для любого ограниченного множества M из пространства справедливо равенство

Лемма 2. Пусть есть выпуклая комбинация конечного числа точек пространства X. Тогда для любой точки y из X справедливо равенство

В самом деле, для любой точки существует набор неотрицательных чисел , сумма которых равна 1, такой, что . Тогда

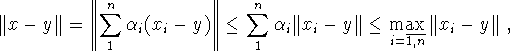
и это доказывает сформулированное утверждение.

В приводимой ниже теореме вычислена относительная константа Юнга пространства и описаны экстремальные множества, т. е. множества со свойством 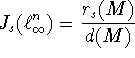. Очевидно, что если множество M является экстремальным, то для любой константы a > 0 и элемента множество x+aM также является экстремальным. Поэтому достаточно описать экстремальные множества с относительным чебышевским радиусом, равным единице, относительный чебышевский центр которых расположен в нуле. Для формулировки и доказательства этой теоремы нам понадобятся следующие обозначения. Назовем гранями единичного шара пространства множества вида

где . Две грани и будем называть противоположными. Пусть , где . Через M(E) обозначим выпуклую оболочку точек , координаты которых задаются равенствами



Поскольку , то . Точку с координатами обозначим через y(E). Через обозначим выпуклую оболочку

В случае, когда у набора E все координаты равны единице, для упрощения записи вместо будем писать и . Таким образом,

у точек k-я координата равна 1, а остальные координаты равны , есть выпуклая комбинация точек .

Теорема. Справедливо следующее равенство

Более того, при множество M с относительным чебышевским радиусом, равным единице, относительный чебышевский центр которого расположен в нуле, будет экстремальным в том и только в том случае, если найдется набор со свойством

Д о к а з а т е л ь с т в о. Заметим вначале, что для пространств размерности 2 чебышевский и относительный чебышевский радиусы ограниченных выпуклых множеств совпадают (см. [3]), и в силу леммы 1 равенство становится очевидным. Из этой же леммы следует, что экстремальным в этом случае будет любое множество .

Пусть теперь . Обозначим через совокупность множеств с относительным чебышевским радиусом, равным единице, относительный чебышевский центр которых расположен в нуле. И пусть . Ясно, что в определении величины можно ограничиться множествами M из . Поэтому утверждение теоремы эквивалентно равенству

Получим вначале оценку сверху для . Рассмотрим множества , и произвольное множество M, удовлетворяющее соотношениям . Учитывая лемму 2, легко видеть, что

Убедимся, что относительный чебышевский радиус множества M равен 1. Как отмечено выше, точка 0 принадлежит множеству , а значит, и множеству M. Поэтому имеет место неравенство . Возьмем произвольную не совпадающую с нулем точку . Поскольку множество M лежит в полупространстве , у точки y найдется координата . Тогда Значит,

0 есть относительный чебышевский центр множества M и для любого M со свойством .

Итак, отсюда и из (4) следует неравенство

Или, что то же самое, .

Докажем теперь обратное неравенство. В силу (4) и (5) множество лежит в , и . Поэтому в определении можно ограничиться совокупностью множеств со свойством

Получим оценку снизу величины d(M) для множеств (при ).

Пусть . Поскольку , то нет пары точек из M, принадлежащих двум противоположным граням . Покажем, что существует n попарно непротивоположных граней шара , на которых есть точки из M. В самом деле, пусть точки из множества M лежат лишь на k, где k < n, попарно непротивоположных гранях. Без ограничения общности будем считать, что эти точки принадлежат граням соответственно. Представим точки в координатной форме

Пусть . Тогда точка

принадлежит выпуклой оболочке точек , а значит, и множеству M.

Так как , то и . Поэтому все первые k координат , точек удовлетворяют неравенствам

Следовательно, первые k координат точки s удовлетворяют неравенствам

в частности, имеем для .

При сделанных выше предположениях относительно расположения множества M и граней единичного шара пространства можно утверждать, что расстояния между множеством M и гранями при для , а также при для положительные. Пусть - минимум из таких расстояний:

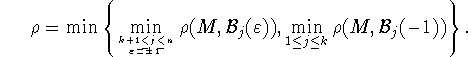
Таким образом, координаты произвольной точки из M удовлетворяют неравенствам

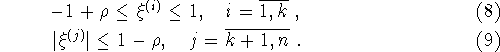
Выберем число , так, чтобы имели место неравенства

Тогда с учетом положительности при в силу (8) - (10) для любой точки будут верны следующие соотношения

Кроме того, из (10) получаем

Таким образом, множество M лежит в шаре с центром в точке , радиус которого строго меньше единицы. Это противоречит предположению, что .

Итак, на n попарно непротивоположных гранях , без ограничения общности, на гранях , лежат точки из множества M. Поскольку , то для произвольной точки из M выполняются неравенства и . Отсюда

Представим точки в координатной форме

Покажем теперь, что , и следовательно, . Для этого достаточно проверить, что все точки принадлежат гиперплоскости . Пусть это не так, т. е. одна из точек не лежит на указанной гиперплоскости. Тогда, вследствие (11), сумма ее координат больше ноля, а значит, одна из ее отличных от 1 координат больше, чем . Без ограничения общности будем считать, что у точки первая координата . Рассмотрим тогда . У этой точки первая координата положительна, а остальные неотрицательны. Далее, рассмотрим при точку . При любом достаточно близком к 1 значении параметра t все координаты точки z положительны. Действительно, для первой координаты это очевидно. Для i-й координаты () рассмотрим два случая: 1) и 2) . Случай 1) тривиален. Во втором случае i-я координата точки z оценивается снизу через сумму . Для точки z с положительными координатами точка принадлежит выпуклой комбинации , а следовательно, и множеству M. В силу неравенства (11) получаем

что приводит к противоречию с соотношением . Значит, , , и, следовательно,

Для завершения доказательства теоремы остается показать, что координаты любой точки из M удовлетворяют соотношению . Это легко устанавливается от противного. Действительно, если то множество вложено в M и содержит вектор при некотором . Тогда , что противоречит равенству . Значит, учитывая (11), мы имеем , и

Теорема полностью доказана.

Следствие. Имеет место равенство

Это утверждение является очевидным следствием теоремы и леммы 1.

Поступила 1.12.97

• Литература