где
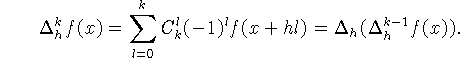
Он описал свойства
а для r раз непрерывно дифференцируемых периодических функций - справедливы неравенства
В. В. Арестов, В. И. Бердышев, Ю. Н. Субботин,
Н. И. Черных
22 ноября 1995 года ушел из жизни выдающийся математик Сергей Борисович Стечкин. В широком круге научных интересов профессора С.Б. Стечкина основное место занимают теория приближения функций и теория чисел. В теории приближения С.Б. Стечкин - признанный глава большой научной школы.
Первые работы С.Б. Стечкина [1, 2] относились к проблеме абсолютной
сходимости тригонометрических рядов и методам суммирования числовых
рядов. Но вскоре он увлекся вопросами теории приближения функций и в
1949 году опубликовал [3] (в [4] - с полными доказательствами)
неравенства, связывающие наилучшие
приближения ![]() непрерывных
непрерывных ![]() -периодических функций f
тригонометрическими полиномами порядки n-1 в равномерной метрике на
периоде с модулями непрерывности k-го порядка
-периодических функций f
тригонометрическими полиномами порядки n-1 в равномерной метрике на
периоде с модулями непрерывности k-го порядка ![]() этих функций,
этих функций,
![]()
где
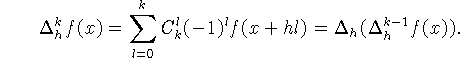
Он описал свойства ![]() и доказал, что при некоторой константе
и доказал, что при некоторой константе ![]() не
зависящей от n и f, справедливы неравенства
не
зависящей от n и f, справедливы неравенства
![]()
а для r раз непрерывно дифференцируемых периодических функций -
справедливы неравенства
![]()
Неравенства (1) и (2) при k=1 - это знаменитые неравенства
Д. Джексона, которые были доказаны им в 1911 г. В 1945 г.
А. Зигмунд
оценил скорость убывания ![]() при условии
при условии
![]() или
или ![]() В 1947 г.
С.Н. Бернштейн оценил скорость убывания
В 1947 г.
С.Н. Бернштейн оценил скорость убывания ![]() при условии, что
при условии, что
![]() а Н.И. Ахиезер доказал неравенство (1) при k=2.
Окончательную точку здесь поставил С.Б. Стечкин и неравенства (1), (2)
теперь называют неравенствами Джексона-Стечкина. Отметим, что методом
Джексона нельзя доказать (1) при k>2, так как положительный
полиномиальный оператор имеет порядок насыщения, равный 2.
С.Б. Стечкину пришлось разработать здесь существенно новый метод, а
построенный им класс полиномиальных операторов нашел
значительные применения в
дальнейшем.
а Н.И. Ахиезер доказал неравенство (1) при k=2.
Окончательную точку здесь поставил С.Б. Стечкин и неравенства (1), (2)
теперь называют неравенствами Джексона-Стечкина. Отметим, что методом
Джексона нельзя доказать (1) при k>2, так как положительный
полиномиальный оператор имеет порядок насыщения, равный 2.
С.Б. Стечкину пришлось разработать здесь существенно новый метод, а
построенный им класс полиномиальных операторов нашел
значительные применения в
дальнейшем.
В работах [3, 4] С.Б. Стечкин рассмотрел также
относящийся к тематике обратных теорем
теории приближения
вопрос о характеризации
периодических функций, допускающих заданную скорость убывания
наилучших приближений, в
терминах их свойств гладкости.
Первый результат, полностью согласующийся с
прямыми теоремами Джексона (см. (1), (2) при k=1) здесь был получен
С.Н. Бернштейном, доказавшим, что из условия ![]() вытекает непрерывная дифференцируемость
функции
f до порядка r включительно и вложение
вытекает непрерывная дифференцируемость
функции
f до порядка r включительно и вложение ![]() что вместе с теоремами
Джексона дает при
что вместе с теоремами
Джексона дает при ![]() эквивалентность
эквивалентность
![]()
Позже случай ![]() был охарактеризован А. Зигмундом в терминах
был охарактеризован А. Зигмундом в терминах ![]() Пусть
Пусть ![]() - класс
- класс ![]() -периодических
непрерывных функций, для которых
-периодических
непрерывных функций, для которых
![]()
где ![]() при некотором c>0 (иначе
класс
при некотором c>0 (иначе
класс ![]() содержит только константы), и пусть
содержит только константы), и пусть ![]() - класс таких
- класс таких ![]() удовлетворяющих дополнительному
условию:
удовлетворяющих дополнительному
условию: ![]() такое, что для
такое, что для ![]() выполняется неравенство
выполняется неравенство
![]()
Обозначим через ![]() полином
наилучшего приближения порядка n-1 для f в
полином
наилучшего приближения порядка n-1 для f в ![]() С.Б. Стечкин доказал, что
С.Б. Стечкин доказал, что
1) ![]() где C не зависит от n;
где C не зависит от n;
2) если ![]() то
то ![]()
3) если ![]() то
то ![]()
4) если ![]() то
то
![]()
(здесь ![]() знак порядкового равенства:
знак порядкового равенства: ![]() если при
некоторых абсолютных константах
если при
некоторых абсолютных константах ![]() и
и ![]() для всех значений A и B - функций от
для всех значений A и B - функций от ![]() или n).
или n).
В 1952 г. С.М. Лозинский доказал, что заключения теорем 3) и 4)
останутся справедливы, если в их посылках условие ![]() заменить на другое условие медленного роста функции
заменить на другое условие медленного роста функции ![]() а именно
на условие
а именно
на условие ![]() такое, что
такое, что
![]()
и доказал, что при
этом последние условия нельзя ослабить, не нарушив импликаций
![]()
Позже С.Б. Стечкин и Н.К. Бари
[13] доказали, что условия Стечкина и Лозинского в этих теоремах
эквивалентны.
Неравенства (1), (2) Джексона-Стечкина были распространены (с
существенным использованием его метода) на метрики ![]() на
разные метрики
(т.е. при естественных ограничениях получены
оценки наилучших приближений
на
разные метрики
(т.е. при естественных ограничениях получены
оценки наилучших приближений ![]() функций f в
функций f в
![]() через модули непрерывности
через модули непрерывности ![]() в
в ![]() на дробные в смысле Вейля производные, на приближения функций нескольких
переменных, на наилучшие приближения целыми функциями
экспоненциального типа, на модули непрерывности дробного порядка.
Тематика нашла продолжение в комонотонных и ковыпуклых
приближениях, приближениях функций сплайнами и полиномами по
другим системам функций (В.К. Дзядык, А.Ф. Тиман, М.Ф. Тиман,
А.С. Шведов, И.А. Шевчук и др.).
на дробные в смысле Вейля производные, на приближения функций нескольких
переменных, на наилучшие приближения целыми функциями
экспоненциального типа, на модули непрерывности дробного порядка.
Тематика нашла продолжение в комонотонных и ковыпуклых
приближениях, приближениях функций сплайнами и полиномами по
другим системам функций (В.К. Дзядык, А.Ф. Тиман, М.Ф. Тиман,
А.С. Шведов, И.А. Шевчук и др.).
Неравенство (2) связывает величины ![]() и гладкость производной
и гладкость производной
![]() Из него следует также оценка
Из него следует также оценка ![]() непосредственно через
непосредственно через ![]() Известны и точные оценки
такого рода:
Известны и точные оценки
такого рода:
![]()
где ![]() - функция, тригонометрически сопряженная к f,
- функция, тригонометрически сопряженная к f,
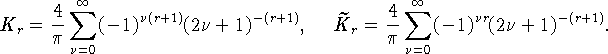
Неравенства точные на классах ![]() и
и ![]() периодических
функций с непрерывными производными
периодических
функций с непрерывными производными ![]() и
и ![]() Это результаты Ж. Фавара, Н.И. Ахиезера - М.Г. Крейна 1936 -
1937 годов, точнее, это тривиальные следствия из их неравенств
Это результаты Ж. Фавара, Н.И. Ахиезера - М.Г. Крейна 1936 -
1937 годов, точнее, это тривиальные следствия из их неравенств
![]()
В работах [4], [5] С.Б. Стечкин получил в некотором роде обратные
к этим
оценки. Именно, справедлива теорема: если ряд ![]() сходится (r - целое неотрицательное), то существуют непрерывные
производные
сходится (r - целое неотрицательное), то существуют непрерывные
производные ![]() (это результат С.Н. Бернштейна) и
(это результат С.Н. Бернштейна) и
![]() и выполняются неравенства
и выполняются неравенства
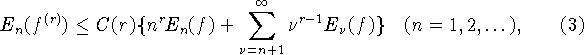
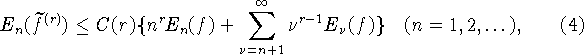
точные по порядку на классах функций f, определяемых условиями
![]()
где
![]()
Эти неравенства получили название
обратных теорем Стечкина и также обобщались в самых различных
направлениях.
В работе [6] С.Б. Стечкин рассмотрел классы периодических
функций ![]() и
и
![]() - вещественное).
Эти классы определяются
посредством ядер
- вещественное).
Эти классы определяются
посредством ядер
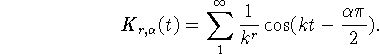
следующим образом:
![]()
![]()
Классы функций ![]() и
и ![]() являются обобщениями
классов
являются обобщениями
классов ![]() и
и ![]() периодических функций, у которых
нормы производных по Вейлю порядка
периодических функций, у которых
нормы производных по Вейлю порядка ![]() ограничены,
соответственно, в
ограничены,
соответственно, в
![]() и
и ![]() константой 1.
При некоторых r и
константой 1.
При некоторых r и ![]() он вычислил наилучшие приближения
он вычислил наилучшие приближения
![]()
этих классов тригонометрическими полиномами порядка n-1. До него кроме
указанных выше результатов Ж. Фавара, Н.И. Ахиезера - М.Г. Крейна
здесь были
известны результаты С.М. Никольского, Б.-С. Надя,
а также результат В.К. Дзядыка, доказавшего,
что при 0<r<1
![]()
где
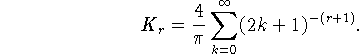
Указанный результат С.Б. Стечкина ближе примыкает к последнему результату и
состоит в следующем: если ![]() то
то
![]()
Отсюда, в частности, вытекает, что при ![]()
![]()
В связи с результатом Н.П. Корнейчука, нашедшего точную константу в
неравенстве Джексона (1) (k=1)
![]()
где 1 в правой части нельзя уменьшить, сохраняя неравенство верным
при всех ![]() и
и ![]() -периодическая), С.Б. Стечкин [10] доказал замечательное
неравенство:
-периодическая), С.Б. Стечкин [10] доказал замечательное
неравенство:
![]()
справедливое для каждой ![]() -периодической функции
-периодической функции ![]() где
где ![]() и
и ![]() - наилучшее
приближение тригонометрическими полиномами порядка n-1 и модуль
непрерывности функции f в
- наилучшее
приближение тригонометрическими полиномами порядка n-1 и модуль
непрерывности функции f в ![]() и указал положительный линейный
метод приближения, обеспечивающий эту оценку.
и указал положительный линейный
метод приближения, обеспечивающий эту оценку.
Известны глубокие результаты С.Б. Стечкина, относящиеся к проблеме
абсолютной сходимости тригонометрических рядов, к проблеме поведения
наилучших приближений функций, представимых лакунарными рядами, к
оценкам норм полиномиальных операторов, определяемых последовательностью
множителей перед гармониками полиномов, в частности, об асимптотике
констант Лебега и Валле-Пуссена для частных сумм рядов Фурье и их
средних Фейера и Валле-Пуссена, его результаты в задаче оценки
уклонений частных сумм порядка n рядов Фурье функций классов
![]() равномерной по всем параметрам
равномерной по всем параметрам ![]() результаты по
приближению рядами Тейлора-Маклорена, а также в проблеме экстремальных
свойств тригонометрических полиномов и классов функций.
результаты по
приближению рядами Тейлора-Маклорена, а также в проблеме экстремальных
свойств тригонометрических полиномов и классов функций.
В недавней работе [11] С.Б. Стечкин вновь вернулся к проблематике прямых
и обратных теорем теории приближения функций. В этой работе он описал
широкий класс систем функций ![]() на которые
переносятся многие результаты для наилучших приближений
тригонометрическими полиномами из серии прямых и обратных теорем.
на которые
переносятся многие результаты для наилучших приближений
тригонометрическими полиномами из серии прямых и обратных теорем.
Во всех этих работах С.Б. Стечкина отличает филигранная аналитическая
техника, богатство идей и выбор методов решения, наиболее адекватных
задачам. Хотя, конечно, это ему удавалось не всегда. Так, комментируя
свою точную по порядку оценку колмогоровских поперечников классов
![]() периодических функций снизу, он сетовал после
вычисления этих поперечников В.М.Тихомировым, что вот он "вставлял в
компактный класс
периодических функций снизу, он сетовал после
вычисления этих поперечников В.М.Тихомировым, что вот он "вставлял в
компактный класс ![]() "ежа" и не догадался
вставить "гладенький шарик", как это сделал Тихомиров.
Но даже этот пример демонстрирует
многообразие его идей и подходов (ведь "вставлял" же!), которые будут
еще развиваться и способствовать развитию теории функций.
"ежа" и не догадался
вставить "гладенький шарик", как это сделал Тихомиров.
Но даже этот пример демонстрирует
многообразие его идей и подходов (ведь "вставлял" же!), которые будут
еще развиваться и способствовать развитию теории функций.
С.Б. Стечкин, виртуозный мастер тонких аналитических выкладок, всегда проявлял тягу к геометрической проблематике. Период 50-х и 60-х годов - время его активного интереса к геометрической теории приближения, в основном, в связи с проблемой выпуклости чебышевских множеств в гильбертовом пространстве, которая была сформулирована им и Н.В. Ефимовым одновременно с В. Кли (1961 г.). Имеющиеся к этому моменту геометрические результаты касались преимущественно конечномерных евклидовых пространств (см. [23, 25]). По инициативе С.Б. Стечкина и Н.В. Ефимова в нашей стране проводились исследования по геометрической тематике для произвольных, в том числе бесконечномерных, пространств по крайней мере по трем аспектам:
а) взаимосвязь геометрических и аппроксимативных характеристик множеств в банаховых пространствах (если множество чебышевское или является солнцем, то будет ли оно выпуклым?);
б) насколько богаты в смысле плотности, категории, меры
и т.п. множества точек пространства, для которых существует хотя бы
один, или имеется не более одного, или существует единственный
ближайший элемент из заданного множества ![]() ?
?
в) как влияют свойства пространства X на аппроксимативные характеристики множеств из X?
Благодаря С.Б. Стечкину и Н.В. Ефимову в обиход прочно вошли понятия: чебышевское множество, солнце, множество существования, множество единственности и т.д.
Пусть X - линейное нормированное пространство, M - множество из
![]()
![]() - расстояние от
x до M,
- расстояние от
x до M,
![]()
- множество элементов
наилучшего приближения. Множество M называется множеством
существования (единственности, соответственно, чебышевским), если
множество ![]() не пусто (не более чем одноточечно, соответственно,
одноточечно) для любого
не пусто (не более чем одноточечно, соответственно,
одноточечно) для любого ![]() П.Л. Чебышев показал, что для любой
функции
П.Л. Чебышев показал, что для любой
функции ![]() множество
множество ![]() одноточечно, в случае, когда
одноточечно, в случае, когда
![]() - множество алгебраических многочленов степени не более
- множество алгебраических многочленов степени не более
![]() или
или ![]() - множество дробей
- множество дробей
![]() В терминологии Н.В. Ефимова
и С.Б. Стечкина множества
В терминологии Н.В. Ефимова
и С.Б. Стечкина множества ![]() являются
чебышевскими множествами в пространстве C[a, b]. Изучение чебышевских
множеств привело их к новому и, как позже выяснилось, важному понятию
аппроксимативной компактности. Множество
являются
чебышевскими множествами в пространстве C[a, b]. Изучение чебышевских
множеств привело их к новому и, как позже выяснилось, важному понятию
аппроксимативной компактности. Множество ![]() называется
аппроксимативно компактным, если для любого
называется
аппроксимативно компактным, если для любого ![]() и любой
минимизирующей последовательности
и любой
минимизирующей последовательности ![]() (т.е. такой, что
(т.е. такой, что ![]() ) существует подпоследовательность
) существует подпоследовательность ![]() сходящаяся к некоторому элементу
сходящаяся к некоторому элементу ![]() Это понятие работает, в
частности, в следующей характеризационной теореме Н.В. Ефимова и
С.Б. Стечкина:
для чебышевского множества M в гладком равномерно
выпуклом банаховом пространстве следующие условия эквивалентны:
Это понятие работает, в
частности, в следующей характеризационной теореме Н.В. Ефимова и
С.Б. Стечкина:
для чебышевского множества M в гладком равномерно
выпуклом банаховом пространстве следующие условия эквивалентны:
![]() выпукло;
выпукло;
![]() аппроксимативно компактно;
аппроксимативно компактно;
![]() секвенциально слабо замкнуто.
секвенциально слабо замкнуто.
Н.В. Ефимов и С.Б. Стечкин установили, что множество дробей ![]() в пространстве
в пространстве ![]() аппроксимативно компактно,
и поскольку
аппроксимативно компактно,
и поскольку ![]() не выпукло, то это множество
не выпукло, то это множество ![]() по критерию не является чебышевским в
по критерию не является чебышевским в ![]() Тем самым они
дали пример использования введенного понятия для конкретных
пространств.
Тем самым они
дали пример использования введенного понятия для конкретных
пространств.
И. Зингер [31] ввел класс пространств Ефимова-Стечкина, в которых каждое секвенциально слабо замкнутое множество является аппроксимативно компактным (что эквивалентно условию: каждое выпуклое замкнутое множество аппроксимативно компактно). Пространства Ефимова-Стечкина важны не только для теории приближений (см., напр., [23], но и для многих смежных разделов математики: обоснование методов регуляризации некорректных задач [18], устойчивость решений экстремальных задач (см., напр., [21]), существование неподвижных точек отображений [24] и др.
В связи с упомянутым выше направлением исследований б) приведем
обозначения, здесь ![]()
![]() пусто или одноточечно
пусто или одноточечно ![]()
![]() одноточечно
одноточечно ![]()
С.Б. Стечкин показал [7], что банахово пространство X строго выпукло
тогда и только тогда, когда для любого ![]() множество
множество ![]() является дополнением множества первой категории (в частности, плотно в
X). Эти результаты С.Б. Стечкина стимулировали исследования множеств
точек пространства со специальными аппроксимативными свойствами
(С.В. Конягин, П.С. Кендеров, Л. Заячек и др.).
является дополнением множества первой категории (в частности, плотно в
X). Эти результаты С.Б. Стечкина стимулировали исследования множеств
точек пространства со специальными аппроксимативными свойствами
(С.В. Конягин, П.С. Кендеров, Л. Заячек и др.).
С.Б. Стечкин поддерживал работу по изучению вопросов непрерывности,
слабой непрерывности,
равномерной непрерывности, сильной единственности, дифференцируемости
оператора метрического проектирования ![]() в общих и
специальных пространствах (В.С. Балаганский, В.И. Бердышев, Л.П. Власов,
А.В. Колушов, А. Кроо, А.В. Маринов, И.Г. Царьков).
в общих и
специальных пространствах (В.С. Балаганский, В.И. Бердышев, Л.П. Власов,
А.В. Колушов, А. Кроо, А.В. Маринов, И.Г. Царьков).
Непосредственным обобщением классической задачи П.Л. Чебышева о приближении функций многочленами является задача аппроксимации обобщенными полиномами непрерывных на компакте функций со значениями в банаховом пространстве. С.Б. Стечкин совместно с С.И. Зуховицким в случае строго выпуклого пространства установил критерий полинома наилучшего приближения и критерий единственности.
Важное место в исследованиях С.Б. Стечкина и его Школы по теории приближения
занимает задача о наилучшем приближении неограниченного линейного оператора
линейными ограниченными операторами на классе элементов банахова
пространства. Эту задачу в настоящее время называют задачей Стечкина.
Она появилась в исследованиях С.Б. Стечкина в 1965 году [8].
Его работа [9] 1967 года содержит постановку задачи,
первые принципиальные результаты и
ее решение для операторов дифференцирования
малого порядка.
Точная постановка задачи такова.
Пусть ![]() - банаховы пространства;
- банаховы пространства; ![]() -
некоторый линейный оператор
с областью определения
-
некоторый линейный оператор
с областью определения ![]() - некоторый класс элементов из D(A);
- некоторый класс элементов из D(A);
![]() - множество
линейных ограниченных операторов из X в Y, норма которых
- множество
линейных ограниченных операторов из X в Y, норма которых
![]() не превосходит
числа
не превосходит
числа ![]() Величина
Величина
![]()
является уклонением оператора ![]() от оператора A
на классе Q, а
от оператора A
на классе Q, а
![]()
есть наилучшее приближение оператора A множеством
ограниченных операторов ![]() на классе Q. Задача
состоит в вычислении (исследовании) величины E(N),
нахождении (исследовании вопросов существования, единственности,
характеризации) экстремального оператора,
на котором в (5) достигается нижняя грань.
на классе Q. Задача
состоит в вычислении (исследовании) величины E(N),
нахождении (исследовании вопросов существования, единственности,
характеризации) экстремального оператора,
на котором в (5) достигается нижняя грань.
С.Б. Стечкин [9]
дал простую, но часто используемую и эффективную оценку снизу
![]()
величины наилучшего приближения E(N)
через модуль непрерывности
![]()
оператора A на классе Q.
Именно это неравенство Стечкина применялось в большинстве работ,
содержащих решение задачи (5).
Первый точный результат в задаче (5) получил С.Б. Стечкин.
Он дал [9], [8] решение этой задачи
для операторов дифференцирования ![]() порядка k
на классе
порядка k
на классе ![]() раз дифференцируемых функций
в пространстве C(S) непрерывных ограниченных функций на
оси
раз дифференцируемых функций
в пространстве C(S) непрерывных ограниченных функций на
оси ![]() и полуоси
и полуоси ![]() для значений
n=2 и
для значений
n=2 и ![]() в частности, выписал для этих
случаев экстремальные операторы
в частности, выписал для этих
случаев экстремальные операторы ![]() А именно, он показал, что
на оси
А именно, он показал, что
на оси ![]() экстремальными являются операторы
экстремальными являются операторы
![]()
![]()
а на полуоси ![]() таковыми являются операторы
таковыми являются операторы
![]()
![]()
![]()
здесь h положительный параметр.
С.Б. Стечкин понял также (см.,например, работы [19-20]),
что задача (5) взаимосвязана
с некорректной задачей оптимального
восстановления значений оператора A на элементах класса Q,
заданных с (известной) ошибкой ![]() Пусть
Пусть ![]() есть либо множество
есть либо множество
![]() всех (однозначных) отображений пространства
X в пространство Y,
либо множество
всех (однозначных) отображений пространства
X в пространство Y,
либо множество
![]() линейных операторов из X в Y.
Для числа
линейных операторов из X в Y.
Для числа ![]() и оператора
и оператора ![]() полагаем
полагаем
![]()
Тогда
![]()
есть величина наилучшего восстановления (наименьшая погрешность
восстановления) оператора A
с помощью множества отображений (методов восстановления)
![]() на элементах класса Q,
заданных с погрешностью
на элементах класса Q,
заданных с погрешностью ![]() С.Б. Стечкин заметил, что
имеют место неравенства
С.Б. Стечкин заметил, что
имеют место неравенства
![]()
В частности, он установил, что операторы (8) - (12)
дают оптимальные (наилучшие) формулы
численного дифференцирования функций соответствующих
классов ![]() , заданных с погрешностью
, заданных с погрешностью ![]() (при определенной связи между параметрами h и
(при определенной связи между параметрами h и ![]() ).
).
Публикация работы С.Б. Стечкина [9], его неоднократные выступления с научными докладами и лекциями на Конференциях и Школах по теории приближения, начиная с 1965 года, и, особенно, многократные обсуждения задачи (5) на руководимом С.Б. Стечкиным семинаре в Свердловском отделении Математического института им В.А. Стеклова АН СССР (ныне Институт математики и механики УрО РАН) в 1965 - 1967 годах, способствовали развитию этой проблематики и превращению ее в интенсивно развивающееся, содержательное направление исследований в теории функций. Существенный вклад в развитие этой тематики наряду с С.Б. Стечкиным внесли ученики С.Б. Стечкина и участники его Семинаров - Л.В. Тайков, Ю.Н. Субботин, Н.И. Черных, В.Н. Габушин, В.В. Арестов, В.И. Бердышев, О.А. Тимошин. На развитие этой тематики большое влияние оказали тонкие результаты по точным неравенствам между нормами производных дифференцируемых функций (неравенствам Колмогорова) В.М. Тихомирова и его учеников А.П. Буслаева, Б.Е. Клоца, Г.Г. Магарил-Ильяева.
К настоящему времени в задаче Стечкина получены следующие результаты.
Выяснена взаимосвязь этой задачи с другими экстремальными задачами.
В дополнение к соотношениям (6), (14) С.Б. Стечкина
между модулем непрерывности линейного неограниченного оператора,
наилучшим приближением
такого оператора линейными ограниченными операторами и
некорректной задачей оптимального равномерного
восстановления значений оператора на
элементах класса в предположении, что эти элементы заданы неточно
(с известной погрешностью), установлены естественные двусторонние
неравенства, связывающие
E(N) и ![]() а также
а также
![]() и
и ![]() Получены двойственные соотношения между
модулем непрерывности
Получены двойственные соотношения между
модулем непрерывности ![]() оператора
и наилучшим приближением одного класса элементов другим,
а также между E(N)
и наилучшим линейным приближением класса классом.
Получен ряд общих теорем существования и характеризации
экстремального приближающего оператора в задачах (5) и (13).
Обстоятельно изучено наилучшее приближение функционалов.
Подробно исследовано приближение операторов,
инвариантных относительно некоторых
полугрупп (групп) преобразований. Более полно и результативно
изучено наилучшее приближение операторов,
инвариантных относительно сдвига,
в пространствах
оператора
и наилучшим приближением одного класса элементов другим,
а также между E(N)
и наилучшим линейным приближением класса классом.
Получен ряд общих теорем существования и характеризации
экстремального приближающего оператора в задачах (5) и (13).
Обстоятельно изучено наилучшее приближение функционалов.
Подробно исследовано приближение операторов,
инвариантных относительно некоторых
полугрупп (групп) преобразований. Более полно и результативно
изучено наилучшее приближение операторов,
инвариантных относительно сдвига,
в пространствах ![]() Дано решение задачи для конкретных операторов
в классических функциональных пространствах. При этом наиболее полно
исследовано наилучшее приближение операторов дифференцирования
порядка k на
классе n раз дифференцируемых функций
Дано решение задачи для конкретных операторов
в классических функциональных пространствах. При этом наиболее полно
исследовано наилучшее приближение операторов дифференцирования
порядка k на
классе n раз дифференцируемых функций ![]() в пространствах
в пространствах ![]() на числовой оси
на числовой оси ![]() и
полуоси
и
полуоси ![]() На этом пути найдены
наилучшие константы в неравенствах Колмогорова в ряде новых случаев.
Вычислено наилучшее приближение операторов дифференцирования
в частных производных на классах функций многих переменных в ряде случаев.
Обзор результатов по этой тематике можно найти в работе [20].
На этом пути найдены
наилучшие константы в неравенствах Колмогорова в ряде новых случаев.
Вычислено наилучшее приближение операторов дифференцирования
в частных производных на классах функций многих переменных в ряде случаев.
Обзор результатов по этой тематике можно найти в работе [20].
Отличительной чертой научной деятельности Сергея Борисовича являлось то, что он всегда целеустремленно содействовал развитию новых направлений, в том числе и теории сплайнов. Этому способствовало и его умение ставить острые проблемные задачи. У С.Б. Стечкина практически нет индивидуальных работ по теории сплайнов. Лишь однажды он делал доклад по этой теме на конференции по теории функций в 1983 году в Днепропетровске. В нем речь шла о построении интерполяционных кусочно полиномиальных функций на сгущающихся хаотических сетках. Был предложен метод интерполяции, обеспечивающий безусловную (без дополнительных условий на последовательность сеток кроме естественного - диаметр разбиения стремится к нулю) равномерную сходимость к функции и производным кусочно полиномиальных функций и соответствующих их производных по второй порядок включительно. При этом сходимость обеспечивалась на классе функций с непрерывными частными производными второго порядка. Насколько известно, доклад не был опубликован.
Тем не менее роль С.Б. Стечкина в развитии теории сплайнов была значительной. Он не только поддерживал и направлял исследования в этой области своих учеников и учеников учеников (Ю.Н. Субботин, Н.И. Черных, П.В. Галкин, Ал.А. Привалов, А.Ю. Шадрин, Н.Л. Зматраков, В.Т. Шевалдин, С.И. Новиков, и др.), но и ряда других математиков (Ю.С. Завьялов, А.А. Женсыкбаев и др.). Кроме того в 60-х годах он сформулировал ряд экстремальных задач, решение которых естественным образом приводило к сплайнам. Он активно пропагандировал сплайны и всегда настойчиво приглашал выступить с докладом на своем научном семинаре в МИ АН СССР им. В.А. Стеклова и своих учебных семинарах на механико-математическом факультете МГУ специалистов по сплайнам, приезжавших в Москву.
На развитие теории сплайнов большое влияние оказала задача
Н.Н. Яненко, сформулированная С.Б. Стечкиным в 1960 г. в экстремальной
постановке: найти величину
![]()
где ![]() берется по всем функциям с локально абсолютно непрерывной
(n-1)-й производной, удовлетворяющим условиям
берется по всем функциям с локально абсолютно непрерывной
(n-1)-й производной, удовлетворяющим условиям ![]() а
а ![]() - по всем последовательностям
- по всем последовательностям ![]() удовлетворяющим
условию
удовлетворяющим
условию ![]()
Кроме того он высказал две гипотезы:
1) Наихудшей последовательностью будет последовательность
![]()
2) Величина ![]()
Первая гипотеза полностью подтвердилась. Вторая подтвердилась лишь при n=1,2,3, (см. [27]).
В дальнейшем эта задача обобщалась в различных направлениях в работах Ю.Н. Субботина, А. Шармы, И. Цимбаларио и В.Т. Шевалдина. Кстати, во всех обобщениях в случае конечности соответствующей величины всегда выполнялась первая гипотеза С.Б. Стечкина, что облегчало решение задачи. При решении задачи (15) и ее аналогов для дифференциальных операторов естественным образом возникали полиномиальные и L-сплайны. При этом найденные явные представления для таких сплайнов в значительной степени способствовали изучению их аппроксимативных свойств. В частности, решение задачи (15) способствовало правильному определению интерполяционных сплайнов четной степени.
Сергей Борисович высоко оценивал перспективы теории сплайнов в теоретической и прикладной математике и поэтому предпринял большие усилия по организации перевода книги Дж. Алберга, Э. Нильсона и Дж. Уолша "Теория сплайнов и ее приложения". Задача состояла в том, кому доверить перевод книги. Человеку, знающему английский, но не знающему сплайнов или наоборот. С.Б. Стечкин убедил редакцию издательства "Мир" выбрать второй вариант. Выбор пал на одного из авторов этой заметки - Ю.Н.Субботина. Первый пробный перевод нескольких страничек был ужасен. Тем не менее Сергей Борисович убедил редакцию дать еще одну попытку. Второй пробный перевод удовлетворил редакцию, Возникла проблема перевода английского термина "spline" на русский язык. Существовал термин "многозвенные функции", введенный Ю.С. Завьяловым. С.Б. Стечкину он не понравился, так как больше отражал понятие "кусочно линейные функции", но в то же время более подходящего термина в русском языке мы не нашли. По-видимому, мы настолько привыкли к слову "сплайн", что оно не резало нам слух, и мы продолжали настаивать на его сохранении в русском языке. Основное возражение редакции состояло в том, что в русском языке нет ни одного слова, заканчивающегося на "айн". После такого ответа, был приведен контрпример: "комбайн". Последняя проблема была снята и перевод появился.
К переводу С.Б. Стечкин и Ю.Н. Субботин написали добавление [12], в
котором содержались и оригинальные результаты указанных авторов. В
частности, существенно усилен пример С. Норда к проблеме И. Шоенберга
о расходимости интерполяционных сплайнов. В связи с этим примером по
инициативе С.Б. Стечкина мы потратили значительные усилия, чтобы
охарактеризовать тот класс функций, для которого последовательность
интерполяционных кубических (параболических, правильное определение
которых было дано в Добавлениях) безусловно сходится к любой функции
из этого класса. Однако несколько лет спустя ученик С.Б. Стечкина
Ал.А. Привалов усилил наш пример расходимости. В итоге из
положительных результатов С.Б. Стечкина-Ю.Н. Субботина и контрпримера
Ал.А. Привалова вытекал следующий результат:
для того чтобы для непрерывной периодической функции имела место
безусловная сходимость интерполяционных параболических (кубических)
сплайнов, необходимо и достаточно, чтобы она принадлежала классу
![]()
В 1973 г. в связи с обсуждением докторской диссертации Ю.С. Завьялова
в СОМИ АН СССР (ныне ИММ УрО РАН) возникла задача о нахождении
окончательных условий на параметр ![]() фигурирующий в локальных
условиях на узлы интерполяции кубического сплайна, обеспечивающих
равномерную сходимость таких сплайнов на классе непрерывных функций.
Эти условия были найдены Н.Л. Зматраковым. Он же нашел окончательные
условия на p в случае, когда рассматриваемые функции принадлежат
классу
фигурирующий в локальных
условиях на узлы интерполяции кубического сплайна, обеспечивающих
равномерную сходимость таких сплайнов на классе непрерывных функций.
Эти условия были найдены Н.Л. Зматраковым. Он же нашел окончательные
условия на p в случае, когда рассматриваемые функции принадлежат
классу ![]() . Последняя задача была сформулирована С.Б. Стечкиным.
. Последняя задача была сформулирована С.Б. Стечкиным.
В 1975 году С.Б. Стечкин предложил Ю.Н. Субботину написать совместную книгу
по теории сплайнов. В 1976 году книга
"Сплайны в вычислительной математике" вышла в свет [17]. В качестве одной
из важных задач при написании книги С.Б. Стечкин считал ее широкую
доступность. В частности, по этой причине мы ограничились в оценках
погрешности аппроксимации лишь равномерной, ![]() и
и ![]() метриками. Другой
важной задачей он считал необходимость проиллюстрировать, хотя бы на
простейших примерах, возможность применения сплайнов в различных задачах
вычислительной математики.
метриками. Другой
важной задачей он считал необходимость проиллюстрировать, хотя бы на
простейших примерах, возможность применения сплайнов в различных задачах
вычислительной математики.
В книге детально исследовались определяющие уравнения
для интерполяционных параболических сплайнов с различными краевыми
условиями и различным расположением узлов сплайна и узлов интерполяции,
а также аппроксимативные свойства таких сплайнов.
Далее кратко изложены основные
результаты по аппроксимативным свойствам кубических сплайнов. В
частности, доказан упоминавшийся выше результат о безусловной
сходимости кубических сплайнов для функций из класса ![]() В
заключительной части главы приведены результаты по многомерным
параболическим сплайнам. Здесь, пожалуй, важно отметить, что
С.Б. Стечкин всегда обращал внимание на важность многомерных задач.
Далее изложены известные результаты по аппроксимативным
свойствам сплайнов произвольной степени с равномерными узлами. Новым
здесь можно считать лишь заключительный параграф, посвященный
многомерным сплайнам с равномерными узлами.
Кроме того, в книге обсуждаются проблемы
наилучшего среднеквадратического и равномерного приближения сплайнами
с фиксированными узлами и классические варианты проблемы сглаживания,
берущие свое начало с работы Рейнша, в том числе
модельная проблема сглаживания для функции двух переменных.
Заключительная глава книги посвящена применению сплайнов в численном
анализе. Здесь в модельном случае дано точное решение задачи
С.Б. Стечкина о наилучшем приближении оператора дифференцирования линейными
ограниченными операторами и задачи наилучшего численного
дифференцирования при информации, известной с погрешностью. Здесь же
впервые рассмотрены подобные экстремальные задачи, когда значения
функции известны (точно или с погрешностью) лишь на сетке. Кроме того
в этой главе предложен алгоритм для построения интерполяционного
параболического сплайна в случае, когда интерполируемая функция
y(x) задана на отрезке [a, b] неявным уравнением
В
заключительной части главы приведены результаты по многомерным
параболическим сплайнам. Здесь, пожалуй, важно отметить, что
С.Б. Стечкин всегда обращал внимание на важность многомерных задач.
Далее изложены известные результаты по аппроксимативным
свойствам сплайнов произвольной степени с равномерными узлами. Новым
здесь можно считать лишь заключительный параграф, посвященный
многомерным сплайнам с равномерными узлами.
Кроме того, в книге обсуждаются проблемы
наилучшего среднеквадратического и равномерного приближения сплайнами
с фиксированными узлами и классические варианты проблемы сглаживания,
берущие свое начало с работы Рейнша, в том числе
модельная проблема сглаживания для функции двух переменных.
Заключительная глава книги посвящена применению сплайнов в численном
анализе. Здесь в модельном случае дано точное решение задачи
С.Б. Стечкина о наилучшем приближении оператора дифференцирования линейными
ограниченными операторами и задачи наилучшего численного
дифференцирования при информации, известной с погрешностью. Здесь же
впервые рассмотрены подобные экстремальные задачи, когда значения
функции известны (точно или с погрешностью) лишь на сетке. Кроме того
в этой главе предложен алгоритм для построения интерполяционного
параболического сплайна в случае, когда интерполируемая функция
y(x) задана на отрезке [a, b] неявным уравнением ![]()
Далее в этой главе демонстрировались возможности применения сплайнов для построения численных решений интегральных уравнений второго рода, краевых задач и задачи Коши для обыкновенных дифференциальных уравнений с помощью параболических и кубических сплайнов. При этом систематически использовались в качестве базисных функций B-сплайны. Идея использования B-сплайнов более высоких степеней в дальнейшем активно использовалась Де Буром. Выше уже отмечались трудности применения сплайнов при численном решении задачи Коши. В дальнейшем И.А. Пахнутов [29] широко использовал для этих целей сплайны с дополнительными узлами, введенные в [28]. Выбирая специальным образом дополнительные узлы, ему удалось построить устойчивые методы приближенного решения задач Коши.
В главе "Эрмитовы сплайны и нелинейные приближения" впервые
рассматриваются аналоги эрмитовых сплайнов в случае, когда сплайн
склеивается из полиномов четной степени. Приводятся оценки погрешности
аппроксимации. В этой же главе изучалась погрешность аппроксимации
эрмитовыми сплайнами нечетной степени с n нефиксированными узлами.
Используя результаты В.Л. Великина [22], см. также [26],
соответствующее утверждение можно записать в точной форме:
если ![]() то существует сетка
то существует сетка
![]() что для эрмитового
интерполяционного сплайна
что для эрмитового
интерполяционного сплайна ![]() выполняется
неравенство
выполняется
неравенство 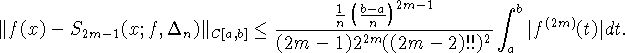
Здесь важно отметить, что в оценке погрешности отражена зависимость
как от числа узлов n, так и от степени 2m-1 эрмитового сплайна.
Приведены численные алгоритмы для нахождения узлов сетки ![]()
Поступила 7.09.96
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ