Обозначим через 
множество
функций 
определенных, дважды дифференцируемых на
вторая производная 
которых локально
абсолютно непрерывна, а 
Известно (см.,
например, [2]), что если 
то 
и
принадлежат 
Для функции 
рассмотрим во множестве W следующую
задачу
Лемма 1.
Для любой функции задача
(3.1)-(3.3) имеет, и причем единственное, решение.
Д о к а з а т е л ь с т в о. Найдем частное
решение уравнения (3.1), удовлетворяющее условию (3.2). Положим
и применим оператор Фурье
к уравнению (3.1). Воспользовавшись свойством [6]
получим для 
уравнение
Отсюда находим
Эта функция, очевидно, принадлежит 
Поэтому функция
также будет принадлежать Нетрудно
убедиться, что на всей оси и, в частности, на полуоси 
функция 
удовлетворяет уравнению (3.1). По предположению
функция f на полуоси вещественная, поэтому
вещественная функция 
удовлетворяет уравнению
(3.1) и условию (3.2).
Рассмотрим характеристическое уравнение
дифференциального оператора 
Корнями
этого уравнения являются числа
Поэтому общее решение однородного уравнения 
имеет вид
Если выполнено условие (3.2), то 
и, следовательно,
Итак, общее решение задачи (3.1)-(3.2) имеет вид
За счет выбора константы C можно удовлетворить условию (3.3). В
результате мы получим решение задачи (3.1)-(3.3).
Докажем единственность решения. Пусть 
два
решения задачи (3.1)-(3.3). Тогда 
есть
решение однородной задачи
Мы уже знаем, что решение уравнения (3.6) с учетом условия (3.7)
имеет вид (3.5). Условие (3.8) влечет, что 
Следовательно, решение задачи (3.1)-(3.3) существует и
единственно для любой функции 
Лемма 1 доказана.
Лемма 2.
Норма опертора T, определяемого
формулой 
где 
решение задачи (3.1)-(3.3), в
пространстве 
равна 
Д о к а з а т е л ь с т в о. Для доказательства этого и следующего утверждения будут использоваться соображения Г. Харди, Дж. Литтльвуда, Г. Полиа [5], которые в дальнейшем развивались А.П. Буслаевым [2].
Рассмотрим следующий функционал
на множестве 
функций 
с условием 
Выберем наибольшее значение 
при котором этот функционал
неотрицателен. Для этого определим на W неотрицательный
функционал
при произвольных пока параметрах A и B. В результате
преобразования получаем
где
здесь мы использовали обозначения 
Окончательно имеем
где
Рассмотрим теперь функционал K на множестве функций с
условием При этом предположении
Наложим на параметры A и B условия
Тогда имеем
Потребуем, чтобы 
Тогда, если B>0, то
В результате имеем систему
Решая эту систему, получим, что
Таким образом, если 
то 
для
то есть
что можно записать в виде
Следовательно,
Убедимся, что на самом деле
Для этого достаточно доказать, что существует функция на которой (3.13) обращается в равенство. Из доказательства
(3.13) видно, что такая функция является решением задачи
Рассмотрим соответствующее характеристическое уравнение
Покажем, что у всех трех корней 
этого уравнения
вещественная часть отрицательная: 
Кубическое
уравнение всегда имеет хотя бы один действительный корень. Так
как функция 
монотонно возрастает, поскольку ее производная 
строго положительна, то
этот корень единствен. Легко заметить, что он отрицателен.
Итак, 
Корни 
и 
будут комплексно
сопряжены. Запишем их в виде 
и подставим это
выражение в (3.17). Получаем
Выделив действительную и мнимую часть, перепишем это уравнение в
виде системы
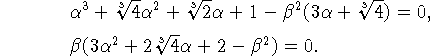
Она распадается на две системы уравнений относительно 
и 
Первая имеет вид
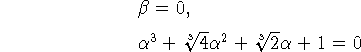
и дает первый корень 
Рассмотрим вторую систему
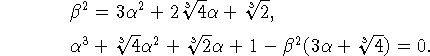
Из этой системы имеем следующее уравнение относительно
Как и выше, легко убедиться в том, что это уравнение имеет ровно
один действительный корень 
Таким образом, общее решение уравнения (3.14) имеет вид
где 
Убедимся, что полином 
в точке 
отличен от нуля.
Действительно, легко проверить, что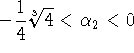 
и, кроме того, 
в
точках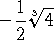 
и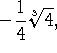 
а отсюда следует, что 
Используя
условия (3.15)-(3.16), находим, что свободные переменные 
и
выражаются через 
по формулам
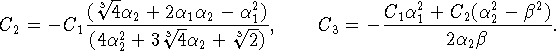
Лемма 2 доказана.
В следующей лемме будет вычислена величина
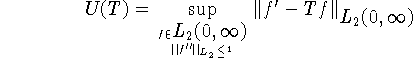
для оператора T, определенного на формулой
где решение задачи (3.1)-(3.3).
Лемма 3.
Имеет место равенство
Д о к а з а т е л ь с т в о. В силу
определения оператора T
Для доказательства (3.18) достаточно доказать неравенство
на множестве функций с условием 
и
показать, что оно точное. Обозначим 
Тогда неравенство (3.19) и условие
примут соответственно вид
Таким образом, мы должны доказать, что на множестве 
функций
с условием (3.21) функционал
неотрицателен и существует функция 
на которой (3.22)
обращается в равенство.
Так же как при доказательстве леммы 2 убеждаемся, что функционал
и функционал
при выполнении условий
связаны на равенством
где 
Условия 
и A>0 обеспечивают
неотрицательность функционала 
так как в этом случае
Решая систему
получаем значения 
Таким образом, если 
то 
для 
и, как следствие, выполняется
неравенство (3.19). Отсюда следует оценка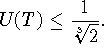 
Убедимся, что на самом деле имеет место равенство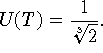 
Для этого достаточно доказать, что существует
функция на которой (3.19) обращается в равенство. Из
доказательства (3.19) видно, что для такой функции 
ее вторая
производная 
является решением задачи
Нетрудно заметить, что корни характеристического уравнения
для дифференциального уравнения (3.22) выражаются через корни
уравнения (3.17) следующим образом
Отсюда следует, что один из корней 
вещественный и
отрицательный, а два других (комплексно сопряженных) корня имеют
отрицательную вещественную часть. Доказательство леммы 3
завершается по той же схеме, что и доказательство леммы 2. Лемма 3
доказана.
Известен результат С.Б. Стечкина [1] для задачи (1.1)
В данном случае 
и потому для задачи
(1.2) имеет место формула
Из лемм 2 и 3 следует, что
Поэтому можно утверждать, что
и, следовательно,
Из неравенств (2.2) и (3.29) следует утверждение основной теоремы.
Поступила 1.09.94
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ