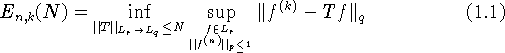
оператора дифференцирования порядка k на классе
n раз дифференцируемых функций
В 1967 г. С.Б. Стечкин [1] поставил и
начал изучать задачу о наилучшем приближении неограниченного
линейного оператора ограниченными операторами на некотором классе
элементов. В частности, он изучал задачу о наилучшем приближении
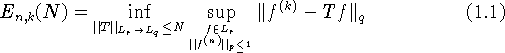
оператора дифференцирования порядка k на классе
![]()
n раз дифференцируемых функций ![]() на оси и полуоси.
на оси и полуоси.
В работах С.Б. Стечкина, В.В. Арестова, Л.В. Тайкова, Ю.Н. Субботина, В.Н. Габушина, В.И. Бердышева, А.П. Буслаева и др. (см. библиографию в [2-4]) дано решение задачи (1.1) для конкретных значений параметров.
В данной работе исследуется задача о наилучшем приближении
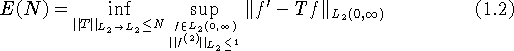
оператора дифференцирования первого порядка в пространстве
![]() на классе дважды дифференцируемых функций
(точнее, на классе функций
на классе дважды дифференцируемых функций
(точнее, на классе функций ![]() определенных,
дифференцируемых на
определенных,
дифференцируемых на ![]() производная f' которых
локально абсолютно непрерывна, а
производная f' которых
локально абсолютно непрерывна, а ![]() и
и
![]()
Основная теорема. При любом N>0 справедливы неравенства
![]()