2. Локально f-упорядоченные графы и их свойства

Введем следующее отношение линейного порядка на семействе всех подмножеств из V.

1. Если то считаем

2. Если где и числа, упорядоченные по возрастанию, то если или и для

3. Если | X | < | Y | и при то полагаем

Положим если и Для любого натурального числа s отношение можно продолжить на Если то если или и для некоторого

Пусть - множество всех помеченных простых графов порядка n и пусть F - множество всех функций вида и Тогда через обозначаем множество всех из таких, что и для любого Будем считать, что Через обозначаем множество меток Пусть , множество всех пар из таких, что и обозначает - множество всех пар из таких, что и Ясно, что из следует

Для введем обозначение

и

О п р е д е л е н и е 3. Пусть Простой помеченный граф H порядка n будем называть локально f-упорядоченным графом, если выполняются следующие условия :

для каждой метки графа H.

(2) Не существует помеченного простого графа B, изоморфного графу H, такого, что для B выполняется условие (1) настоящего определения и

Заметим, что термин ``локально'' используется во многих разных смыслах, в настоящей работе термин ``локально f-упорядоченный'' введен в силу того, что граф упорядочивается с помощью окрестностей его вершин.

Отметим также, что не для всех функций существует локально f-упорядоченный граф. Например, легко проверить, что для функции

не существует локально f-упорядоченного графа.

Далее нам понадобятся следующие функции.

(d(G,v,e) - есть валентность вершины с меткой v в графе G).

Пусть G - простой помеченный граф. Через обозначим множество всех помеченных графов вида где Ясно, что Через обозначим множество всех функций таких, что если и то для графа выполняется для любого Например,

Обозначим через - множество всех функций для которых выполняется условие: для любых Очевидно, что если где , тогда Через обозначим множество всех функций f из таких, что если и

где то для графа выполняются



где

Через обозначим множество всех функций таких, что для любых простых помеченных графов B,H из выполняется условие где Например,

По определению В общем случае, Обозначим через  - множество всех функций вида

Предложение 1. Пусть G - простой помеченный граф порядка n, и пусть функция Тогда существует локально f-упорядоченный граф, изоморфный графу G.

Д о к а з а т е л ь с т в о. Выберем из все графы H, для которых выполняется включение для любого l из множество выбранных графов. Из имеем, что

Введем в частичный порядок, считая если Понятно, что минимальные относительно порядка элементы из являются локально f-упорядоченными графами, изоморфными графу G. Предложение 1 доказано. Заметим, во-первых, что доказательства предложения конструктивно, т.е. позволяет находить для произвольного простого помеченного графа G локально f-упорядоченные графы, при

Во-вторых, что в общем случае из не следует равенство Например, для и графа G, заданного матрицей смежности A(G):

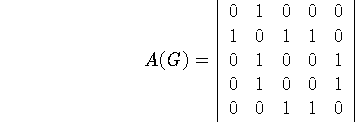
имеем, что так как (5, e) не принадлежит

Отметим также, что для любых имеет место одно из трех соотношений:

Предложение 2. Пусть G - простой помеченный граф и пусть функция f принадлежит . Тогда для того, чтобы функция f принадлежала достаточно, чтобы существовали функции из такие, что для любого графа H, изоморфного G, для любых из и v из V выполнялось условие

Д о к а з а т е л ь с т в о. Пусть H - простой помеченный граф, изоморфный G, функция f из и для любых из и v из V выполнено (2.1) для и Выберем произвольную пару из т.е.

при Из (2.1) имеем, что для любой перестановки из и любой пары выполняется условие

при где

Заметим, во-первых, что функции не зависят от v и и Во-вторых, так как из то и когда пробегает всю группу то пробегает тоже всю группу В-третьих, из условия следует, что Следовательно,

при условии т.е. имеет место включение

Напомним, что если - вершина графа G, т.е.  - метка вершины в графе G и  - метка этой же вершины в графе то Из определения и (2.2) получаем, что

для любой .

Предложение 2 доказано.

Следствие 1. Пусть G - простой помеченный граф и пусть функция f принадлежит . Тогда для того, чтобы функция f принадлежала достаточно, чтобы для любого графа H, изоморфного G и для любых из и v из V выполнялось условие

Через обозначаем множество графов

Следствие 2. Пусть f из и пусть H, B  - простые помеченные графы из такие, что и Тогда справедливо включение

Предложение 3. Пусть f из F и пусть  - простые помеченные графы из такие, что и l из и пусть существуют функции из такие, что для графов H и для любых из и v из выполняется условие  Тогда справедливы следующие утверждения:

Д о к а з а т е л ь с т в о. Возьмем пару из т.е.

при

Из (2.1) имеем, что для из и пары выполняется условие

при где

Заметим, во-первых, что функции не зависят от v и и Во-вторых, так как из то и и когда пробегает всю группу то пробегает тоже всю группу В-третьих, из условия следует, что Следовательно,

при условии т.е. имеет место включение

где т.е.

Из определения и (2.5) получаем, что

для ,

Покажем обратное включение.

Из (2.1 ) имеем, что

где

Возьмем пару из Из (2.6) получаем, что для из и пары выполняется условие

при условии где Следовательно,

при условии т.е. имеет место включение

где

Из определения и (2.7) получаем, что

для ,

Предложение 3 доказано.

Для краткости записи введем следующее

Условие 1. Пусть существуют функции из такие, что для графов H и для любых из и v из выполняется условие 

Предложение 4. Пусть G - простой помеченный граф и пусть функция f принадлежит Тогда существуют функции из такие, что для любого графа H, изоморфного G, для любых из и v из V, из включения следует справедливость условия 

Д о к а з а т е л ь с т в о. Пусть функция f принадлежит множеству тогда т.е. для любой пары из найдется такая пара из что графы равны. Ясно, что

Учитывая, что и получаем Теперь заменим на где Ясно, что Понятно, что выражение при зависит от графа H u Следовательно, существуют такие функции из что для любого из и выполняется условие

если Предложение 4 доказано.

Предложение 5. Пусть G - простой помеченный граф и пусть функция f принадлежит . Тогда для того, чтобы функция f принадлежала достаточно, чтобы для любого графа H, изоморфного G и для любых из и v из V выполнялось условие  при

Д о к а з а т е л ь с т в о. Пусть H - простой помеченный граф, изоморфный G и пусть пара из такая, что

где тогда для графа имеем, что Применяя равенство получаем, что

где

Напомним, что Из условия (2.1), учитывая, что и полагая имеем

Так как и то из выражение (2.8) получаем, что

Следовательно, Предложение 5 доказано.

Предложение 6. Пусть G - простой помеченный граф. Тогда

Д о к а з а т е л ь с т в о. Из определения функции следует, что для любых из и любого графа H из выполняется

Поэтому

Из следствия 1 имеем Теперь Применяя предложение 5, получаем Предложение 6 доказано.

Предложение 7. Пусть изоморфные (в частности, равные) простые графы порядка  - помеченный граф, полученный из с помощью меток из Если  - локально f-упорядоченные графы, то

Д о к а з а т е л ь с т в о. Из условий предложения следует, что Так как  - локально f-упорядоченный граф, то но  - локально f-упорядоченный граф, то Следовательно,
Предложение доказано.

Предложение 8. Пусть  - простые абстрактные графы порядка n.  - помеченный граф, полученный из с помощью меток из Если  - локально f-упорядоченные графы и то
и графы изоморфны.}

Следствие 3. Матрица смежности локально f-упорядоченного графа является полным инвариантом, т.е. она инвариантна относительно изоморфизмов графов.

О п р е д е л е н и е 4. Если то локально f-упорядоченный граф будем называть минимально упорядоченным графом.

Пусть граф Y из тогда обозначим через

Полагаем

Предложение 9. Пусть H - простой помеченный граф из Тогда для того чтобы H был минимально упорядоченным графом необходимо и достаточно, чтобы для любого графа B из выполнялось условие:

Д о к а з а т е л ь с т в о. Необходимость. От противного. Пусть H  - минимально упорядоченный граф, изоморфный графу G, т.е. и существует такой граф B из что

Тогда ясно, что Противоречие. Необходимость доказана.

Пусть для графа H и для каждого графа B из выполняется условие (2.9). Тогда для имеем, что и Предложение 9. доказано.

Предложение 10. Если f из то помеченный полный граф G конечного порядка является локально f-упорядоченный графом.

Предложение 11. Пусть f из Тогда для того, чтобы локально f-упорядоченный граф H, изоморфный G, был минимально упорядоченным достаточно, чтобы для любого графа B из выполнялось

Д о к а з а т е л ь с т в о. Пусть H  - локально f-упорядоченный граф и для любого графа B из выполняется (2.11), тогда из следует

Применяя условие (2.11) имеем, что

Из предложения 9. получаем, что H  - минимально упорядоченный граф. Предложение 11. доказано.

Заметим, что функция f из F, для которой для любых при n > 1 не является константой и принадлежит Для того чтобы построить для любого простого помеченного графа G изоморфный локально f-упорядоченный граф необходимо проанализировать систему уравнений с перестановками.