Сравнение разных способов оформления математических выражений конвертором LaTeX2HTML.

Существует несколько способов представления математических выражений конвертором на HTML-страничках:

Способы представления математических выражений конвертором в HTML 3.2.

N способа	Способы представления математических выражений	Ключи в .latex2html-init
1	"GIF-образ всего выражения": вся формула -один GIF-образ	$NO_SIMPLE_MATH = 1; $HTML_VERSION = '3.2';
2	"Простая математика": текстовое соответствие в сочетании с образами подвыражений	$NO_SIMPLE_MATH = 1; $HTML_VERSION = '3.2, math';

Способы представления влияют на:

1. Количество генерируемых GIF-образов $\Longrightarrow$ время работы конвертора.
2. Размер GIF-образов $\Longrightarrow$ общий размер конвертируемой статьи.
3. Степень "читаемости" сложных математических текстов с экрана.

На качество GIF-образов, созданных конвертором влияют:

• Правильный подбор параметров конфигурационного файла
  MATH_SCALE_FACTOR,DISP_SCALE_FACTOR. Эти параметры определяют размер GIF-образов, представляющих математические выражения в LaTeX-процедурах math, displaymath, equation.
• Использование эффекта "antialias"в сочетании с параметром SCALABLE_FONTS для сглаживания GIF-образов. Рисунки, графики, таблицы лучше конвертировать с установленным параметром ANTIALIAS=1. Использование этого параметра (ANTIALIAS_TEXT=1) при построении GIF-образов математических выражений приводит к увеличению размера GIF-образов и, следовательно, к увеличению времени конвертирования и загрузки. Восприятие формул с экрана с этим эффектом и без него индивидуально и зависит от конкретной статьи.

  Можно настраивать каждый конкретный образ, используя команду
  \htmlimage{antialias}
  внутри окружения eqnarray или equation (или другие команды по изменению образа).

• Установка параметра EXTRA_IMAGE_SCALE. Разработчики конвертора рекомендуют установить этот параметр равным 1.5 - 2 для улучшения качества математических формул при печати HTML-страниц.

Некоторые недостатки конвертирования математических выражений, влияющие на восприятие информации с экрана:

• Разброс внутристрочных формул (представленных GIF-образами) относительно текста.
• При выборе 3 способа конвертирования ("Простая математика") в выражении могут встретиться разные отражения одного и того же математического символа.

Ниже приведены небольшие примеры

Все выражение - образ с "noantialias":

$$\begin{eqnarray} (f,g)=\int\limits_{{R}^{m}}f(x){\bar g}(x)\,dx\,, \quad \Vert f\Vert=\sqrt{(f,f)} \end{eqnarray}$$

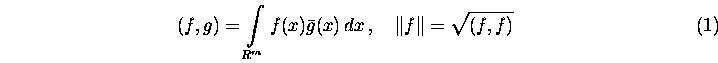
Все выражение - образ c "antialias":

$$\begin{eqnarray} (f,g)=\int\limits_{{R}^{m}}f(x){\bar g}(x)\,dx\,, \quad \Vert f\Vert=\sqrt{(f,f)} \end{eqnarray}$$

Текстовое соответствие, где возможно - иначе, образы подвыражений c "antialias":
В примерах ниже использование "antialias" позволяет увидеть, где в выражении текстовое изображение математических символов, а где - образ.

окружение "equation":

$$\int\limits_{{R}^{m}}^{} \bar{g} \sqrt{(f,f)}$$ (1)

Есть конструкции, где способ "Простая математика", не дает значительного выигрыша.

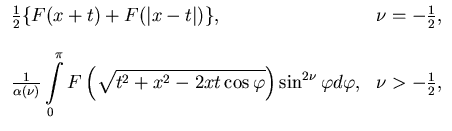
$$\left\{\vphantom{\begin{array}{ll} \frac{1}{2}\{F(x+t)+F(\vert x-... ...phi}\right)\sin^{2\nu}\varphi d\varphi, & \nu>-\frac{1}{2}, \end{array}}\right. \begin{array}{ll} \frac{1}{2}\{F(x+t)+F(\vert x-t\vert)\}, & \nu=... ...\cos\varphi}\right)\sin^{2\nu}\varphi d\varphi, & \nu>-\frac{1}{2}, \end{array}$$ (2)