

Next: 3 What algorithms are
Up: guide
Previous: 1 Tutorial
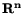
- is the space of n-dimensional vectors
x = (x1,..., xn)';
-
C[-
 , 0]
, 0]
- is the space of n-dimensional continuous on [-
 , 0]
functions q( . ) with the norm
| q( . )|C =
, 0]
functions q( . ) with the norm
| q( . )|C = 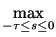 | q(s)|;
| q(s)|;
-
Q[-
 , 0]
, 0]
- is the space of n-dimensional functions q( . )
continuous everywhere on [-
 , 0] except, perhaps, a finite
set of points of discontinuity of the first kind
(at which q( . ) is continuous on the right),
with the norm
| q( . )|Q =
, 0] except, perhaps, a finite
set of points of discontinuity of the first kind
(at which q( . ) is continuous on the right),
with the norm
| q( . )|Q = 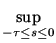 | q(s)|;
| q(s)|;
-
Q[-
 , 0)
, 0)
- is the restriction of the space
Q[-
 , 0]
on the half-interval [-
, 0]
on the half-interval [-  , 0), i.e.
Q[-
, 0), i.e.
Q[-  , 0) consists of n-dimensional functions
y(s),
-
, 0) consists of n-dimensional functions
y(s),
- 
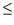 s < 0, with the properties:
s < 0, with the properties:
- 1)
- y( . ) is continuous on the half-interval [-
 , 0)
except, perhaps, a finite set of points of discontinuity
of the first kind
(at which q( . ) is continuous on the right);
, 0)
except, perhaps, a finite set of points of discontinuity
of the first kind
(at which q( . ) is continuous on the right);
- 2)
- y( . ) is bounded on [-
 , 0);
, 0);
- 3)
- there exists finite left-side limit at zero
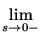 y(s);
y(s);
(the norm in
Q[-  , 0) is defined as
| y( . )|
, 0) is defined as
| y( . )|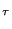 =
= 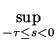 | y(s)|);
| y(s)|);
-
H =
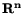 ×Q[-
×Q[-  , 0)
, 0)
- is the space of pairs
h = {x, y( . )} with the norm
| h|H = max { | x|,| y( . )|
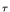 }.
}.
We denote by prime ' the transposition of vectors or
matrices.
The scalar product of vectors x,
y 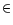
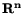 is
x'y, and the corresponding norm is defined by the
formula
| x| =
is
x'y, and the corresponding norm is defined by the
formula
| x| = 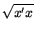 .
.
Remark 2.1.
It is necessary to note, the spaces H and
Q[-  , 0] are
isometric and the corresponding isometric mapping
, 0] are
isometric and the corresponding isometric mapping
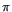 : Q[-
: Q[-  , 0]
, 0] H transfers functions
q( . )
H transfers functions
q( . )  Q[-
Q[-  , 0]
into pairs
{q(0);q(s),
, 0]
into pairs
{q(0);q(s),
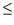 s < 0}
s < 0} 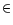 H.
So sometimes we will use the term "function" and for pairs
{x, y( . )}
H.
So sometimes we will use the term "function" and for pairs
{x, y( . )} 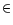 H.
We use the presentation of the space
Q[-
H.
We use the presentation of the space
Q[-  , 0] in the form
H =
, 0] in the form
H = 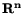 ×Q[-
×Q[-  , 0) because in case of
delay differential equations the point q(0) and the
points
{q(s),
, 0) because in case of
delay differential equations the point q(0) and the
points
{q(s),
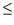 s < 0} (for
q( . )
s < 0} (for
q( . ) 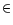 Q[-
Q[-  , 0]) play, generally speaking, different roles.
So it is convenient to use different notation for
the point q(0) and points
{q(s),
, 0]) play, generally speaking, different roles.
So it is convenient to use different notation for
the point q(0) and points
{q(s),
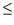 s < 0}
of the function
q( . )
s < 0}
of the function
q( . ) 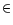 Q[-
Q[-  , 0]; for example:
x = q(0) and
y( . ) = {q(s),
, 0]; for example:
x = q(0) and
y( . ) = {q(s),
 s < 0},
and moreover to consider x and y( . ) as independent.
s < 0},
and moreover to consider x and y( . ) as independent.

The term basic functions is used for the subset of
C[-  , 0] which consists of elementary functions,
i.e. polynomials, trigonometrical functions, logarithms,
exponential.
, 0] which consists of elementary functions,
i.e. polynomials, trigonometrical functions, logarithms,
exponential.
- ARE
- - Algebraic Riccati Equation;
- DDE
- - Delay Differential Equations, also called
systems with delays, hereditary systems,
functional differential equations;
- ES-LQR
- - Explicit Solution of Linear Quadratic Regulator
(problem);
- GRE
- - Generalized Riccati Equations;
- LTI
- - Linear Time Invariant (system);
- MIMO
- - Multi Input - Multi Output;
- ODE
- - Ordinary Differential Equations.


Next: 3 What algorithms are
Up: guide
Previous: 1 Tutorial
 , 0)
except, perhaps, a finite set of points of discontinuity
of the first kind
(at which q( . ) is continuous on the right);
, 0)
except, perhaps, a finite set of points of discontinuity
of the first kind
(at which q( . ) is continuous on the right);
 , 0);
, 0);
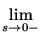 y(s);
y(s);