
КАБАНОВ Владислав ВладимировичНЕКОТОРЫЕ АЛГЕБРАИЧЕСКИЕ АСПЕКТЫ
ТЕОРИИ КОНЕЧНЫХ ГРАФОВ
Работа выполнена в отделе алгебры и топологии Института математики и
механики УрО РАН.
Научный консультант:
доктор физ.-мат. наук, профессор МАХНЕВ А.А.

Пусть ![]() группа подстановок на конечном множестве
группа подстановок на конечном множестве ![]() и
и ![]() связный граф с множеством вершин
связный граф с множеством вершин ![]() . Все графы, которые мы
будем рассматривать, являются неориентированными графами без петель и
кратных ребер, а в качестве подграфов мы рассматриваем только порожденные
подграфы. Говорят, что
. Все графы, которые мы
будем рассматривать, являются неориентированными графами без петель и
кратных ребер, а в качестве подграфов мы рассматриваем только порожденные
подграфы. Говорят, что ![]() дистанционно-транзитивна на графе
дистанционно-транзитивна на графе ![]() , если
для любого
, если
для любого
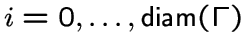 группа
группа ![]() действует
транзитивно на множестве упорядоченных пар вершин находящихся в
графе
действует
транзитивно на множестве упорядоченных пар вершин находящихся в
графе ![]() на расстоянии
на расстоянии ![]() друг от друга. Граф
друг от друга. Граф ![]() называется
дистанционно-транзитивным, если его группа автоморфизмов
называется
дистанционно-транзитивным, если его группа автоморфизмов
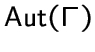 действует дистанционно-транзитивно на
действует дистанционно-транзитивно на ![]() .
Точное подстановочное представление группы
.
Точное подстановочное представление группы ![]()
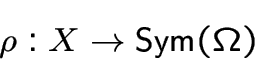
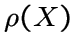 действует
дистанционно-транзитивно на некотором связном графе с множеством вершин
действует
дистанционно-транзитивно на некотором связном графе с множеством вершин
С другой стороны, как отмечают в своей монографии Э. Баннаи и Т. Ито, дистанционно-транзитивные графы можно рассматривать как "намного более общие структуры, чем конечные группы". Более того, некоторые теоретико-групповые построения допускают обобщение на дистанционно-транзитивные графы.
Дистанционно-транзитивные графы естественным образом обладают свойствами комбинаторной симметричности. Однако комбинаторная симметрия чаще всего не влечет дистанционной транзитивности графа. Наименьшим примером такого рода является граф Шрикханде, который является дистанционно-регулярным графом, но не является дистанционно-транзитивным. В настоящей диссертационной работе рассматриваются некоторые условия комбинаторной симметрии графа, которые влекут его дистанционную транзитивность. Как правило в этих случаях удается найти полное описание, рассматриваемых объектов.
Первые результаты о графах с условиями комбинаторной симметрии
были получены в пятидесятых годах.
Пусть 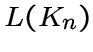 -- реберный граф полного графа
-- реберный граф полного графа ![]() или в других обозначениях треугольный граф
или в других обозначениях треугольный граф 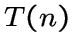 .
Этот граф является сильно регулярным графом с параметрами
.
Этот граф является сильно регулярным графом с параметрами
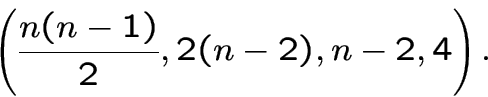
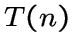 определяется однозначно своими параметрами для всех
определяется однозначно своими параметрами для всех 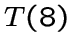 , такие же параметры имеют только три графа, которые были
найдены Л.С. Чангом в 1949 году [10].
, такие же параметры имеют только три графа, которые были
найдены Л.С. Чангом в 1949 году [10].
Реберный граф 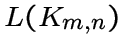 полного
многодольного графа
полного
многодольного графа ![]() (решетчатый
(решетчатый ![]() -граф)
является кореберно-регулярным
графом с параметрами
-граф)
является кореберно-регулярным
графом с параметрами
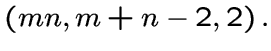 При
При ![]() решетчатый граф является сильно регулярным
графом с параметрами
решетчатый граф является сильно регулярным
графом с параметрами
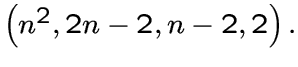 С.С. Шрикханде в [35] показал, что при
С.С. Шрикханде в [35] показал, что при ![]() граф
граф 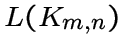 определяется этими параметрами, а при
определяется этими параметрами, а при ![]() ,
кроме
,
кроме 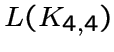 , существует еще в точности один граф, который теперь
называется графом Шрикханде.
Ситуацию без предположения о равенстве параметров
, существует еще в точности один граф, который теперь
называется графом Шрикханде.
Ситуацию без предположения о равенстве параметров ![]() и
и ![]() рассмотрели
независимо Дж.В. Мун [31] и А.Дж. Хоффман [22].
рассмотрели
независимо Дж.В. Мун [31] и А.Дж. Хоффман [22].
Матрица смежности графа ![]() -- это матрица
-- это матрица
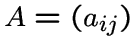 , строки и столбцы которой перенумерованы вершинами графа
, строки и столбцы которой перенумерованы вершинами графа
![]() , причем
, причем ![]() , если
, если ![]() является ребром в
является ребром в ![]() ,
,
![]() в противном случае.
Матрица смежности сильно регулярного графа
в противном случае.
Матрица смежности сильно регулярного графа ![]() с параметрами
с параметрами
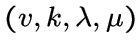 кроме собственного значения, равного
кроме собственного значения, равного ![]() , имеет
еще два действительных собственных значения разных знаков.
Если у сильно регулярного графа
, имеет
еще два действительных собственных значения разных знаков.
Если у сильно регулярного графа ![]() набор параметров
набор параметров
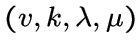 такой же,
как у треугольных или решетчатых
такой же,
как у треугольных или решетчатых ![]() -графов, то
отрицательное собственное значение его матрицы смежности равно
-графов, то
отрицательное собственное значение его матрицы смежности равно ![]() .
Это свойство дает возможность восстановить строение графа
.
Это свойство дает возможность восстановить строение графа ![]() с набором параметров, как у треугольных или решетчатых
с набором параметров, как у треугольных или решетчатых ![]() -графов.
-графов.
Граф ![]() называется сильным, если для любой пары
называется сильным, если для любой пары ![]() его вершин
число общих смежных с ними вершин зависит только от того, является
его вершин
число общих смежных с ними вершин зависит только от того, является ![]() ребром или нет.
Результаты Л.С. Чанга, С.С. Шрикханде и А.Дж. Хоффмана
были объединены Дж.Дж. Зейделем [34], который определил все сильные
графы с наименьшим собственным значением
ребром или нет.
Результаты Л.С. Чанга, С.С. Шрикханде и А.Дж. Хоффмана
были объединены Дж.Дж. Зейделем [34], который определил все сильные
графы с наименьшим собственным значением ![]() . Дж.Дж. Зейдель
показал, что кроме треугольных графов
. Дж.Дж. Зейдель
показал, что кроме треугольных графов 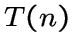 и решетчатых
и решетчатых ![]() -графов,
сильными графами, которые имеют наименьшее собственное значение
-графов,
сильными графами, которые имеют наименьшее собственное значение
![]() , являются только графы
, являются только графы ![]() , три графа Чанга,
графы Шрикханде, Шлефли, Клебша и Петерсена.
, три графа Чанга,
графы Шрикханде, Шлефли, Клебша и Петерсена.
Применяя метод С.С. Симса [36] перечисления 4-вершинных подграфов,
М.Д. Хестенс и Д.Г. Хигман в работе [19] показали,
что в сильно регулярных графах число 4-вершинных подграфов любого
заданного вида определяет число 4-вершинных подграфов всех других видов.
Это свойство позволило М.Д. Хестенсу и
Д.Г. Хигману получить более экономное доказательство теоремы
Дж.Дж. Зейделя для случая сильно регулярных графов.
Среди возможных 4-вершинных подграфов наиболее важную роль играют
подграфы, изоморфные ![]() (полный 4-вершинный граф),
(полный 4-вершинный граф), ![]() (полный 4-вершинный граф с удаленным ребром) и
(полный 4-вершинный граф с удаленным ребром) и ![]() (полный двудольный граф с долями из одной и трех вершин).
(полный двудольный граф с долями из одной и трех вершин).
Заметим, что если граф ![]() с наименьшим собственным значением, равным
с наименьшим собственным значением, равным
![]() , содержит 3-лапу
, содержит 3-лапу
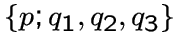 (4-вершинный подграф, изоморфный
(4-вершинный подграф, изоморфный ![]() ),
то любая вершина
),
то любая вершина
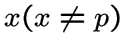 из
из ![]() , смежная с вершинами
, смежная с вершинами ![]() и
и ![]() , смежна с
, смежна с ![]() и не смежна с
и не смежна с ![]() .
.
Таким образом, граф с наименьшим собственным значением, равным
![]() , либо не содержит 3-лап, либо содержит 3-лапы, но тогда окрестность
любой его вершины не содержит 3-лап.
, либо не содержит 3-лап, либо содержит 3-лапы, но тогда окрестность
любой его вершины не содержит 3-лап.
Если ![]() пара вершин графа
пара вершин графа ![]() , которые находятся на расстоянии 2
друг от друга, то подграф на множестве общих смежных с ними вершин называется
, которые находятся на расстоянии 2
друг от друга, то подграф на множестве общих смежных с ними вершин называется
![]() -подграфом графа
-подграфом графа ![]() .
.
Графы без 3-лап с несвязными ![]() -подграфами
были изучены в 1994 году А.Е. Брауэром и М. Нуматой [7].
В графе с несвязными
-подграфами
были изучены в 1994 году А.Е. Брауэром и М. Нуматой [7].
В графе с несвязными ![]() -подграфами
любой подграф, изоморфный
-подграфами
любой подграф, изоморфный ![]() , содержится в подграфе, изоморфном
, содержится в подграфе, изоморфном
![]() , то есть в
, то есть в ![]() . Такие графы мы будем называть
. Такие графы мы будем называть
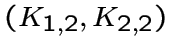 -однородными графами.
Таким образом, граф, у которого все
-однородными графами.
Таким образом, граф, у которого все ![]() -подграфы несвязны, является
-подграфы несвязны, является
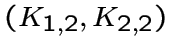 -однородным графом.
-однородным графом.
Следующая теорема, которая
обобщает теорему А.Е. Брауэра и М. Нуматы в том случае, когда граф
содержит ![]() -коклику, доказывается в первой главе диссертации [45].
Для того, чтобы сформулировать теорему, нам понадобится понятие
кликового расширения графа.
Кликовым расширением графа
-коклику, доказывается в первой главе диссертации [45].
Для того, чтобы сформулировать теорему, нам понадобится понятие
кликового расширения графа.
Кликовым расширением графа ![]() называется граф,
полученный заменой каждой вершины
называется граф,
полученный заменой каждой вершины ![]() из
из ![]() на полный
подграф
на полный
подграф 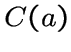 , содержащий не менее одной вершины, причем вершины
из различных клик
, содержащий не менее одной вершины, причем вершины
из различных клик 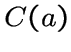 и
и 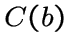 смежны тогда и только тогда,
когда вершины
смежны тогда и только тогда,
когда вершины ![]() и
и ![]() смежны в
смежны в ![]() .
Кликовое расширение графа
.
Кликовое расширение графа ![]() называется
называется
![]() -расширением
-расширением ![]() , если для любой вершины
, если для любой вершины ![]() подграф
подграф 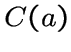 содержит
содержит ![]() вершин для некоторого фиксированного
вершин для некоторого фиксированного
![]() . Заметим, что если граф
. Заметим, что если граф ![]() не содержит 3-лап, то и
любое его кликовое расширение не содержит 3-лап.
не содержит 3-лап, то и
любое его кликовое расширение не содержит 3-лап.
ТЕОРЕМА 1.
Пусть связный граф ![]() содержит
содержит ![]() -коклику и не содержит
-коклику и не содержит ![]() -лап.
Если любой подграф из
-лап.
Если любой подграф из ![]() , изоморфный
, изоморфный ![]() , содержится в подграфе,
изоморфном
, содержится в подграфе,
изоморфном ![]() , то
, то
![]() является кликовым расширением одного из следующих графов:
является кликовым расширением одного из следующих графов:
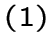 решетчатый
решетчатый ![]() -граф при
-граф при ![]() ,
, ![]() ;
;
 треугольный граф
треугольный граф 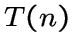 при
при ![]() ;
;
 граф Шлефли.
граф Шлефли.
В работе [29] М. Нуматой была получена
классификация реберно-регулярных графов,
которые не содержат 3-лап и содержат ![]() -коклику.
-коклику.
Следующая теорема является аналогом этого результата для кореберно-регулярных графов без 3-лап и также доказывается в первой главе диссертации [55].
ТЕОРЕМА 2.
Пусть ![]() -- кореберно-регулярный граф без
-- кореберно-регулярный граф без ![]() -лап.
Тогда
-лап.
Тогда ![]() является либо дополнительным графом к регулярному графу
без треугольников, либо
является либо дополнительным графом к регулярному графу
без треугольников, либо ![]() -расширением
-расширением
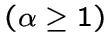 одного из
следующих графов:
одного из
следующих графов:
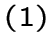 вполне несвязный граф с числом вершин
вполне несвязный граф с числом вершин ![]()
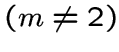 ;
;
 решетчатый
решетчатый ![]() -граф при
-граф при
![]() ;
;
 треугольный граф
треугольный граф 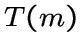 при
при ![]() ;
;
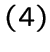 граф Шлефли.
граф Шлефли.
В той же работе [29] М. Нуматой получена классификация
реберно-регулярных графов диаметра не менее 3,
которые не содержат 3-лап и
содержат ![]() -коклику.
-коклику.
Полученные выше результаты служат основой для исследования графов без 3-лап с более слабыми условиями регулярности во второй главе диссертации.
Пусть ![]() пара вершин графа
пара вершин графа ![]() , которые находятся на расстоянии 2
друг от друга. Обозначим число вершин
, которые находятся на расстоянии 2
друг от друга. Обозначим число вершин ![]() -подграфа для
-подграфа для ![]() через
через
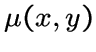 . Если все
. Если все ![]() -подграфы
графа
-подграфы
графа ![]() имеют одинаковое число вершин, то есть
имеют одинаковое число вершин, то есть 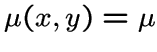 ,
то это число называется параметром
,
то это число называется параметром ![]() графа
графа ![]() .
Понятно, что если граф имеет параметр
.
Понятно, что если граф имеет параметр ![]() , то
, то ![]() не меньше 1.
Если граф
не меньше 1.
Если граф ![]() имеет параметр
имеет параметр ![]() , но его значение неизвестно,
то мы говорим, что
, но его значение неизвестно,
то мы говорим, что ![]() имеет равномощные
имеет равномощные ![]() -подграфы.
По определению сильного графа, любая пара несмежных вершин в нем имеет одно и
то же число общих соседей. Это условие автоматически приводит к тому, что
либо диаметр сильного графа равен 2 и он имеет равномощные
-подграфы.
По определению сильного графа, любая пара несмежных вершин в нем имеет одно и
то же число общих соседей. Это условие автоматически приводит к тому, что
либо диаметр сильного графа равен 2 и он имеет равномощные ![]() -подграфы,
либо число общих соседей любой пары несмежных вершин в нем равно 0.
Таким образом, условие равномощности
-подграфы,
либо число общих соседей любой пары несмежных вершин в нем равно 0.
Таким образом, условие равномощности ![]() -подграфов значительно
ослабляет соответствующее условие в определении сильного графа.
-подграфов значительно
ослабляет соответствующее условие в определении сильного графа.
Вторая глава диссертации посвящена классификации
графов без 3-лап с равномощными ![]() -подграфами без ограничения на диаметр
графа.
Изучение класса графов без 3-лап с
равномощными
-подграфами без ограничения на диаметр
графа.
Изучение класса графов без 3-лап с
равномощными ![]() -подграфами самая трудная и большая по объему часть работы.
Оказалось, что сильное влияние на
строение графа оказывает наличие или отсутствие в графе порожденных 4-циклов.
Графы без 4-циклов с равномощными
-подграфами самая трудная и большая по объему часть работы.
Оказалось, что сильное влияние на
строение графа оказывает наличие или отсутствие в графе порожденных 4-циклов.
Графы без 4-циклов с равномощными ![]() -подграфами изучал П. Тервиллигер
в [38]. Он доказал реберную регулярность таких графов при некоторых
дополнительных условиях, в частности, для регулярных графов диаметра 2.
Графы без порожденных 4-циклов с равномощными
-подграфами изучал П. Тервиллигер
в [38]. Он доказал реберную регулярность таких графов при некоторых
дополнительных условиях, в частности, для регулярных графов диаметра 2.
Графы без порожденных 4-циклов с равномощными ![]() -подграфами мы будем
называть графами Тервиллигера.
-подграфами мы будем
называть графами Тервиллигера.
Следующая теорема классифицирует регулярные графы Тервиллигера без 3-лап [56].
ТЕОРЕМА 3.
Связный регулярный граф Тервиллигера
без 3-лап является ![]() -расширением одного из следующих графов:
-расширением одного из следующих графов:
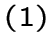 граф без
граф без ![]() -лап с
-лап с ![]() ,
,
 граф икосаэдра.
граф икосаэдра.
В следующей теореме классифицированы связные ![]() -регулярные
графы без 3-лап [56].
-регулярные
графы без 3-лап [56].
ТЕОРЕМА 4.
Связный ![]() -регулярный граф
-регулярный граф ![]() без
без
![]() -лап либо является графом Тервиллигера, либо имеет диаметр
-лап либо является графом Тервиллигера, либо имеет диаметр ![]() .
.
Теперь строение связных ![]() -регулярных графов определяют теоремы теорема 2
и теорема 3, поскольку в них определены графы Тервиллигера без
-регулярных графов определяют теоремы теорема 2
и теорема 3, поскольку в них определены графы Тервиллигера без ![]() -лап
и кореберно-регулярные графы без 3-лап.
-лап
и кореберно-регулярные графы без 3-лап.
В следующей теореме мы не предполагаем регулярности графа, и, таким образом,
она завершает классификацию графов Тервиллигера без 3-лап [57].
Эта теорема расширяет теорему Тэйлора-Левингстона [37].
Через ![]() обозначим порожденный подграф, состоящий из вершины
обозначим порожденный подграф, состоящий из вершины ![]() и всех смежных с ней вершин.
Через
и всех смежных с ней вершин.
Через ![]() обозначим подграф
обозначим подграф
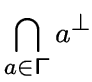 .
.
ТЕОРЕМА 5.
Пусть ![]() -- связный граф
Тервиллигера без
-- связный граф
Тервиллигера без ![]() -лап. Тогда либо граф
-лап. Тогда либо граф ![]() является
является
![]() -расширением графа икосаэдра, либо
подграф на множестве всех вершин с некликовыми окрестностями из
-расширением графа икосаэдра, либо
подграф на множестве всех вершин с некликовыми окрестностями из
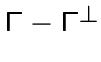 является пустым, кликой или
является пустым, кликой или ![]() -расширением связного
графа с
-расширением связного
графа с ![]() .
.
При условии, что граф содержит 3-коклику, удается получить полную
классификацию не только графов Тервиллигера без 3-лап, но и всех
графов без 3-лап с равномощными ![]() -подграфами [57].
-подграфами [57].
ТЕОРЕМА 6.Пусть ![]() -- связный граф без
-- связный граф без ![]() -лап,
содержащий
-лап,
содержащий ![]() -коклику. Пусть также все
-коклику. Пусть также все ![]() -подграфы из
-подграфы из ![]() имеют одинаковое число вершин.
Тогда либо
имеют одинаковое число вершин.
Тогда либо ![]() имеет диаметр больше двух и является графом
из заключения теоремы 5, либо граф
имеет диаметр больше двух и является графом
из заключения теоремы 5, либо граф ![]() является
регулярным графом и его строение определяют пункты (2), (3), (4)
теоремы 2.
является
регулярным графом и его строение определяют пункты (2), (3), (4)
теоремы 2.
Следующая теорема посвящена описанию графов
без 3-лап с регулярными ![]() -подграфами одинаковой ненулевой валентности.
Регулярный граф называется редуцированным,
если для любой вершины
-подграфами одинаковой ненулевой валентности.
Регулярный граф называется редуцированным,
если для любой вершины ![]() множество
множество
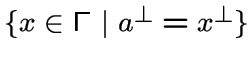 состоит из единственной вершины
состоит из единственной вершины ![]() .
В статье [27] А.А. Махнев перенес это понятие на класс всех графов.
Произвольный граф
.
В статье [27] А.А. Махнев перенес это понятие на класс всех графов.
Произвольный граф ![]() называется редуцированным,
если для любой вершины
называется редуцированным,
если для любой вершины ![]() множество
множество
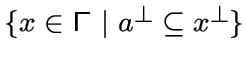 состоит из единственной вершины
состоит из единственной вершины ![]() .
Легко видеть, что в классе регулярных графов оба определения эквивалентны.
.
Легко видеть, что в классе регулярных графов оба определения эквивалентны.
В [27] А.А. Махнев классифицировал редуцированные графы без
3-лап с регулярными ![]() -подграфами валентности
-подграфами валентности ![]() , где
, где ![]() .
Мы докажем, что если
.
Мы докажем, что если ![]() является графом без 3-лап с регулярными
является графом без 3-лап с регулярными
![]() -подграфами одинаковой валентности
-подграфами одинаковой валентности ![]() , где
, где ![]() , и
для любой вершины
, и
для любой вершины ![]() из
из ![]() множество
множество
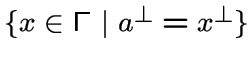 совпадает с
совпадает с
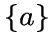 , то и множество
, то и множество
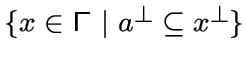 состоит из единственной вершины
состоит из единственной вершины ![]() . Следующая теорема [43,44]
усиливает основной результат из [27].
. Следующая теорема [43,44]
усиливает основной результат из [27].
ТЕОРЕМА 7.
Пусть ![]() -- связный граф, который
не содержит
-- связный граф, который
не содержит ![]() -лап и содержит
-лап и содержит ![]() -коклику и выполнены
следующие условия:
-коклику и выполнены
следующие условия:
![]() все
все ![]() -подграфы из
-подграфы из ![]() являются регулярными
графами одинаковой валентности
являются регулярными
графами одинаковой валентности ![]() для некоторого числа
для некоторого числа ![]() ;
;
![]() для любой вершины
для любой вершины ![]() множество
множество
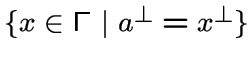 состоит из единственной вершины
состоит из единственной вершины ![]() .
.
Тогда граф ![]() является треугольным графом
является треугольным графом 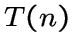 при
при ![]() ,
графом икосаэдра или графом Шлефли.
,
графом икосаэдра или графом Шлефли.
В работе [19] М.Д. Хестенс и Д.Г. Хигман отметили другой
момент, касающийся связи между теорией графов
и теорией транзитивных групп подстановок.
Пусть ![]() -- транзитивная группа подстановок на множестве
-- транзитивная группа подстановок на множестве ![]() .
Тогда орбиты группы
.
Тогда орбиты группы ![]() на множестве
на множестве
![]() называются орбиталами, а их число -- рангом группы
называются орбиталами, а их число -- рангом группы ![]() .
Каждый орбитал
.
Каждый орбитал ![]() является либо симметричным, либо строго
антисимметричным. В первом случае он
определяет обыкновенный граф с множеством вершин
является либо симметричным, либо строго
антисимметричным. В первом случае он
определяет обыкновенный граф с множеством вершин ![]() и множеством
ребер
и множеством
ребер ![]() . Во втором случае орбитал
имеет симметричную ему пару
. Во втором случае орбитал
имеет симметричную ему пару
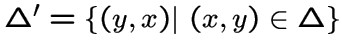 и
определяет ориентированный граф.
Известно, что группа
и
определяет ориентированный граф.
Известно, что группа ![]() обладает
симметричным орбиталом тогда и только тогда, когда ее порядок является
четным числом [40].
обладает
симметричным орбиталом тогда и только тогда, когда ее порядок является
четным числом [40].
Если группа ![]() имеет ранг 3, то оба орбитала, отличные от диагонали
имеет ранг 3, то оба орбитала, отличные от диагонали
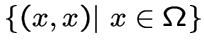 , являются симметричными и
определяют пару дополнительных сильно регулярных
графов. Такой сильно регулярный граф называется графом ранга 3.
В настоящее время с использованием классификации конечных простых групп
получено полное описание групп и графов ранга 3 ([9],
[25], [2], [26], [24]).
, являются симметричными и
определяют пару дополнительных сильно регулярных
графов. Такой сильно регулярный граф называется графом ранга 3.
В настоящее время с использованием классификации конечных простых групп
получено полное описание групп и графов ранга 3 ([9],
[25], [2], [26], [24]).
Много работ посвящено изучению транзитивных групп
подстановок без ограничений на их ранг и графов, которые определяются
их орбиталами.
В программном комплексе GAP [32] имеется специальная инструкция
EdgeOrbitGraph, которая позволяет строить граф по орбиталу заданной
транзитивной группы подстановок. При помощи этой
инструкции автором найден пример дистанционно-транзитивного
локально без 3-лап графа с несвязными окрестностями вершин.
Этот граф является локально 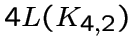 -графом,
то есть графом, любая окрестность вершины которого является
объединением четырех решетчатых
-графом,
то есть графом, любая окрестность вершины которого является
объединением четырех решетчатых ![]() -графов. Он
получается из наименьшего орбитала группы Хигмена-Симса при
представлении ее как транзитивной группы подстановок, действующей на классе
центральных инволюций.
-графов. Он
получается из наименьшего орбитала группы Хигмена-Симса при
представлении ее как транзитивной группы подстановок, действующей на классе
центральных инволюций.
С другой стороны, интересен следующий, связанный с данным, вопрос.
А именно, какими свойствами должен обладать граф, чтобы множество
его ребер оказалось орбиталом для группы подстановок, действующей
транзитивно на его вершинах (граф, изоморфный такому графу,
мы назовем орбитальным)?
Этот вопрос тесно связан с вопросом изучения групп автоморфизмов графов.
В работах [14], [15] Х. Еномото получил
характеризацию графов Хэмминга как орбитальных графов
для транзитивных групп подстановок с определенными ограничениями
на их подстепени.
Первая теорема третьей главы диссертации, опубликованная в [56],
усиливает результат Х. Еномото.
Для ее формулировки нам понадобится определение отделимого графа.
Граф ![]() назовем отделимым, если для любой вершины
назовем отделимым, если для любой вершины ![]() из
из
![]() подграф
подграф 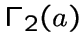 содержит вершины
содержит вершины ![]() на расстоянии 2 в
на расстоянии 2 в
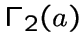 и
и ![]() -подграф
-подграф ![$[b]\cap [c]$](img95.gif) для любой такой пары
не пересекает
для любой такой пары
не пересекает ![]() .
.
ТЕОРЕМА 8.
Пусть ![]() -- связный вполне
регулярный граф
с параметрами
-- связный вполне
регулярный граф
с параметрами
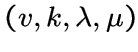 ,
, ![]() .
Граф
.
Граф ![]() отделим тогда и только тогда, когда
он является одним из следующих графов:
отделим тогда и только тогда, когда
он является одним из следующих графов:
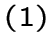 граф Хемминга
граф Хемминга 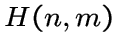 при
при
![]() ;
;
 треугольный граф
треугольный граф 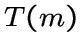 при
при ![]() ;
;
 граф Шлефли;
граф Шлефли;
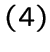 граф икосаэдра.
граф икосаэдра.
Используя классификацию реберно-регулярных
графов без 3-лап [29], М. Нумата в работе [30] получил
характеризацию
графов Грассмана и Джонсона как графов локально без 3-лап, в которых
все ![]() -подграфы являются изоморфными
реберно-регулярными графами
диаметра 2. Заметим, что если граф
-подграфы являются изоморфными
реберно-регулярными графами
диаметра 2. Заметим, что если граф ![]() удовлетворяет условию
теоремы М. Нуматы, то из последнего условия на все
удовлетворяет условию
теоремы М. Нуматы, то из последнего условия на все ![]() -подграфы
графа
-подграфы
графа ![]() непосредственно следует реберная регулярность самого
непосредственно следует реберная регулярность самого ![]() .
.
Наша следующая цель получить классификацию локально без 3-лап графов
с более слабым условием на ![]() -подграфы, которое не влечет
даже регулярности графа. Это стало возможно благодаря
классификации графов без 3-лап с равномощными
-подграфы, которое не влечет
даже регулярности графа. Это стало возможно благодаря
классификации графов без 3-лап с равномощными ![]() -подграфами.
С помощью этой классификации мы исследуем
класс графов, в которых окрестности вершин
не содержат 3-лап и все
-подграфами.
С помощью этой классификации мы исследуем
класс графов, в которых окрестности вершин
не содержат 3-лап и все ![]() -подграфы являются регулярными графами
валентности
-подграфы являются регулярными графами
валентности ![]() , где
, где ![]() .
В отличии от [30] мы не требуем даже равномощности всех
.
В отличии от [30] мы не требуем даже равномощности всех ![]() -подграфов.
Поскольку наше условие на
-подграфов.
Поскольку наше условие на ![]() -подграфы не влечет регулярности графа,
то мы дополнительно накладываем на граф условие редуцированности.
-подграфы не влечет регулярности графа,
то мы дополнительно накладываем на граф условие редуцированности.
ТЕОРЕМА 9.
Пусть ![]() -- связный граф, который
удовлетворяет следующим условиям:
-- связный граф, который
удовлетворяет следующим условиям:
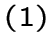 окрестность любой вершины из
окрестность любой вершины из ![]() не содержит
не содержит ![]() -лап;
-лап;

![]() содержит
содержит ![]() -лапу;
-лапу;
 все
все ![]() -подграфы из
-подграфы из ![]() являются регулярными
графами одинаковой валентности
являются регулярными
графами одинаковой валентности ![]() для некоторого числа
для некоторого числа ![]() ;
;
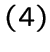 для любой вершины
для любой вершины ![]() множество
множество
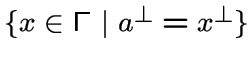 состоит из единственной вершины
состоит из единственной вершины ![]() .
Тогда
.
Тогда ![]() является локально
является локально ![]() -графом, где
-графом, где
![]() один из следующих графов:
один из следующих графов:
![]()
![]() -расширение решетчатого
-расширение решетчатого ![]() -графа
при
-графа
при
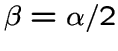 и
и ![]() ,
, ![]() ;
;
![]() треугольный граф
треугольный граф 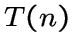 при
при ![]() ;
;
![]() граф Шлефли.
граф Шлефли.
Если граф ![]() является
является ![]() -расширением решетчатого
-расширением решетчатого ![]() -графа,
то класс локально
-графа,
то класс локально ![]() -графов довольно широк и труден
для изучения. Примерами таких графов являются графы Грассмана,
графы Джонсона и их частные.
-графов довольно широк и труден
для изучения. Примерами таких графов являются графы Грассмана,
графы Джонсона и их частные.
Пусть ![]() является
является ![]() -мерным векторным
пространством над конечным полем
-мерным векторным
пространством над конечным полем ![]() .
Графом Грассмана для
.
Графом Грассмана для ![]() -подпространств из
-подпространств из ![]() называется граф
называется граф
![$\left[V\atop m\right]$](img108.gif) с множеством вершин, равным
множеству всех подпространств размерности
с множеством вершин, равным
множеству всех подпространств размерности ![]() из
из ![]() , причем две вершины
, причем две вершины
![]() смежны тогда и только тогда, когда
смежны тогда и только тогда, когда
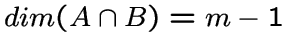 .
Если
.
Если ![]() -- конечное множество, то графом Джонсона для
-- конечное множество, то графом Джонсона для
![]() -подмножеств из
-подмножеств из ![]() называется граф с множеством вершин, равным
множеству
называется граф с множеством вершин, равным
множеству
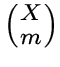 всех
всех ![]() -элементных подмножеств из
-элементных подмножеств из ![]() , причем две вершины
, причем две вершины ![]() смежны тогда и только тогда, когда
смежны тогда и только тогда, когда
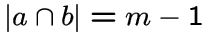 .
Если множество
.
Если множество ![]() состоит из
состоит из ![]() элементов, то такой граф
обозначим через
элементов, то такой граф
обозначим через 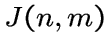 . Заметим, что граф
. Заметим, что граф 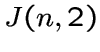 совпадает с
треугольным графом
совпадает с
треугольным графом 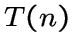 .
Пусть
.
Пусть ![]() -- некоторое разбиение множества вершин графа
-- некоторое разбиение множества вершин графа ![]() на подмножества. Частным
на подмножества. Частным
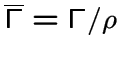 для графа
для графа ![]() по разбиению
по разбиению ![]() называется граф на фактор-множестве по
называется граф на фактор-множестве по ![]() множества вершин
множества вершин ![]() ,
в котором две вершины
,
в котором две вершины
![]() смежны только, если
смежны только, если
![]() и граф
и граф ![]() содержит ребро, которое соединяет
некоторую вершину из класса
содержит ребро, которое соединяет
некоторую вершину из класса ![]() с некоторой вершиной из класса
с некоторой вершиной из класса
![]() .
Пусть
.
Пусть ![]() и
и ![]() является разбиением множества вершин
графа Джонсона
является разбиением множества вершин
графа Джонсона 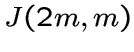 на двухэлементные классы, содержащие
на двухэлементные классы, содержащие
![]() -элементное подмножество и его дополнение в
-элементное подмножество и его дополнение в ![]() .
Частным графа Джонсона называется граф
.
Частным графа Джонсона называется граф 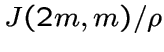 .
.
Графы Джонсона и частные графов Джонсона дают нам примеры локально
![]() -графов. Эти примеры не исчерпывают класс таких графов.
В статье [3] построены другие примеры локально
-графов. Эти примеры не исчерпывают класс таких графов.
В статье [3] построены другие примеры локально ![]() -графов
и найдены все локально
-графов
и найдены все локально ![]() -графы. Там же получено описание локально
-графы. Там же получено описание локально
![]() -графов, в которых
каждый
-графов, в которых
каждый ![]() -подграф является объединением изолированных четырехугольников.
Характеризация локально
-подграф является объединением изолированных четырехугольников.
Характеризация локально ![]() -графов при
-графов при ![]() получена Дж. Холлом в
[17]. Проблема полного описания локально
получена Дж. Холлом в
[17]. Проблема полного описания локально ![]() -графов
для любых
-графов
для любых ![]() остается открытой.
Мало пока известно в общем случае и о локально
треугольных графах.
остается открытой.
Мало пока известно в общем случае и о локально
треугольных графах.
Однако, если все ![]() -подграфы из
-подграфы из ![]() имеют диаметр 2, можно получить более точный ответ.
имеют диаметр 2, можно получить более точный ответ.
ТЕОРЕМА 10.
Пусть ![]() -- связный граф, который
удовлетворяет условиям теоремы 9 и
все
-- связный граф, который
удовлетворяет условиям теоремы 9 и
все ![]() -подграфы из
-подграфы из ![]() имеют диаметр 2.
Тогда
имеют диаметр 2.
Тогда ![]() является одним из следующих графов:
является одним из следующих графов:
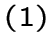 граф Грассмана;
граф Грассмана;
 граф Джонсона или его частное;
граф Джонсона или его частное;
 локально
локально 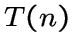 -граф при
-граф при ![]() ;
;
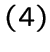 граф Госсета
граф Госсета 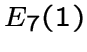 .
.
Все графы Грассмана, графы Джонсона и их частные, граф Госсета 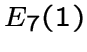 являются дистанционно-транзитивными графами.
являются дистанционно-транзитивными графами.
Заметим также, что граф системы корней ![]() (см. [5])
является локально
(см. [5])
является локально 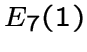 -графом и играет особую роль в теории графов,
у которых любое собственное значение не меньше, чем
-графом и играет особую роль в теории графов,
у которых любое собственное значение не меньше, чем ![]() .
По теореме А.Дж. Хоффмана [23] любой такой граф является либо
обобщенным реберным графом, либо подграфом
.
По теореме А.Дж. Хоффмана [23] любой такой граф является либо
обобщенным реберным графом, либо подграфом 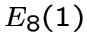 .
.
В последней главе диссертации изучаются некоторых теоретико-графовые свойства графов без 3-лап и их обобщений. В ней рассматривается, в частности, соотношение нижних параметров доминирования и неприводимости для графов без 3-лап и графов, все блоки которых не содержат 3-лап.
Результаты работы докладывались на Международных конференциях по алгебре в 1993 году в Красноярске [42], в 1996 году в Санкт-Петербурге [53] и в 1998 году в Москве [46], на III Краковской международной конференции по теории графов в 1997 году [52], на Пятом чехо-словацком симпозиуме по комбинаторике, теории графов, алгоритмам и приложениям в 1998 году [47], на конференции "Случайные структуры и алгоритмы" в Познани в 1999 году, на международной конференции памяти П. Эрдеша в Будапеште в 1999 году [48], на семинаре кафедры высшей алгебры Московского государственного университета, на семинаре "Экстремальные задачи теории графов" в Институте математики СО РАН, на семинаре отдела алгебры и топологии Института математики и механики УрО РАН, на городском алгебраическом семинаре в Уральском государственном университете.
Основные результаты диссертации опубликованы в работах [41]-[57]. Работы [51]-[57] написаны в нераздельном соавторстве с А.А. Махневым. Из работы [41] в диссертации использованы только результаты, принадлежащие автору.
В заключение хочу выразить свою глубокую благодарность научному консультанту доктору физ.-мат. наук, профессору А.А. Махневу.
АВТОРЕФЕРАТ
Теорема 1
Теорема 2
Теорема 3
Теорема 4
Теорема 5
Теорема 6
Теорема 7
Теорема 8
Теорема 9
Теорема 10