Up: НЕКОТОРЫЕ КОНЕЧНО-АДДИТИВНЫЕ ВЕРСИИ РАВНОМЕРНОГО Previous: 4 Некоторые свойства
Следует отметить, что аналогичные конструкции можно построить на
семействе
![]() N всех подмножеств натурального ряда
N всех подмножеств натурального ряда ![]() . Именно,
рассмотрим полуалгебру
. Именно,
рассмотрим полуалгебру ![]() подмножеств
подмножеств ![]() , состоящую из
конечных и бесконечных промежутков
, состоящую из
конечных и бесконечных промежутков ![]() . Тогда функцию
. Тогда функцию
![]() , значения которой равны 0 на конечных и 1
на бесконечных промежутках, можно, в некотором "аппроксимативном
смысле", трактовать как "равномерное" распределение на
, значения которой равны 0 на конечных и 1
на бесконечных промежутках, можно, в некотором "аппроксимативном
смысле", трактовать как "равномерное" распределение на ![]() .
Функция
.
Функция
![]() является чисто к.-а. мерой на
является чисто к.-а. мерой на ![]() и,
аналогично случаю отрезка
и,
аналогично случаю отрезка ![]() , можно указать чисто к.-а. меру
определенную на
, можно указать чисто к.-а. меру
определенную на
![]() N и являющуюся продолжением
N и являющуюся продолжением
![]() .
При этом
.
При этом
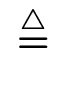 {
{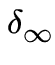 } =
} =
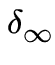 } =
} =
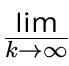 f (k)
f (k)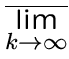 f (k)}
f (k)}
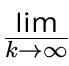 f (k)
f (k)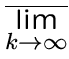 f (k)}.
f (k)}.