Статья из журнала МИФ.

Результат работы конвертора TTH.

File translated from TE X by TT H, version 2.01.

Глава 1
Областная олимпиада по физике З.И. Урицкий

  Итоги олимпиады

Областная олимпиада по физике, проводимая Департаментом образования Свердловской области и Уральским государственным университетом, состоит из нескольких этапов. Осенью проводятся районные, городские и заочная олимпиады. Победители приглашаются на областную олимпиаду, состоящую из двух туров - теоретического и практического.

В этом году для участия в областном туре олимпиады было приглашено 127 школьников. Из них учащихся 9 классов 37 (11, здесь и далее в скобках указано число участников из Екатеринбурга), учащихся 10 классов 37 (16), учащихся 11 классов 50 (16).

Победителями олимпиады стали:

9 класс.

1 место - Панченко Андрей (N18, Н-Тагил),

2 место - Барыкин Никита (N9, Екатеринбург),

3 место - Домуховский Николай (N94, Екатеринбург) и Матвеев Егор (N82, Н-Тагил).

10 класс. 1 место - Боярченков Алексей (СУНЦ, Екатеринбург),

2 место - Кокшаров Дмитрий (N9, Екатеринбург) и Седельников Вадим (СУНЦ, Екатеринбург),

3 место - Спесивцев Леонид (N9, Екатеринбург).

11 класс.

1 место - Патраков Александр (СУНЦ, Екатеринбург),

2 место - Исаев Виктор (N9, Екатеринбург),

3 место - Хафизулин Руслан (N82, Н-Тагил), Шахмаев Андрей и Черных Александр (СУНЦ, Екатеринбург)

Победители и лауреаты были награждены ценными призами, дипломами, приглашены на летнюю школу СУНЦ. Выпускники школ, победители олимпиады, получили право быть зачисленными на физический факультет УрГУ. В этом году Оргкомитет Олимпиады решил не ограничиваться словами поздравления в адрес учителей, чьи воспитанники показали хорошие результаты. На закрытии дипломами Оргкомитета были награждены преподаватели физики СУНЦ УрГУ, школы - гимназии N9, политехнической гимназии, и др.

Задачи.

  9 класс
  Решения задач

  9 класс

1. Определить, в какую сторону от вертикали и на сколько отклонится в высшей точке полета снаряд, запущенный на экваторе Земли в вертикальном направлении. Начальная скорость снаряда 800 м/с. Сопротивлением воздуха пренебречь. Решение

2. В цилиндрическом сосуде с водой плавает дощечка, на которой находится железный куб. На сколько изменится уровень воды в сосуде, когда куб, упав с дощечки, будет находится на дне сосуда? Площадь дна сосуда, длина ребра куба, плотность воды, плотность железа соответственно равны S, a, r0, rж. Решение

3. Определить с каким ускорением будет двигаться система грузов при произвольных значениях m1, m2 (массы грузов) и m (коэффициент трения груза m1 с наклонной плоскостью).


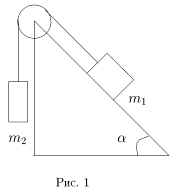
Picture 1

Каково при этом должно быть соотношение между массами грузов? В начальный момент грузы неподвижны, угол a задан. Считать, что нить и блок невесомы, нить нерастяжима, трением в блоке можно пренебречь. Дать качественное описание изменения силы трения при изменении масс грузов. Решение

4. В лифте находится ведро с водой, в которой плавает мяч. Как изменится глубина погружения мяча, если лифт будет двигаться с ускорением a, направленным вверх? направленным вниз?

  Решения задач


1. Простейшая оценка определяется тем, что линейная скорость на поверхности Земли отличается от скорости на высоте H

V1 = wR = 2pR
T
 ,    V2 = 2p(R + H )
T
 ,
где
H = V02
2g
максимальная высота подъема снаряда.

Время подъема найдем по формуле

t = V0
g
 .

Таким образом, снаряд "отстанет" от точки на продолжении радиуса R на расстояние

l = ( V2 - V1 ) t = 2p
T
 H Vo
g
 ,
где T - период обращения Земли.


2. Уровень воды изменится, так как объем, вытесненный кубом воды, отличается на

DV = V0 rж
r0
 - V0 = V0( rж
r0
 - 1).

В первом случае объем воды определяется тем, что вес вытесненной жидкости равен весу куба, а во втором  - объем вытесненной воды равен объему куба.

Dh = DV
S
 , V0 = a3.


3. Рассмотрим две различных ситуации.

1. Тела двигаются так, что тело массой m1 движется вверх по наклонной плоскости:

m2g-m1gsina-mm1gcosa = (m1+m2)a1 Ё 0,
m2/m1 Ё sina+mcosa.     (1)
2. Тела двигаются так, что тело массой m1 движется вниз по наклонной плоскости:
m1gsina-mm1gcosa-m2g = (m1+m2)a2 Ё 0,
m2/m1 ё sina-mcosa.     (2)
В первом случае сила трения покоя направлена вниз, во втором случае она направлена вверх ( вдоль наклонной плоскости ) и меняется от mm1gcosa до нуля, когда m2 = m1sina.

Неравенства (1) и (2) легко позволяют записать условия, при которых тела будут двигаться с постоянной скоростью или покоиться.


4. Не изменится, пока a ╧ g, так как изменяется и вес m(g╠a) и выталкивающая сила rV( g ╠a ). При g = a (свободное падение) и вес, и выталкивающая сила равны нулю.

Задачи

  10 класс
  Решения задач

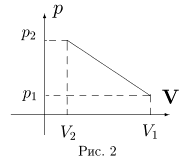
  10 класс

1. Найти максимальную температуру в процессе, изображенном на рисунке. Количество газа - 1 моль.


Picture 1

Решение

2. В металлическом шаре массой M и радиусом R, на расстоянии от центра 3R/4, сделана сферическая полость радиуса R/4. Определить силу притяжения между этим шаром и маленьким шариком массы m, находящимся на расстоянии r по прямой, проходящей по диаметру полости. Решение

3. Две бусинки с массами m1 и m2 нанизаны на горизонтальный стержень так, что могут перемещаться по нему без трения, и соединены нерастяжимой длинной нитью l. Стержень равномерно вращают вокруг вертикальной оси, расположенной между бусинками. Бусинка m1 соединена с осью невесомой пружиной жесткости k и длиной s (в недеформированном состоянии). При каком положении бусинок относительно оси вращения не будет происходить перемещение бусинок по стержню. При какой угловой скорости это положение будет устойчивым? Решение

4. Пуля летит с постоянной скоростью и гонит перед собой воздушный слой некоторой толщины со скоростью V.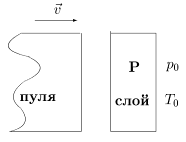


Picture 2

Давление внутри слоя P. На сколько изменяется температура на границе фронта при заданных температуре T0 и давлении P0 окружающего воздуха? Взаимодействие и теплообмен слоя перед пулей с окружающим воздухом не учитывать. Пулю рассматривать в виде цилиндра. Решение

  Решения задач


1. Чтобы найти температуру, нужно найти точки пересечения наклонной на графике и гиперболы PV = R T, причем две точки пересечения должны сливаться в одну.

Решаем систему уравнений

PV = R T,
P = P1- P2-P1
V2-V1
 (V-V1).
Получим, исключая P, квадратное уравнение
( P2 - P1 )V2 -( V1P2 - P1V2)V+ RT(V1-V2) = 0.
Два корня совпадают, если
(V1P2-P1V2)2-4RT(P2-P1)(V1-V2) = 0.
Отсюда
T = (V1P2-V2P1)2
4R(P2-P1)(V1-V2)
 .


2. Будем рассматривать силу притяжения как разность силы притяжения к сплошному шару радиуса R и силы притяжения к шару радиуса R/4, который соответствует полости. Масса большого шара М1, малого М2.

M1
M2
 = ж
з
и 		R
R/4
 ц
ч
ш 		3 = 64.
Так как M1-M2 = M, то
M1 = M
63
 ,     M2 = M
63
 .
Для силы (по модулю) получим
F = GmM1
r2
 - GmM2
(r-3R/4)2
 = GmM
63r2
 й
к
л 		1- 1
(1-3R/4r)2
 щ
ъ
ы 		.


3. Стационарное вращение бусинок определяется уравнениями Ньютона

m1w2r1 = T+k(r1-S),
m2w2r2 = T,
где r1 и r2 - расстояние бусинок от оси, T - натяжение нити, r1+r2 = l - расстояние между бусинками.

Подставляя r2 и T в первое уравнение, получим

r1 = m2w2l-kS
(m1+m2)w2-k
 ,   r2 = m1w2l-k(l-S)
(m1+m2)w2-k
и T = m2w2r2.

Так как r1 и r2 положительны, числитель и знаменатель должны быть либо положительны, либо отрицательны. В первом случае пружина растянута, во втором - сжата. При устойчивом равновесии смещение бусинок должно привести к появлению силы, направленной против смещения, т.е.

(m1+m2)w2Dr - kDr > 0 или w2 > k
m1+m2
 .


4. Пуля при движении совершает работу, сжимая слой воздуха до давления P за счет силы F = SDP, где S - площадь сечения пули.

Эта сила изменяет плотность и импульс воздушной подушки

FDt = SDPDt = mV-m0V = SVDtDrV,
где SVDt - объем сжимаемого слоя. Отсюда находим
Dr = DP
V2
 = m
u
 - m
u0
 = m
R
 ( P
T
 - P0
T0
 ),
u и u0 - объем воздуха, сжимаемого пулей от u0 до u, тогда
DT = T0( mV2-RT0
mV2P0T0RtDP
 ).

Задачи

  11 класс
 Решения

  11 класс

1. На систему, состоящую из двух соединенных пружиной шариков массы m, покоящуюся на гладкой горизонтальной поверхности, налетает слева шарик массы M.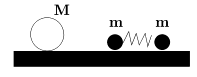


Picture 1

Происходит лобовой абсолютно упругий удар. Найти отношение масс g = m/M, при котором удар произойдет еще раз.

Решение

2. Цилиндрическая камера (рис. 0.1) длиной 2l с поршнем сечением S (общая масса M) может двигаться по горизонтальной плоскости с коэффициентом трения m. Слева от поршня, расположенного в центре камеры, находится газ при температуре T0 и давлении P0. Между неподвижной стенкой и поршнем помещена пружина жесткости k. Во сколько раз нужно увеличить температуру газа слева от поршня, чтобы его объем удвоился, если между камерой и поршнем трения нет? Наружное давление равно P0. Решение

3. Электроны ускоряются в электронной пушке электрическим полем, проходя отрезок пути, напряжение на концах которого U = 103B. Вылетев из пушки в точке A, электроны движутся затем по прямой AN (рис. 0.1). В точке M на расстоянии d = 5 см от точки A находится мишень, причем прямая AM образует угол a = 600 с прямой AN. Какой должна быть индукция в случае а) однородного магнитного поля В, перпендикулярного плоскости рисунка, или в случае б) однородного магнитного поля B1, параллельного прямой AM, для того, чтобы электроны попадали в мишень и в том, и в другом случае? Считать, что модули векторов индукции В и B1 не превышают 0,03 Тл. Решение


Picture 2

4. Переменный конденсатор с начальной емкостью C0, заряженный до напряжения U, замыкают на резистор с сопротивлением R (рис. 0.1). Как нужно изменять со временем емкость конденсатора, чтобы в цепи шел постоянный ток? Какую мощность развивают внешние силы, благодаря которым изменяется емкость конденсатора? Решение

  Решения


1. Очевидно, что второй удар произойдет, если скорость шарика М после удара направлена в сторону движения шариков m

MV = MV╒+mV1.
Рассматриваем удар с одним шариком, так как время удара мало по сравнению с временем, за которое сжимающаяся пружина начнет передавать импульсы второму шарику. Записав закон сохранения энергии
MV2
2
 = MV╒2
2
 + mV12
2
 ,
Найдем
V╒ = M-m
M+m
 V,     V1 = 2M
M+m
 V.
Ясно, что
V╒ > 0 если M > m.
Центр масс системы двух шариков будет перемещаться со скоростью
V2 = 1
2
 V1 = M
M+m
 V.
Второе столкновение произойдет, если через 3/4 периода колебаний, когда расстояние между шариками будет максимальным, шар М догонит шарик m.

Период колебаний определится как период колебаний одного из шариков относительно центра масс и равен

(Формула ниже -- gif-образ:)


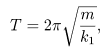
Picture 3

где k1 - жесткость половины пружины, k1 = 2k, k - жесткость пружины длины l0.

За это время шар M пройдет расстояние

(Формула ниже -- gif-образ:)


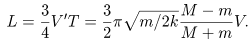
Picture 4

Шарик m пройдeт расстояние

l = 3
4
 V2T-x0,
где x0 - амплитуда колебаний шариков, определяемая из закона сохранения энергии:
mV12
2
 = k(2x0)2
2
 + 2mV22
2
 ,

(Формула ниже -- gif-образ:)


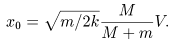
Picture 5

Второй удар произойдeт, если L Ё l

(Формула ниже -- gif-образ:)


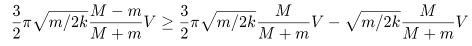
Picture 6

или     m
M
 < 2
3p
 .
Более точное решение можно получить, рассматривая равенство
V╒t = V2t-x0sin(wt),
т.е. решая традиционное уравнение.


2. Следует рассмoтреть два случая:

1. Камера покоится (mmg Ё kl)

(P-P0)S = kl , P 2Sl
T
 = P0 Sl
T0
 .
Отсюда
T
T0
 = 2 ж
з
и 		1+ kl
PS
 ц
ч
ш 		.

2. Камера покоится до момента достижения максимального значения силы трения покоя. Найдем соответствующую этому моменту температуру T╒. Деформация пружины

x = mmg
k
 ,
кроме того
P-P0 = mmg
S
 , PS(l+x)
T╒
 = P0Sl
T0
 ,
T╒
T
 = ж
з
и 		1+ mmg
P0S
 ц
ч
ш 		ж
з
и 		1+ mmg
kl
 ц
ч
ш 		.
После возникновения проскальзывания камеры процесс увеличения объема идет при постоянном давлении:
T
T╒
 = V
V0
 = 2lS
(l+x)S
 = 2
1+mmg/kl
 .
Подставляя в это выражение Т╒, получаем
T
T0
 = 2 ж
з
и 		1+ mmg
P0S
 ц
ч
ш 		.


3. а) Электроны попадут в мишень, если AM будет другой окружности, которая является траекторией электронов в магнитном поле В. Скорость электронов определяется из условия

(Формула ниже -- gif-образ:)


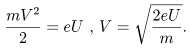
Picture 7

Сила Лоренца определится соотношением

eVB = mV2
R
 .

Радиус R найдeм из условия, что AM отсекает сектор с углом a

R = d
2sina
 .
Используя это равенство, получаем

(Формула ниже -- gif-образ:)


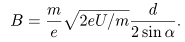
Picture 8

б) В этом случае электрон летит по винтовой линии

V╒╒ = Vcosa и V╒ = Vsina,
где V╒╒ - проекция скорости электрона на направление AM, V╒ - на перпендикулярное AM направление.

Расстояние d электрон пролетит за время

t = d
Vcosa
 .
За это время он должен сделать в магнитном поле В целое число оборотов t = nT, где T - период обращения электрона в магнитном поле
B = mVsina
eR
 ,
T = 2pR
Vsina
 = 2pmVsina
VsinaeB
 = 2pm
eB
 .
Таким образом,
d
Vcosa
 = 2pm
eB
 n , B = 2pmn
ed
 Vcosa,
где n = 1,2,...


4. Ток в цепи

I = Dq
Dt
 = D(CU)
Dt
 = const , U = IR = const , отсюда DC
Dt
 ,
т.е. емкость должна меняться линейно со временем: C = C0+at.