ТРУДЫ ИНСТИТУТА МАТЕМАТИКИ И МЕХАНИКИ УрО
РАН
Contents
Том 6 N1 2000
УДК 517.9
НEКОТОРЫЕ ОЦЕНКИ МНОЖЕСТВА ДОСТИЖИМОСТИ ДЛЯ УПРАВЛЯЕМОГО УРАВНЕНИЯ ВАН ДЕР ПОЛЯ1
М. С. Никольский, Мусса Абубакар
Рассматривается известное уравнение Ван дер Поля при наличии управляющих
воздействий. Получены оценки множеств достижимости этого управляемого
объекта в фазовом пространстве сверху и снизу (т.е. извне и изнутри). При
этом использован аппарат функций Ляпунова и одна теорема о накрытии
нелинейным отображением.
В теории колебаний весьма большое
значение придается изучению
свойств решений широко известного уравнения
Ван дер Поля (см., например, [1]-[3]).
Мы рассмотрим это уравнение при наличии воздействий
(которые мы интерпретируем как управления) в следующем виде:
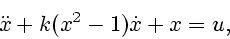 |
(1) |
где константа 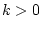 , а скалярное управление
, а скалярное управление 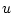 удовлетворяет
ограничению
удовлетворяет
ограничению 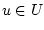 ,
, ![$U = [p,q]$](img5.gif) , причем
, причем 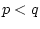 и
и ![$ 0 \in [p, q]$](img7.gif) .
.
Будем считать, что начальные условия для уравнения (1) имеют
простейший вид
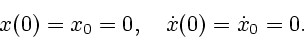 |
(2) |
Управления 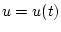 ,
, ![$t \in [0,T]$](img10.gif) ,
, 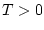 , будем рассматривать в классе
измеримых по Лебегу функций, как это обычно делается в математической
теории управления (см., например, [4], [5]). Полагая
, будем рассматривать в классе
измеримых по Лебегу функций, как это обычно делается в математической
теории управления (см., например, [4], [5]). Полагая 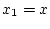 ,
, 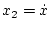 , перепишем уравнение (1) в виде системы
уравнений
, перепишем уравнение (1) в виде системы
уравнений
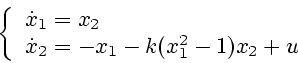 |
(3) |
с начальными условиями
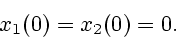 |
(4) |
Решения
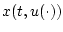 системы (3), (4) рассматриваются в классе
абсолютно непрерывных функций (см. [4], [5]). Нас будет
интересовать множество достижимости
системы (3), (4) рассматриваются в классе
абсолютно непрерывных функций (см. [4], [5]). Нас будет
интересовать множество достижимости 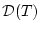 (см. [5]) системы
(3), (4). Напомним, что
(см. [5]) системы
(3), (4). Напомним, что
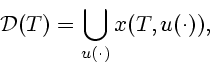 |
(5) |
где объединение берется по всевозможным измеримым управлениям 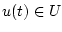 ,
, ![$t \in [0,T]$](img10.gif) . Так как
. Так как 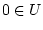 , то
, то
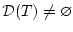 и
и
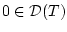 .
.
Перейдем к оценке сверху множества 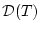 . Для этого удобно рассмотреть
новую управляемую систему (сравните с (3), (4))
. Для этого удобно рассмотреть
новую управляемую систему (сравните с (3), (4))
![\begin{displaymath}
\left\{
\begin{array}{l}
\displaystyle
\dot{y}_1 = y_2 - k\l...
..., \\ [2ex]
\displaystyle
\dot{y}_2 = - y_1,
\end{array}\right.
\end{displaymath}](img23.gif) |
(6) |
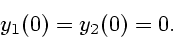 |
(7) |
Подобный переход в связи с задачами устойчивости делался, например, в
[3].
Отметим, что компонента
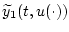 решения задачи Коши (6),
(7), отвечающая произвольному измеримому управлению
решения задачи Коши (6),
(7), отвечающая произвольному измеримому управлению 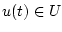 ,
,
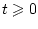 , удовлетворяет уравнению (1), а векторная функция
, удовлетворяет уравнению (1), а векторная функция
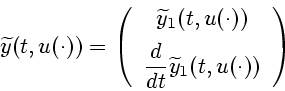 |
(8) |
является решением задачи Коши вида (3), (4).
В силу этого полезно получить оценки функций
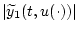 ,
,
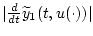 при
при ![$t \in [0,T]$](img10.gif) . Для получения
оценки функции
. Для получения
оценки функции
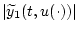 воспользуемся простейшей функцией
Ляпунова
воспользуемся простейшей функцией
Ляпунова
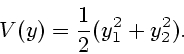 |
(9) |
Для производной функции 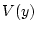 вдоль траекторий системы (6) при данном
измеримом управлении
вдоль траекторий системы (6) при данном
измеримом управлении  ,
,  получаем из элементарных
соображений априорные неравенства
получаем из элементарных
соображений априорные неравенства
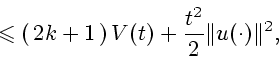 |
(10) |
где
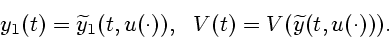 |
(11) |
При выводе неравенства (10) мы использовали следующие неравенства:
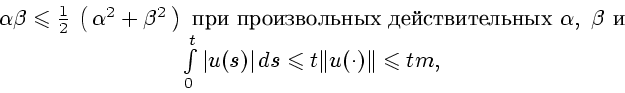 |
(12) |
где 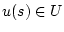 - произвольная измеримая функция на
- произвольная измеримая функция на ![$[0,T]$](img37.gif) ,
, ![$t \in [0,T]$](img10.gif) ,
,
![\begin{displaymath}
\Vert{u(\cdot)}\Vert = \mathop{\rm Vrai\,sup}\limits_{t \in [0,T]} \vert u(t)\vert,
\end{displaymath}](img38.gif) |
(13) |
т.е. мы используем норму пространства
![$L_{\infty}[0,T]$](img39.gif) (см. [6]),
(см. [6]),
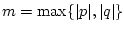 . Отметим, что из ограниченности
измеримой функции
. Отметим, что из ограниченности
измеримой функции 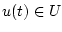 ,
, 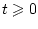 ,
априорных неравенств (10) и формулы
(9) вытекает (см., например, [3]), что решение
,
априорных неравенств (10) и формулы
(9) вытекает (см., например, [3]), что решение
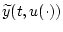 задачи (6), (7) продолжимо на всю полуось
задачи (6), (7) продолжимо на всю полуось 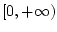 для каждого измеримого управления
для каждого измеримого управления 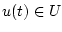 ,
, 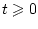 . Имеет
место также единственность решения
. Имеет
место также единственность решения
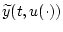 при
при 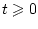 .
.
Из соотношений (9)-(13) с помощью аппарата дифференциальных
неравенств (см., например, [7]) получаем следующие неравенства при
![$t \in [0,T]$](img10.gif) для произвольной измеримой функции
для произвольной измеримой функции 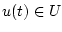 :
:
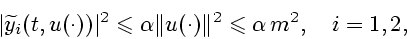 |
(14) |
где
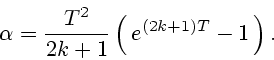 |
(15) |
Теперь займемся оценкой функции
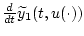 при
произвольной измеримой функции
при
произвольной измеримой функции 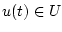 ,
, ![$t \in [0,T]$](img10.gif) . Обозначим
. Обозначим

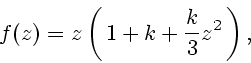 |
(16) |
где 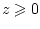 . Из (6), (14), (16) при
. Из (6), (14), (16) при ![$t \in [0,T]$](img10.gif) получаем неравенства
получаем неравенства
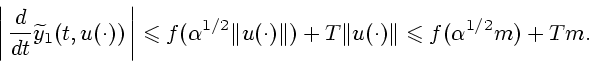 |
(17) |
Так как функция (8) является решением задачи Коши (3),
(4), то из сказанного при ![$t \in [0,T]$](img10.gif) и произвольной измеримой
функции
и произвольной измеримой
функции 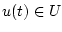 , получаем следующие неравенства (см.
(14)-(17)):
, получаем следующие неравенства (см.
(14)-(17)):
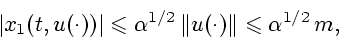 |
(18) |
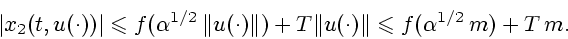 |
(19) |
Отметим, что из (16), (19) вытекает следующее
неравенство при ![$t \in [0,T]$](img10.gif) :
:
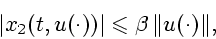 |
(20) |
где
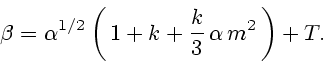 |
(21) |
Далее переходим к оценке множества достижимости  изнутри.
Условимся через
изнутри.
Условимся через
 обозначать внутренность множества
обозначать внутренность множества
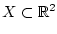 . Мы будем искать
некоторый эффективно вычислимый выпуклый
компакт
. Мы будем искать
некоторый эффективно вычислимый выпуклый
компакт 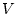 , для которого выполняется включение
, для которого выполняется включение
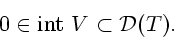 |
(22) |
Для получения таких оценок можно применить следующую теорему о
накрытии (см. [8]).
Пусть нелинейное непрерывное отображение 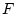 отображает ограниченное
выпуклое множество
отображает ограниченное
выпуклое множество 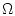 из действительного банахова пространства
из действительного банахова пространства 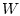 в
в 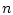 -мерное евклидово пространство
-мерное евклидово пространство 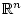 . Пусть далее
. Пусть далее 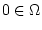 ,
,
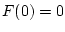 и при
и при
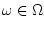
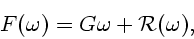 |
(23) |
где 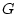 - линейный ограниченный оператор, действующий из
- линейный ограниченный оператор, действующий из 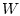 в
в 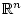 ,
,
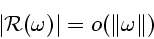 |
(24) |
при 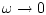 ,
,
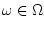 (
(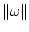 означает длину
вектора
означает длину
вектора 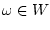 ,
,
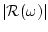 - длину вектора
- длину вектора
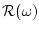 из
из 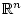 ).
).
З а м е ч а н и е. Отметим, что в условиях теоремы не обязательно
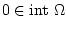 . По
поводу других теорем о накрытии смотрите например,
. По
поводу других теорем о накрытии смотрите например,
[8] и [9].
Возьмем
![$W = L_{\infty}([0, T])$](img86.gif) (см. теорему). Пусть
(см. теорему). Пусть 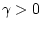 столь велико, что
столь велико, что
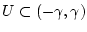 . Аналогично
вышесказанному можно показать, что на открытом шаре
. Аналогично
вышесказанному можно показать, что на открытом шаре
![$\Lambda \subset
L_{\infty}([0, \infty])$](img89.gif) с центром в
с центром в 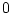 и радиуса
и радиуса 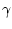 определен
нелинейный оператор
определен
нелинейный оператор
Используя гладкость правой части системы (3), можно обосновать
непрерывность и дифференцируемость по Фреше (см. [6]) оператора
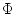 на
на 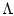 . В частности, оператор
. В частности, оператор 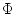 дифференцируем по Фреше
при
дифференцируем по Фреше
при 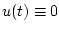 ,
, ![$t \in [0,T]$](img10.gif) и, как можно показать, при
и, как можно показать, при
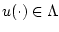 справедливо разложение
справедливо разложение
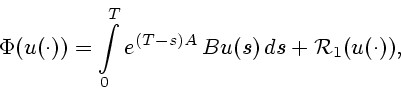 |
(25) |
где
![\begin{displaymath}
A = \left(\begin{array}{cc} {0}, & {1} \\ [2ex] {-1}, & {k}
...
...= \left(\begin{array}{c} {0} \\ [1ex] {1}
\end{array}\right),
\end{displaymath}](img97.gif) |
(26) |
В качестве выпуклого множества  (см. теорему) мы возьмем множество
функций
(см. теорему) мы возьмем множество
функций
![${u(\cdot)}\in L_{\infty}([0, \infty])$](img99.gif) таких, что почти всюду на
таких, что почти всюду на ![$[0,T]$](img37.gif)
 . Отметим, что
. Отметим, что 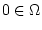 ,
,
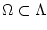 .
.
Рассмотрим теперь линейный ограниченный оператор 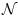 , действующий из
, действующий из
![$L_{\infty}([0, \infty])$](img102.gif) в
в 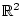 по формуле (см. (25), (26))
по формуле (см. (25), (26))
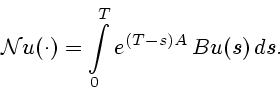 |
(27) |
Для изучения множества
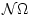 полезно ввести многозначное
отображение
полезно ввести многозначное
отображение
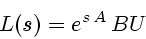 |
(28) |
при ![$s \in [0,T]$](img107.gif) и рассмотреть от него интеграл (см. [6],
[10])
и рассмотреть от него интеграл (см. [6],
[10])
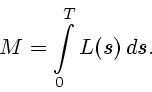 |
(29) |
С помощью [6], [10] можно обосновать, что 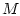 - выпуклый
компакт и что
- выпуклый
компакт и что
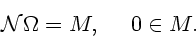 |
(30) |
Множество 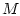 (см. (29)) является множеством достижимости
(см. (29)) является множеством достижимости 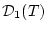 в момент
в момент 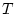 (см. [5]) линеаризованного объекта (1):
(см. [5]) линеаризованного объекта (1):
![\begin{displaymath}
\left\{
\begin{array}{l}
\dot{x}_1 = x_2 \\ [2ex]
\dot{x}_2 = k x_2 - x_{1} + u
\end{array}\right.
\end{displaymath}](img113.gif) |
(31) |
Теперь оценим член
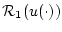 в формуле (25). С помощью формулы
Коши можно записать (см. (3), (7))
в формуле (25). С помощью формулы
Коши можно записать (см. (3), (7))
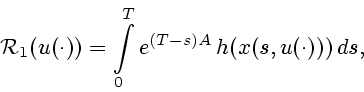 |
(32) |
где
![\begin{displaymath}
h(x) = \left(\begin{array}{c} {0} \\ [1ex] {-kx_{1}^{2}x_2}
\end{array}\right),
\end{displaymath}](img117.gif) |
(33) |
причем
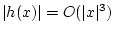 при
при 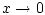 . Итак,
. Итак,
![\begin{displaymath}
{\cal R}_1({u(\cdot)}) = \int\limits^{T}_{0} e^{(T-s)A}
\lef...
... {0} \\ [1ex] {-kx_{1}^{2}(s)x_2(s)}
\end{array}\right)\, ds.
\end{displaymath}](img120.gif) |
(34) |
Из соотношений (18), (19), (33) вытекает, что
![\begin{displaymath}
\mathop{\rm Vrai\,sup}\limits_{s \in [0,T]} \vert h(x(s, u(s)))\vert = o (\Vert{u(\cdot)}\Vert),
\end{displaymath}](img121.gif) |
(35) |
при
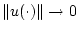 . Полагая
. Полагая
![$W = L_{\infty}([0, T])$](img86.gif) ,
,
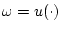 ,
, 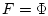 (см. (25)),
(см. (25)), 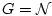 (см. (27)),
(см. (27)), 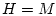 ,
,
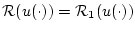 (см. (25), (34)), мы приходим в силу (35)
к соотношениям (23) и (24).
(см. (25), (34)), мы приходим в силу (35)
к соотношениям (23) и (24).
Для получения оценки
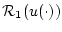 нам понадобится еще выражение для
нам понадобится еще выражение для
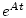 в явном виде. Рассмотрим сначала случай, когда
в явном виде. Рассмотрим сначала случай, когда 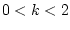 . Тогда
. Тогда
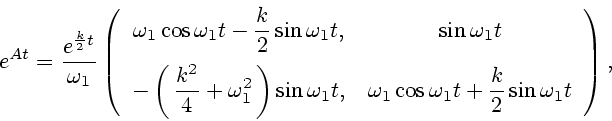 |
(36) |
где
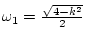 . Подставляя (36) в
(34), получаем
. Подставляя (36) в
(34), получаем
Используя (18) и (20), отсюда получаем
т.е.
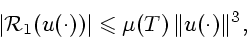 |
(37) |
где
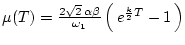 .
.
Далее, при
 (см. (28))
(см. (28))
![\begin{displaymath}
L(r) = \frac{e^{\frac{k}{2}r}}{\omega_1} \bigcup\limits_{u \...
...+ \frac{k}{2}\sin \omega_1
r}
\end{array}\right) u \,\right].
\end{displaymath}](img137.gif) |
(38) |
Рассмотрим опорную функцию 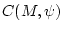 (см. [10]) для выпуклого
компакта
(см. [10]) для выпуклого
компакта 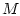 (см. (29)):
(см. (29)):
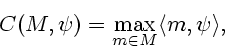 |
(39) |
где
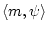 означает скалярное произведение векторов
означает скалярное произведение векторов
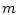 и
и 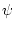 из
из 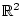 . Остановимся на случае, когда
. Остановимся на случае, когда ![$U = [0, q]$](img143.gif) , где
, где
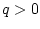 . Такой случай представляет интерес для экономических приложений
(см. [12], [13]). Используя свойства интеграла от
многозначного отображения (см. [10]), а также формулы (28),
(38), (39), можно показать, что
. Такой случай представляет интерес для экономических приложений
(см. [12], [13]). Используя свойства интеграла от
многозначного отображения (см. [10]), а также формулы (28),
(38), (39), можно показать, что
![\begin{displaymath}
C(M, \psi) = q \int\limits^{T}_{0}
\frac{e^{\frac{k}{2}r}}{\...
...omega_1 r
+ \psi_2 \omega_1 \cos \omega_1 r\,\right]^{+}\, dr,
\end{displaymath}](img145.gif) |
(40) |
где 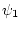 ,
, 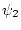 - компоненты вектора
- компоненты вектора
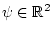 и
и
При условии 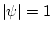 величины
величины
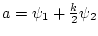 ,
,
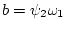 удовлетворяют неравенству
удовлетворяют неравенству 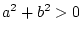 . Формулу (40)
можно переписать в виде
. Формулу (40)
можно переписать в виде
Очевидно, что существует такой угол
![$\varphi (\psi) \in [0, 2\, \pi]$](img155.gif) , что
, что
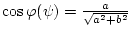 ,
,
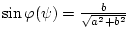 .
Следовательно,
.
Следовательно,
![\begin{displaymath}
C(M, \psi) = \sqrt{a^2 + b^2}\, q
\int\limits^{T}_{0} \frac{...
...bigl[\, \sin ( \omega_1 r + \varphi (\psi))\,\bigr]^{+} \, dr.
\end{displaymath}](img158.gif) |
(41) |
Из (41) следует, что при
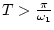 и
и ![$U = [0, q]$](img143.gif) ,
где
,
где 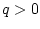 , для произвольного
, для произвольного 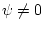
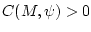 . С помощью
выпуклого анализа (см., например, [10]) отсюда получаем, что при
. С помощью
выпуклого анализа (см., например, [10]) отсюда получаем, что при
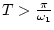
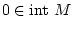 и что радиус
и что радиус 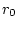 максимального
шара с центром в
максимального
шара с центром в 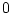 , содержащегося в
, содержащегося в 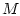 , определяется формулой
, определяется формулой
![\begin{displaymath}
r_0 = q \min\limits_{\varphi \in [0, 2\, \pi]}\,
\biggl\{\sq...
... \bigl[ \sin ( \omega_1 r +
\varphi )\bigr]^{+} \, dr\biggr\}.
\end{displaymath}](img164.gif) |
(42) |
Применяя теорему о накрытии (см. выше), можно заключить, что при
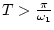
где величина
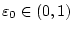 находится из неравенства (см. (37))
находится из неравенства (см. (37))
опорная функция выпуклого компакта 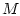 определяется формулой (41),
а величина
определяется формулой (41),
а величина 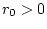 дается формулой (42). Случай
дается формулой (42). Случай ![$U = [-q, q]$](img168.gif) , где
, где
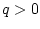 , рассматривается с очевидными изменениями. Причем
, рассматривается с очевидными изменениями. Причем
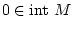 при
любом
при
любом 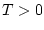 .
.
Пусть 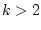 и
и ![$u \in [-1,1]$](img170.gif) . В этом случае
. В этом случае
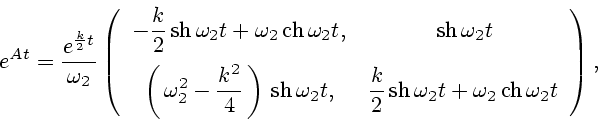 |
(43) |
где
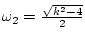 ,
,
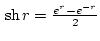 ,
,
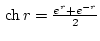 ,
,
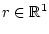 .
Подставляя (43) в (34), получим
.
Подставляя (43) в (34), получим
Отсюда получаем, с помощью элементарных вычислений, что
Используя (18) и (20), далее получаем:
Таким образом,
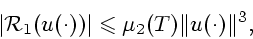 |
(44) |
где
Далее, при
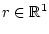 рассмотрим многозначное отображение
рассмотрим многозначное отображение
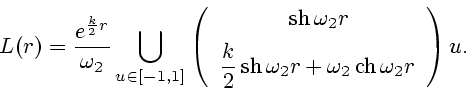 |
(45) |
Как и в предыдущем случае, рассмотрим опорную функцию 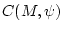 для
выпуклого компакта
для
выпуклого компакта 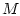 (см. (29), (39)). Используя свойства
интеграла от многозначного отображения (см. [10]), в также формулы
(28), (39), (45), можно показать, что
(см. (29), (39)). Используя свойства
интеграла от многозначного отображения (см. [10]), в также формулы
(28), (39), (45), можно показать, что
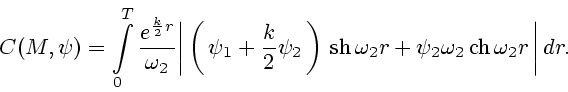 |
(46) |
Перепишем (46) в виде
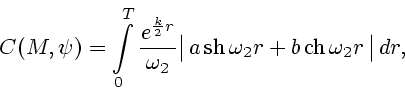 |
(47) |
где
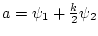 ,
,
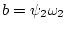 . Нетрудно
доказать, что функции
. Нетрудно
доказать, что функции
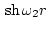 и
и
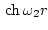 являются линейно независимыми на любом ненулевом отрезке, поэтому
являются линейно независимыми на любом ненулевом отрезке, поэтому
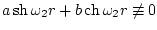 при
при 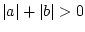 на любом ненулевом отрезке. Следовательно,
на любом ненулевом отрезке. Следовательно, 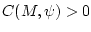 для
любого
для
любого 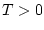 и для любого
и для любого 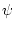 из единичной окружности. С помощью
выпуклого анализа (см. [10]) отсюда получаем,
что
из единичной окружности. С помощью
выпуклого анализа (см. [10]) отсюда получаем,
что
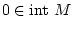 для любого
для любого 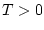 и что радиус
и что радиус 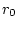 максимального шара с центром в
максимального шара с центром в 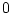 ,
содержащегося в
,
содержащегося в 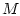 , определяется формулой
, определяется формулой
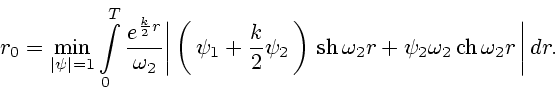 |
(48) |
Применяя теорему о накрытии и неравенство (44), можно утверждать,
что для любого 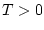
где величина
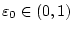 находится из неравенства
находится из неравенства
Опорная функция выпуклого компакта 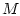 определяется формулой (47).
определяется формулой (47).
Случай, когда ![$U = [-q, q]$](img168.gif) , где
, где 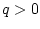 ,
анализируется с очевидными изменениями.
,
анализируется с очевидными изменениями.
При 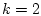 получаем
получаем
![\begin{displaymath}
e^{At} = e^{t} \left(\begin{array}{cc} {1-t}, & {t} \\ [2ex] {-t}, & {1+t}
\end{array}\right).
\end{displaymath}](img191.gif) |
(49) |
Аналогично предыдущим случаям, подставляя (49) в
(34), получаем
Отсюда получаем, что
Используя (18) и (20), теперь получаем
т.е.
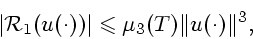 |
(50) |
где
Пусть ![$U = [-1,1]$](img197.gif) . Тогда при
. Тогда при
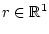 (см. (28))
(см. (28))
![\begin{displaymath}
L(r) = e^r \bigcup\limits_{u \in [-1,1]} \left(\begin{array}{c} {r} \\ [1ex] {1+r}
\end{array}\right) u.
\end{displaymath}](img198.gif) |
(51) |
Рассмотрим опорную функцию 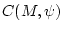 для
для 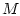 (см. (29)).
Используя свойства интеграла от многозначного отображения (см.
[10]), а также (29), (39), (51), можно показать,
что
(см. (29)).
Используя свойства интеграла от многозначного отображения (см.
[10]), а также (29), (39), (51), можно показать,
что
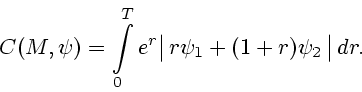 |
(52) |
Нетрудно далее показать, что для любого 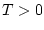 и для любого
и для любого 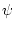 из
единичной окружности
из
единичной окружности 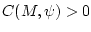 . С помощью выпуклого анализа (см.
[10]) получаем, что
. С помощью выпуклого анализа (см.
[10]) получаем, что
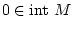 для любого
для любого 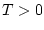 и радиус
и радиус 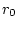 максимального шара с центром в
максимального шара с центром в 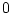 , содержащегося в
, содержащегося в 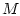 , определяется
формулой
, определяется
формулой
Применяя теорему о накрытии и неравенство (50), можно утверждать,
что для любого 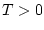
где величина
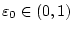 находится из неравенства
находится из неравенства
Случай ![$U = [-q, q]$](img168.gif) , где
, где 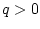 , можно рассмотреть аналогичным образом.
, можно рассмотреть аналогичным образом.
Можно было бы также во всех трех вариантах расположения числа 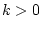 рассмотреть более общий случай:
рассмотреть более общий случай:
![$U = [-q_1, q_2]$](img202.gif) , где
, где 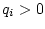 . Но
соответствующие формулы для нахождения величины
. Но
соответствующие формулы для нахождения величины
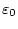 становятся
значительно сложнее по виду.
становятся
значительно сложнее по виду.
Поступила 1.10.1999


Next: Bibliography
u1904
2003-08-19
![]() системы (3), (4) рассматриваются в классе
абсолютно непрерывных функций (см. [4], [5]). Нас будет
интересовать множество достижимости
системы (3), (4) рассматриваются в классе
абсолютно непрерывных функций (см. [4], [5]). Нас будет
интересовать множество достижимости ![]() (см. [5]) системы
(3), (4). Напомним, что
(см. [5]) системы
(3), (4). Напомним, что
![]() . Для этого удобно рассмотреть
новую управляемую систему (сравните с (3), (4))
. Для этого удобно рассмотреть
новую управляемую систему (сравните с (3), (4))
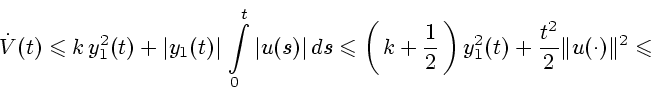
![]() для произвольной измеримой функции
для произвольной измеримой функции ![]() :
:
![]() при
произвольной измеримой функции
при
произвольной измеримой функции ![]() ,
, ![]() . Обозначим
. Обозначим
![]()
![]() изнутри.
Условимся через
изнутри.
Условимся через
![]() обозначать внутренность множества
обозначать внутренность множества
![]() . Мы будем искать
некоторый эффективно вычислимый выпуклый
компакт
. Мы будем искать
некоторый эффективно вычислимый выпуклый
компакт ![]() , для которого выполняется включение
, для которого выполняется включение
![]() отображает ограниченное
выпуклое множество
отображает ограниченное
выпуклое множество ![]() из действительного банахова пространства
из действительного банахова пространства ![]() в
в ![]() -мерное евклидово пространство
-мерное евклидово пространство ![]() . Пусть далее
. Пусть далее ![]() ,
,
![]() и при
и при
![]()
![]() . По
поводу других теорем о накрытии смотрите например,
. По
поводу других теорем о накрытии смотрите например, ![]() (см. теорему). Пусть
(см. теорему). Пусть ![]() столь велико, что
столь велико, что
![]() . Аналогично
вышесказанному можно показать, что на открытом шаре
. Аналогично
вышесказанному можно показать, что на открытом шаре
![]() с центром в
с центром в ![]() и радиуса
и радиуса ![]() определен
нелинейный оператор
определен
нелинейный оператор
![]() на
на ![]() . В частности, оператор
. В частности, оператор ![]() дифференцируем по Фреше
при
дифференцируем по Фреше
при ![]() ,
, ![]() и, как можно показать, при
и, как можно показать, при
![]() справедливо разложение
справедливо разложение
![]() (см. теорему) мы возьмем множество
функций
(см. теорему) мы возьмем множество
функций
![]() таких, что почти всюду на
таких, что почти всюду на ![]()
![]() . Отметим, что
. Отметим, что ![]() ,
,
![]() .
.
![]() , действующий из
, действующий из
![]() в
в ![]() по формуле (см. (25), (26))
по формуле (см. (25), (26))
![]() нам понадобится еще выражение для
нам понадобится еще выражение для
![]() в явном виде. Рассмотрим сначала случай, когда
в явном виде. Рассмотрим сначала случай, когда ![]() . Тогда
. Тогда
![\begin{eqnarray*}{c}
\lefteqn{{\cal R}_1({u(\cdot)}) = }\\ [3ex]
\displaystyle
\...
...{2} \sin \omega_1(T-s)}
\end{array}\right)
x_1^2(s)x_2(s)\, ds.
\end{eqnarray*}](img132.gif)
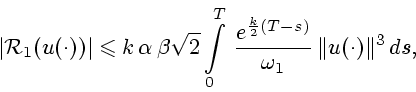
![]() (см. (28))
(см. (28))
![\begin{displaymath}
C(M, \psi) = q \int\limits^{T}_{0}
\frac{e^{\frac{k}{2}r}}{\...
...left[\,a\sin \omega_1 r + b \cos \omega_1 r\,\right]^{+}\, dr.
\end{displaymath}](img154.gif)
![]()
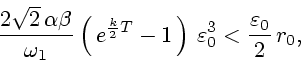
![]() и
и ![]() . В этом случае
. В этом случае
![\begin{displaymath}
\begin{array}{l}
{\cal R}_1({u(\cdot)}) = \mbox{}\\ [2ex]
\q...
..._2 (T-s)}
\end{array}\right) x_1^2(s) x_2(s)\, ds.
\end{array}\end{displaymath}](img175.gif)
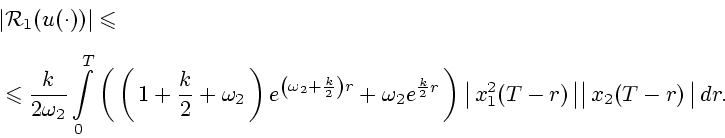
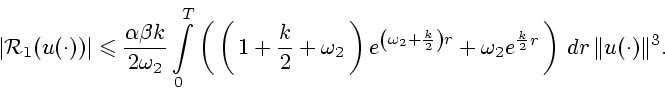
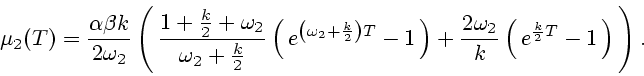
![]() , где
, где ![]() ,
анализируется с очевидными изменениями.
,
анализируется с очевидными изменениями.
![]() получаем
получаем
![\begin{displaymath}
{\cal R}_1({u(\cdot)}) = -k \int\limits^{T}_{0} e^{(T-s)} \l...
...[1ex] {1 + (T-s)}
\end{array}\right)
x_{1}^{2}(s)x_2(s)\, ds.
\end{displaymath}](img192.gif)
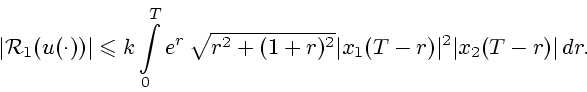
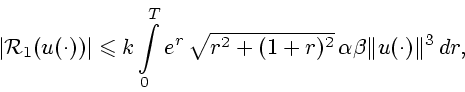
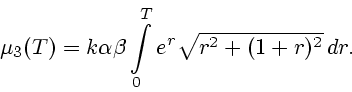
![]() . Тогда при
. Тогда при
![]() (см. (28))
(см. (28))
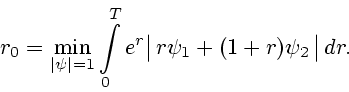
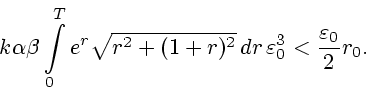
![]() рассмотреть более общий случай:
рассмотреть более общий случай:
![]() , где
, где ![]() . Но
соответствующие формулы для нахождения величины
. Но
соответствующие формулы для нахождения величины
![]() становятся
значительно сложнее по виду.
становятся
значительно сложнее по виду.