РЯД МАКЛОРЕНА ФУНКЦИИ СЕГЕ ПОЛОЖИТЕЛЬНОГО
ВЕСА, УДОВЛЕТВОРЯЮЩЕГО УСЛОВИЮ ДИНИ,
РАВНОМЕРНО СХОДИТСЯ В ЗАМКНУТОМ ЕДИНИЧНОМ
КРУГЕ1
В. М. Бадков
Аннотация:
Методами теории ортогональных многочленов доказывается теорема,
описанная в названии статьи.
Р.Салем [1] (см. также [2, стр. 323])
привел пример функции F,
принадлежащей пространству
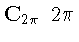 -периодических
непрерывных функций, такой, что ряд Фурье от F равномерно сходится на
-периодических
непрерывных функций, такой, что ряд Фурье от F равномерно сходится на
![$[-\pi,\pi],$](img2.gif) а ряд Фурье от F2 расходится на множестве мощности
континуума. Этот пример показывает, что композиция
а ряд Фурье от F2 расходится на множестве мощности
континуума. Этот пример показывает, что композиция
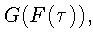 где
G - целая функция, вообще говоря, не наследует свойство равномерной
сходимости ряда Фурье функции F. Пусть
где
G - целая функция, вообще говоря, не наследует свойство равномерной
сходимости ряда Фурье функции F. Пусть  - множество
аналитических в круге
- множество
аналитических в круге
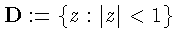 функций с равномерно
сходящимися в замкнутом круге
функций с равномерно
сходящимися в замкнутом круге 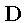 рядами Маклорена. Отвечая на
вопрос Р.Салема: существует ли
рядами Маклорена. Отвечая на
вопрос Р.Салема: существует ли
 для которой
для которой
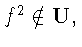 Ж.-П.Кахан и И.Кацнельсон [3] доказали существование такой
функции f. Таким образом, если G - целая функция, а
Ж.-П.Кахан и И.Кацнельсон [3] доказали существование такой
функции f. Таким образом, если G - целая функция, а
 то, вообще говоря,
то, вообще говоря,
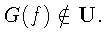 В связи с этим интересно было бы знать, для каких целых функций G и
функций f из соответствующих G подмножеств множества
В связи с этим интересно было бы знать, для каких целых функций G и
функций f из соответствующих G подмножеств множества 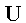 композиция
композиция
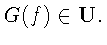 Следующая теорема, являющаяся основным
результатом этой статьи, может рассматриваться в качестве первого шага в
решении поставленной проблемы.
Следующая теорема, являющаяся основным
результатом этой статьи, может рассматриваться в качестве первого шага в
решении поставленной проблемы.
Теорема 1.Пусть (строго) положительный вес
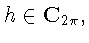 а его (равномерный) модуль непрерывности
а его (равномерный) модуль непрерывности
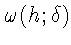 удовлетворяет условию Дини
удовлетворяет условию Дини
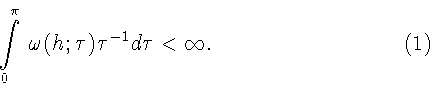
Тогда ряд Маклорена функции Сеге
равномерно сходится в замкнутом единичном круге  Доказательству этой теоремы предпошлем несколько замечаний.
Доказательству этой теоремы предпошлем несколько замечаний.
З а м е ч а н и е 1. Хорошо известно [4, стр. 268],
что равномерно сходящийся
на окружности
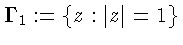 ряд, составленный из
аналитических в
ряд, составленный из
аналитических в 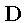 и непрерывных в
и непрерывных в
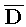 функций,
равномерно сходится в
функций,
равномерно сходится в
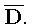 Поэтому для доказательства теоремы 1
достаточно доказать равномерную сходимость рассматриваемого в ней ряда
Маклорена функции Сеге (2) на окружности
Поэтому для доказательства теоремы 1
достаточно доказать равномерную сходимость рассматриваемого в ней ряда
Маклорена функции Сеге (2) на окружности
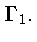
З а м е ч а н и е 2. В работе [5] автором
была установлена равномерная
сходимость на
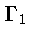 некоторой подпоследовательности сумм
Маклорена функции (2) в условиях теоремы 1.
некоторой подпоследовательности сумм
Маклорена функции (2) в условиях теоремы 1.
З а м е ч а н и е 3. Теорема 1 дает пример "хорошей"
композиции G(f(z)),
где
 наследующей
равномерную сходимость ряда Маклорена от f на
наследующей
равномерную сходимость ряда Маклорена от f на
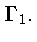 Равномерная
сходимость на
Равномерная
сходимость на
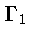 ряда Маклорена функции f указанного вида
следует из того, что функция
ряда Маклорена функции f указанного вида
следует из того, что функция
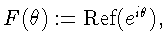 как
известно [6, стр. 25] совпадающая
почти всюду с
как
известно [6, стр. 25] совпадающая
почти всюду с
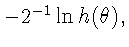 а
потому в силу (1) удовлетворяющая условию Дини
а
потому в силу (1) удовлетворяющая условию Дини
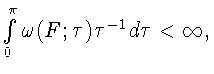 влекущему
выполнимость условия Дини-Липшица
влекущему
выполнимость условия Дини-Липшица
поскольку
Условие (3), как известно [2, стр. 280],
гарантирует равномерную сходимость
ряда Фурье функции F. Так как F удовлетворяет условию Дини, то для
сопряженной функции
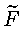 выполнено условие
выполнено условие
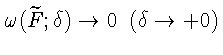 (см. [7, стр. 199, 200]),
т.е.
(см. [7, стр. 199, 200]),
т.е.
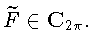 Условия
Условия
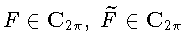 и равномерная сходимость рядя Фурье функции F влекут
равномерную сходимость ряда Фурье сопряженной функции
и равномерная сходимость рядя Фурье функции F влекут
равномерную сходимость ряда Фурье сопряженной функции
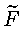 (см. [2, стр. 592]), а следовательно,
в силу соотношения
(см. [2, стр. 592]), а следовательно,
в силу соотношения
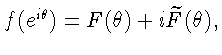 и равномерную сходимость на
и равномерную сходимость на
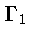 ряда Маклорена функции f.
Докажем теперь равномерную сходимость на
ряда Маклорена функции f.
Докажем теперь равномерную сходимость на
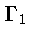 ряда Маклорена
функции (2) в условиях теоремы 1. Отсюда в силу замечания 1 будет
немедленно следовать справедливость этой теоремы.
Пусть
ряда Маклорена
функции (2) в условиях теоремы 1. Отсюда в силу замечания 1 будет
немедленно следовать справедливость этой теоремы.
Пусть
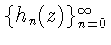 - система алгебраических
многочленов, ортонормированная на
- система алгебраических
многочленов, ортонормированная на
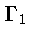 с весом h. Положим
с весом h. Положим
где Qn - алгебраический многочлен степени не выше n.
Если
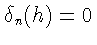 хотя бы для одного значения n, например, для
n=m, где
хотя бы для одного значения n, например, для
n=m, где
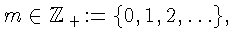 то
(см. [6, стр. 26])
то
(см. [6, стр. 26])
где
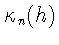 - старший коэффициент многочлена hn, а
- старший коэффициент многочлена hn, а
В этом случае доказываемое утверждение является очевидным.
Пусть теперь
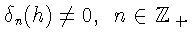 Положим
Положим
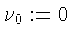 и определим рекуррентно последовательность чисел
и определим рекуррентно последовательность чисел 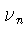 по
формуле
по
формуле
Тогда 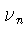 не убывает, ибо
не убывает, ибо
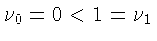 и, допустив, что
и, допустив, что
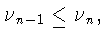 в силу (6) и невозрастания
в силу (6) и невозрастания
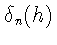 (см. (4))
имеем неравенства
(см. (4))
имеем неравенства
и, следовательно,
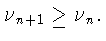 Так как
Так как
 и
и 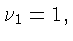 то
то
В силу монотонности 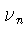 существует конечный или бесконечный
существует конечный или бесконечный
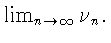 Обозначим его через A и докажем, что
Обозначим его через A и докажем, что
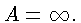 Действительно, в силу (6) хотя бы одно из равенств
Действительно, в силу (6) хотя бы одно из равенств
![$\nu_n=1+[\delta_n^{-1/2}(h)]$](img54.gif) и
и
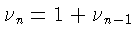 выполняется для
бесконечного числа номеров n. В обоих случаях получаем, что
выполняется для
бесконечного числа номеров n. В обоих случаях получаем, что
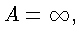 в первом - в силу того, что
в первом - в силу того, что
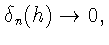 а во втором
- в силу равенства 1+A=A.
Докажем, что множество
а во втором
- в силу равенства 1+A=A.
Докажем, что множество
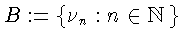 совпадает с
совпадает с
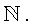 Вложение
Вложение
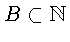 следует из (7). Так как
следует из (7). Так как 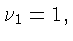 то
то 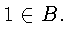 Допустим, что
Допустим, что
и
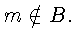 Тогда из условий
Тогда из условий 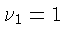 и
и
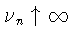 следует, что для некоторого
следует, что для некоторого
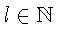 выполняются неравенства
выполняются неравенства
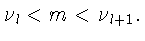 А тогда в силу (6)
А тогда в силу (6)
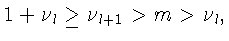 откуда и из (7) получаем, что
откуда и из (7) получаем, что
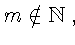 а это противоречит (8).
Итак,
а это противоречит (8).
Итак,  Разлагая многочлен
Разлагая многочлен
 по системе
по системе
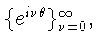 с учетом ортогональности hn с весом h
многочленам меньшей степени получаем, что
с учетом ортогональности hn с весом h
многочленам меньшей степени получаем, что
где
При 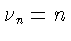 полагаем,
полагаем,
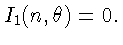 Докажем, что
Докажем, что
Принимая во внимание вытекающую из (5) формулу
получаем, что
где
Легко видеть, что
Известно, [8],[9],
что для веса h, удовлетворяющего условиям теоремы 1
Из (14)-(15) следует, что
Принимая во внимание соотношение (см. [6, стр. 25])
после замены переменной
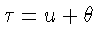 получаем формулу
получаем формулу
где
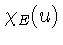 - характеристическая функция множества E. Модуль первого
из интегралов, входящих в правую часть (18), в силу (17) мажорируется
величиной
- характеристическая функция множества E. Модуль первого
из интегралов, входящих в правую часть (18), в силу (17) мажорируется
величиной
не превосходящей
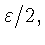 если
если 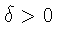 достаточно мало. При
достаточно мало. При
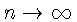 и фиксированном
и фиксированном 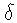 второй и третий интегралы
равномерно стремятся к нулю, так как
второй и третий интегралы
равномерно стремятся к нулю, так как
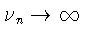 и справедлива
следующая
Лемма (см. [2, стр. 105]). Если
и справедлива
следующая
Лемма (см. [2, стр. 105]). Если
 то интегралы
то интегралы
стремятся к нулю при
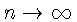 равномерно по
равномерно по
![$\theta \in [-\pi,\pi].$](img98.gif) Таким образом,
Таким образом,
Из (13), (16) и (19) вытекает (11).
Используя (9), (11), (12), заключаем, что
С другой стороны, в силу (10) и (12)
где Sn(f;z) - n-я сумма Маклорена функции f(z),
По неравенству Коши
Поскольку
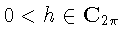 и, как известно [6, cтр. 26,
105],
и, как известно [6, cтр. 26,
105],
то правая часть (22) есть
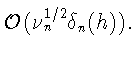 Эта
величина стремится к нулю при
Эта
величина стремится к нулю при
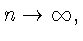 так как в силу (6) по
порядку не превосходит
так как в силу (6) по
порядку не превосходит
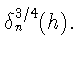 Из (20)-(22) следует, что
Из (20)-(22) следует, что
откуда с учетом (15) вытекает соотношение
Выше было показано, что
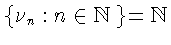 и
и
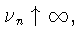 поэтому
поэтому
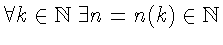 такое, что
такое, что
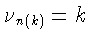 (например, можно взять
(например, можно взять
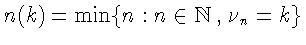 ). Отсюда в силу (23) следует предельное
соотношение
). Отсюда в силу (23) следует предельное
соотношение
означающее равномерную сходимость на 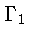 (а в силу замечания 1 -
и на
(а в силу замечания 1 -
и на
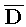 )
ряда Маклорена функции Сеге (2).
)
ряда Маклорена функции Сеге (2).
Поступила 6.06.97
![]() -периодических
непрерывных функций, такой, что ряд Фурье от F равномерно сходится на
-периодических
непрерывных функций, такой, что ряд Фурье от F равномерно сходится на
![]() а ряд Фурье от F2 расходится на множестве мощности
континуума. Этот пример показывает, что композиция
а ряд Фурье от F2 расходится на множестве мощности
континуума. Этот пример показывает, что композиция
![]() где
G - целая функция, вообще говоря, не наследует свойство равномерной
сходимости ряда Фурье функции F. Пусть
где
G - целая функция, вообще говоря, не наследует свойство равномерной
сходимости ряда Фурье функции F. Пусть ![]() - множество
аналитических в круге
- множество
аналитических в круге
![]() функций с равномерно
сходящимися в замкнутом круге
функций с равномерно
сходящимися в замкнутом круге ![]() рядами Маклорена. Отвечая на
вопрос Р.Салема: существует ли
рядами Маклорена. Отвечая на
вопрос Р.Салема: существует ли
![]() для которой
для которой
![]() Ж.-П.Кахан и И.Кацнельсон [3] доказали существование такой
функции f. Таким образом, если G - целая функция, а
Ж.-П.Кахан и И.Кацнельсон [3] доказали существование такой
функции f. Таким образом, если G - целая функция, а
![]() то, вообще говоря,
то, вообще говоря,
![]() В связи с этим интересно было бы знать, для каких целых функций G и
функций f из соответствующих G подмножеств множества
В связи с этим интересно было бы знать, для каких целых функций G и
функций f из соответствующих G подмножеств множества ![]() композиция
композиция
![]() Следующая теорема, являющаяся основным
результатом этой статьи, может рассматриваться в качестве первого шага в
решении поставленной проблемы.
Следующая теорема, являющаяся основным
результатом этой статьи, может рассматриваться в качестве первого шага в
решении поставленной проблемы.
![]() а его (равномерный) модуль непрерывности
а его (равномерный) модуль непрерывности
![]() удовлетворяет условию Дини
удовлетворяет условию Дини
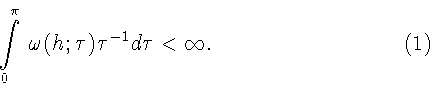
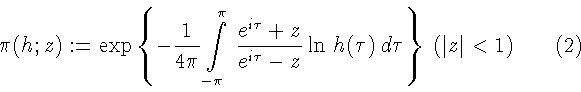
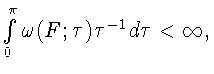 влекущему
выполнимость условия Дини-Липшица
влекущему
выполнимость условия Дини-Липшица
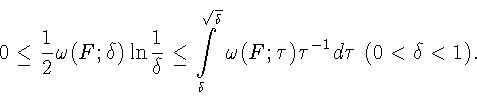
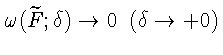 (см. [7, стр. 199, 200]),
т.е.
(см. [7, стр. 199, 200]),
т.е.
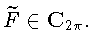 Условия
Условия
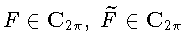 и равномерная сходимость рядя Фурье функции F влекут
равномерную сходимость ряда Фурье сопряженной функции
и равномерная сходимость рядя Фурье функции F влекут
равномерную сходимость ряда Фурье сопряженной функции
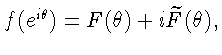 и равномерную сходимость на
и равномерную сходимость на
![\begin{displaymath}\delta_n(h):=\inf_{Q_n} \Vert [\pi(h;e^{i\tau})-Q_n(e^{i\tau})]
\sqrt{h(\tau)}\Vert _2, \eqno (4)
\end{displaymath}](img33.gif)
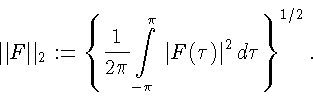
![$\nu_n=1+[\delta_n^{-1/2}(h)]$](img54.gif) и
и
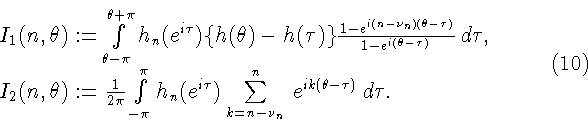
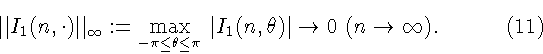
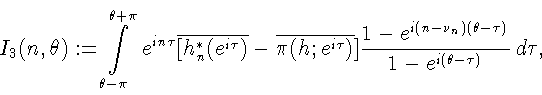
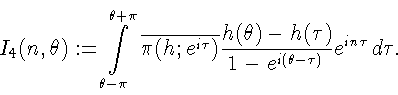
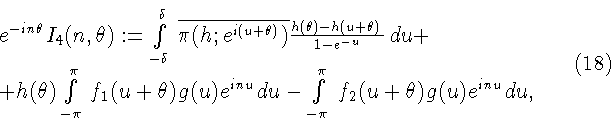
![\begin{displaymath}\begin{array}{l}
f_1(u):=\overline {\pi(h;e^{iu})},\ \ \ \
...
...-iu})^{-1}\chi_{[-\pi,\pi]/(-\delta,\delta)}(u),
\end{array}
\end{displaymath}](img88.gif)
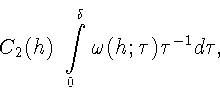

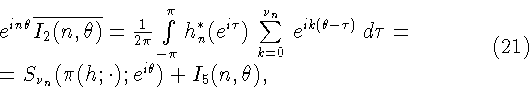
![\begin{displaymath}I_5(n,\theta):=\frac1{2\pi}\int\limits_{-\pi}^{\pi}[h_n^*(e^{...
...;e^{i\tau})]\,\sum_{k=0}^{\nu_n}\,e^{ik(\theta-\tau)}\,d\tau.
\end{displaymath}](img102.gif)
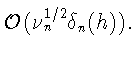 Эта
величина стремится к нулю при
Эта
величина стремится к нулю при
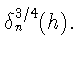 Из (20)-(22) следует, что
Из (20)-(22) следует, что