3. Асимптотический порядок точности

Из теорем 1, 2 имеем

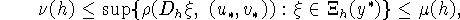
вид функций и 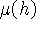указан выше.

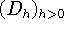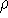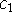Будем говорить, что алгоритм имеет -асимптотический порядок точности , если найдутся положительные константы и 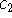такие, что при всех достаточно малых h>0 выполняются неравенства

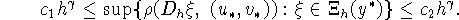
Теорема 3. Пусть выполняются условия 1, 2, 3 и выполняются согласования 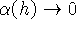,, при . Тогда КДА 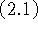- 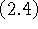имеет асимптотический порядок точности .

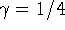Д о к а з а т е л ь с т в о. Учитывая согласования величин h, 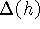, , можем записать



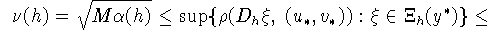
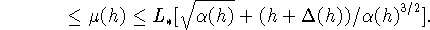
Полагая 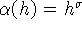, , 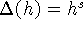получим

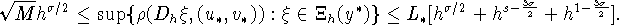
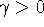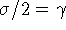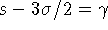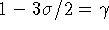Таким образом, требуется найти максимальное число , для которого , , при ограничениях 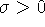, s>0. Легко определить, что 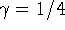при и s=1.
Теорема доказана.

Работа выполнена при поддержке Международного научного и технологического центра, грант 94-008, и Российского фонда фундаментальных исследований, грант 96-01-00846.

Поступила 15.01.96

СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ

1. Осипов Ю.С., Кряжимский А.В. О динамическом решении операторных уравнений // ДАН СССР.- 1983.- Т.269, N.3.- C.552-556.
2. Кряжимский А.В., Осипов Ю.С. О моделировании управлений в динамической системе // Изв. АН СССР. Техн. кибернетика.- 1983.- N.2. - C.51-60.
3. Osipov Yu.S. Inverse problem of dynamics for systems described by parabolic inequality.- Laxenburg, Austria, 1989.- 16p.- (Prepr./ Intern. Inst. Appl. Systems Analysis; WP-89-101).
4. Osipov Yu.S. On the reconstruction of a Parameter for a hyperbolic System.- Laxenburg, Austria, 1991.- 32p.- (Prepr./ Intern. Inst. Appl. Systems Analysis; WP-91-54).
5. Кряжимский А.В., Максимов В.И., Осипов Ю.С. О позиционном моделировании в динамических системах // Прикл. математика и механика.- 1983.- Т.47, N.6.- C.883-889.
6. Осипов Ю.С., Кряжимский А.В., Максимов В.И. Задачи динамической рагуляризации для систем с распределенными параметрами.- Свердловск, 1991. - 104c.- (Препринт ИММ УрО АН СССР).
7. Максимов В.И. О динамическом моделировании неизвестных возмущений в параболических вариационных неравенствах // Прикл. математика и механика.- 1988.- Т.52, N.5.- C.743-750.
8. Ким А.В., Короткий А.И. Динамическое моделирование возмущений в параболических системах // Изв. АН СССР. Техн. кибернетика.- 1989.- N.6.- C.78-84.
9. Ким А.В., Короткий А.И., Осипов Ю.С. Обратные задачи динамики параболических систем // Прикл. математика и механика.- 1990.- Т.54, N.5.- C.754-759.
10. Осипов Ю.С., Короткий А.И. Динамическое моделирование параметров в гиперболических системах // Изв. АН СССР. Техн. кибернетика.- 1991. - N.2.- C.154-164.
11. Osipov Yu.S., Korotkii A.I. On dynamical restoration of parameters of elliptic systems // Ill-Posed Problems in Natural Sciences- Proc. Intern. conf., Moscow, 1992.- Utrecht: VST; Moscow:TVP, 1992 P.108-117.
12. Короткий А.И., Цепелев И.А. Динамическое моделирование параметров в системе Гурса-Дарбу. // Задачи моделирования и оптимизации.- Свердловск: УрО АН СССР, 1991.- C.90-109.
13. Цепелев И.А. Конечномерная аппроксимация задачи восстановления параметров в системе Гурса-Дарбу. // Изв. РАН. Техн. кибернетика.- 1994.- N.4.- C.230-235.
14. Короткий А.И., Цепелев И.А. Динамическое решение обратной задачи определения параметров в системе Гурса-Дарбу. //Труды ИММ УрО РАН.- T.3.- C.88-103.
15. Вдовин А.Ю. Оценки точности в задаче динамического восстановления управления // Задачи позиционного моделирования: Сб. ст. / АН СССР. УНЦ.- Свердловск: УНЦ АН СССР, 1985.- C.3-11.
16. Гусев М.И., Куржанский А.Б. Обратные задачи динамики управляемых систем// Механика и науч.-техн. прогресс. Т.1: Общая и прикл. механика.- М.: Наука, 1987.- C.187-195.
17. Куржанский А.Б., Сивергина И.Ф. Метод гарантированных оценок и задачи регуляризации для эволюционных систем // Журн. вычисл. математики и мат. физики.- 1992.- N.1.- C.1720-1733.
18. Плотников В.И., Сумин В.И. Проблемы устойчивости нелинейных систем Гурса-Дарбу // Диф.уравнения.- 1972.- Т.8, N.5.- C.845-856.
19. Потапов М.М. Разностная аппроксимация и регуляризация задач оптимального управления системами Гурса-Дарбу // Вестник МГУ. Выч. матем. и кибернетика.- 1978.- N2.-C.17-26.
20. Михайлов В.П. Дифференциальные уравнения в частных производных.- М.: Наука, 1976.- 392c.